数据结构与算法之最小生成树-普林算法(Prim)/克鲁斯卡尔算法(Kruskal)
1 问题提出
1.1 一个公司计划建立一个通信网络来连接它的一个计算机中心。可以用租用的电话线连接这些中心的任何一对。应当妊娠瘙痒哪些连接,以便保证在任何两个计算机中心之间都有通路,且网络的总成本最小?可以用下较长所示的带权图为这个问题建模,其中顶点表示计算机中心,边表示可能租用的电话线,边上的权是边所表示的电话线的月租费。通过找出一棵生成树,使得这棵树的各边的权之和为最小,就可以解决这个问题。这样的生成树称为最小生成树。
1.2 最小生成树定义:在一个具有V个节点的连通无向图中,找到一个子图,该子图包含原图的所有节点和部分连接边,且不能形成回路,同时子图边的权值总和最小。
1.3 最小生成树的算法:根据对安全边的不同规则,有两种算法可以生成最小生成树。即Kruskal算法和Prim算法。
2 普林算法(Prim)图标演示
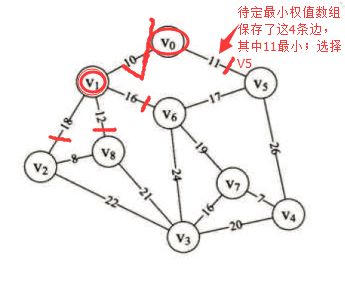
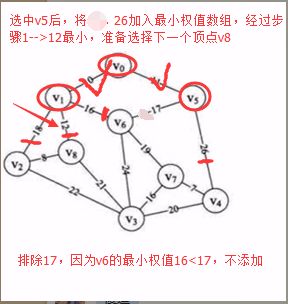
核心思想:用一个待定的最小权值的数组来保存每一个将来有可能与我们相连的临接点的最小权值,直到找到最后最小的临接点,不断的去一个一个连接
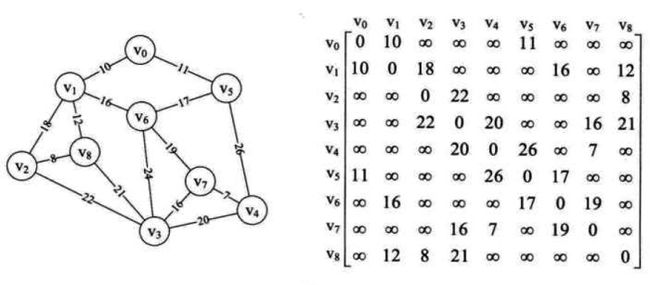
2.1 先构造邻接矩阵
2.2 lowcost分析
2.3 Java源码
package com.dn.graph.matrix;
import java.util.LinkedList;
public class Graph {
private int vertexSize;// 顶点数量
private int[] vertexs;// 顶点数组
private int[][] matrix;
private static final int MAX_WEIGHT = 1000;
private boolean[] isVisited;
public Graph(int vertextSize) {
this.vertexSize = vertextSize;
matrix = new int[vertextSize][vertextSize];
vertexs = new int[vertextSize];
for (int i = 0; i < vertextSize; i++) {
vertexs[i] = i;
}
isVisited = new boolean[vertextSize];
}
public int[] getVertexs() {
return vertexs;
}
public void setVertexs(int[] vertexs) {
this.vertexs = vertexs;
}
/**
* 获取某个顶点的出度
*
* @return
*/
public int getOutDegree(int index) {
int degree = 0;
for (int j = 0; j < matrix[index].length; j++) {
int weight = matrix[index][j];
if (weight != 0 && weight != MAX_WEIGHT) {
degree++;
}
}
return degree;
}
/**
* 获取某个顶点的入度
*/
public int getIntDegree(int index) {
int degree = 0;
for (int j = 0; j < matrix[index].length; j++) {
int weight = matrix[j][index];
if (weight != 0 && weight != MAX_WEIGHT) {
degree++;
}
}
return degree;
}
/**
* 获取两个顶点之间的权值
*
* @return
*/
public int getWeight(int v1, int v2) {
int weight = matrix[v1][v2];
return weight == 0 ? 0 : (weight == MAX_WEIGHT ? -1 : weight);
}
/**
* 获取某个顶点的第一个邻接点
*/
public int getFirstNeighbor(int index) {
for (int j = 0; j < vertexSize; j++) {
if (matrix[index][j] > 0 && matrix[index][j] < MAX_WEIGHT) {
return j;
}
}
return -1;
}
/**
* 在图中取顶点v1的在v2后的下一个邻接点
*
* @param v1表示要找的顶点
* @param v2
* 表示该顶点相对于哪个邻接点去获取下一个邻接点
*/
public int getNextNeighbor(int v, int index) {
for (int j = index + 1; j < vertexSize; j++) {
if (matrix[v][j] > 0 && matrix[v][j] < MAX_WEIGHT) {
return j;
}
}
return -1;
}
/**
* 对外公开的深度优先遍历
*/
public void depthFirstSearch() {
isVisited = new boolean[vertexSize];
for (int i = 0; i < vertexSize; i++) {
if (!isVisited[i]) {
System.out.println("访问到了:" + i + "顶点");//0
depthFirstSearch(i); // 图的深度优先遍历算法
}
}
isVisited = new boolean[vertexSize];
}
/**
* 图的深度优先遍历算法
*
* depthFirstSearch(0)开始:
* w=0,找到v0的第一个临接点v1,访问到了v1,继续depthFirstSearch(1)
* w=1,找到v1的第一个临接点v0(v0已经访问了),跳过去寻找v1的下一个临接点w=getNextNeighbor(1, 0)=2,继续while()循环
*/
private void depthFirstSearch(int i) {
isVisited[i] = true;
int w = getFirstNeighbor(i);///w=0 v0-v1 v1-v0
while (w != -1) {
if (!isVisited[w]) {
// 需要遍历该顶点
System.out.println("访问到了:" + w + "顶点");//1
depthFirstSearch(w);//w=1,找到v1的第一个临接点v0(v0已经访问了),跳过去寻找v1的下一个临接点
}
w = getNextNeighbor(i, w);// 第一个相对于w的邻接点 w=2
}
}
/**
* 对外公开的广度优先遍历
*/
public void broadFirstSearch() {
isVisited = new boolean[vertexSize];
for (int i = 0; i < vertexSize; i++) {
if (!isVisited[i]) {
broadFirstSearch(i);
}
}
}
/**
* 图的广度优先搜索算法
*
* @param i
*/
private void broadFirstSearch(int i) {
int u, w;
LinkedList queue = new LinkedList();
System.out.println("访问到:" + i + "顶点");
isVisited[i] = true;
queue.add(i);// 第一次把v0加到队列
while (!queue.isEmpty()) {
u = (Integer) (queue.removeFirst()).intValue();//出队下标
w = getFirstNeighbor(u);
while (w != -1) {
if (!isVisited[w]) {//w未被访问
System.out.println("访问到了:" + w + "顶点");
isVisited[w] = true;
queue.add(w);
}
w = getNextNeighbor(u, w);
}
}
}
/**
* prim 普里姆算法
*
*/
public void prim() {
int[] lowcost = new int[vertexSize];// 待定最小代价顶点权值的数组(为0表示已经获取最小权值)
int[] adjvex = new int[vertexSize];// 顶点下标数组
int min;//最小权值
int minId;//当前顶点下标
int sum = 0;//权值总和
//初始化第0行权值数组,作为基础数组
for (int i = 1; i < vertexSize; i++) {
lowcost[i] = matrix[0][i];
}
//遍历所有顶点
for (int i = 1; i < vertexSize; i++) {
min = MAX_WEIGHT;//初始化最小权值
minId = 0;//初始化最小权值下标(V0)
//1.查找V0余所有关联顶点的(即某一行中)最小的权值和下标,
for (int j = 1; j < vertexSize; j++) {
if (lowcost[j] < min && lowcost[j] > 0) {
min = lowcost[j];//当前的权值赋值最小权值
minId = j;//最小权值关联顶点下标(V1)
}
}
//2.赋值
System.out.println("前顶点:" + adjvex[minId] + "权值:" + min);
sum += min;//每找到一条边最小权值相加
lowcost[minId] = 0;//找到后下标置为0,代表此顶点已找到最小权值,再次遍历忽略
//3.待定的最小权值的数组保存所有当前顶点V1相连的临接点的最小权值(即某一行中与待定最小代价顶点权值的数组的值对比,小的则保存到此数组中)
for (int j = 1; j < vertexSize; j++) {
if (lowcost[j] != 0 && matrix[minId][j] < lowcost[j]) {//权值不为0,当行关联顶点权值小于对应基础数组值时
lowcost[j] = matrix[minId][j]; //修改“对应基础数组值”为当前最小关联顶点权值
adjvex[j] = minId;//修改关联顶点的“顶点下标数组值"
}
}
}
System.out.println("最小生成树权值和:" + sum);
}
public static void main(String[] args) {
Graph graph = new Graph(9);
int[] a1 = new int[] { 0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11,
MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] a2 = new int[] { 10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT,
16, MAX_WEIGHT, 12 };
int[] a3 = new int[] { MAX_WEIGHT, MAX_WEIGHT, 0, 22, MAX_WEIGHT,
MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8 };
int[] a4 = new int[] { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT,
MAX_WEIGHT, 16, 21 };
int[] a5 = new int[] { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26,
MAX_WEIGHT, 7, MAX_WEIGHT };
int[] a6 = new int[] { 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0,
17, MAX_WEIGHT, MAX_WEIGHT };
int[] a7 = new int[] { MAX_WEIGHT, 16, MAX_WEIGHT, MAX_WEIGHT,
MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT };
int[] a8 = new int[] { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7,
MAX_WEIGHT, 19, 0, MAX_WEIGHT };
int[] a9 = new int[] { MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT,
MAX_WEIGHT, MAX_WEIGHT, 0 };
graph.matrix[0] = a1;
graph.matrix[1] = a2;
graph.matrix[2] = a3;
graph.matrix[3] = a4;
graph.matrix[4] = a5;
graph.matrix[5] = a6;
graph.matrix[6] = a7;
graph.matrix[7] = a8;
graph.matrix[8] = a9;
int degree = graph.getIntDegree(4);
System.out.println("vo的入度:"+degree);
System.out.println("权值:"+graph.getWeight(7,0));
degree = graph.getOutDegree(4);
System.out.println("vo的出度:"+degree);
System.out.println("权值:"+graph.getWeight(2,3));
// graph.depthFirstSearch();
// graph.broadFirstSearch();
// graph.prim();
}
}
2.4 参考链接
最小生成树-普林算法(Prim)/克鲁斯卡尔算法(Kruskal)
Prim
最小生成树(普利姆算法、克鲁斯卡尔算法)
3 克鲁斯卡尔算法(Kruskal)图标演示
核心思想:根据边的加权值以递增的方式,一次找出加权值最低的边来构建最小生成树,而且规定:每次添加的边不能造成生成树有回路,知道找到N-1个边为止。
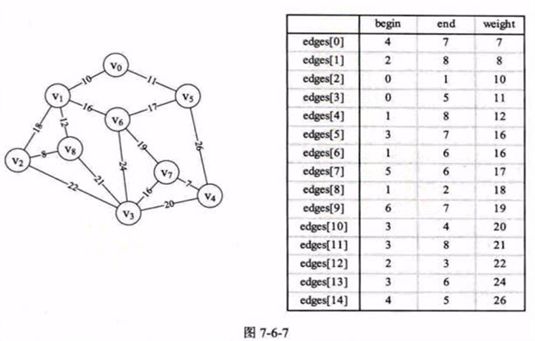
3.1 先构造邻接矩阵
3.2 打印分析
起始顶点:4---结束顶点:7~权值:7
起始顶点:2---结束顶点:8~权值:8
起始顶点:0---结束顶点:1~权值:10
找到起点0
找到终点:1 //find(0)=1
起始顶点:0---结束顶点:5~权值:11
找到起点1
找到终点:5 //find(1)=5
起始顶点:1---结束顶点:8~权值:12
起始顶点:3---结束顶点:7~权值:16
找到起点1
找到终点:5
找到起点5
找到终点:8 //find(1)=5,find(5)=8
起始顶点:1---结束顶点:6~权值:16
找到起点5
找到终点:8
找到起点8 //edges[7] 5->6=17
找到终点:6 //find(5)=8,find(8)=6 与 find(6)=6 ;所以回环
第7条边回环了
找到起点1
找到终点:5
找到起点5
找到终点:8
找到起点8
找到终点:6
找到起点2
找到终点:8
找到起点8
找到终点:6
第8条边回环了
起始顶点:6---结束顶点:7~权值:19
找到起点3
找到终点:7
找到起点4
找到终点:7
第10条边回环了
找到起点3
找到终点:7
找到起点8
找到终点:6
找到起点6
找到终点:7
第11条边回环了
找到起点2
找到终点:8
找到起点8
找到终点:6
找到起点6
找到终点:7
找到起点3
找到终点:7
第12条边回环了
找到起点3
找到终点:7
找到起点6
找到终点:7
第13条边回环了
找到起点4
找到终点:7
找到起点5
找到终点:8
找到起点8
找到终点:6
找到起点6
找到终点:7
第14条边回环了
sum:99
3.3 Java源码
package com.dn.graph.matrix;
public class GraphKruskal {
private Edge[] edges;//顶点数量
private int edgeSize;//边数量
public GraphKruskal(int edgeSize) {
this.edgeSize = edgeSize;
edges = new Edge[edgeSize];
}
/**
* Kruskal算法
*/
public void miniSpanTreeKruskal() {
int m, n, sum = 0;
int[] parent = new int[edgeSize];// 神奇的数组,下标为起点,值为终点
for (int i = 0; i < edgeSize; i++) {
parent[i] = 0;
}
for (int i = 0; i < edgeSize; i++) {
n = find(parent, edges[i].begin);//n是起点的终点
m = find(parent, edges[i].end);//m是终点的终点
if (n != m) {
parent[n] = m;
System.out.println("起始顶点:" + edges[i].begin + "---结束顶点:"+ edges[i].end + "~权值:" + edges[i].weight);
sum += edges[i].weight;
} else {
System.out.println("第" + i + "条边回环了");
}
}
System.out.println("sum:" + sum);
}
/*
* 将神奇数组进行查询获取非回环的值(下标为起点,值为终点)
*/
public int find(int[] parent, int f) {
while (parent[f] > 0) {
System.out.println("找到起点" + f);
f = parent[f];
System.out.println("找到终点:" + f);
}
return f;
}
public void createEdgeArray() {
Edge edge0 = new Edge(4, 7, 7);
Edge edge1 = new Edge(2, 8, 8);
Edge edge2 = new Edge(0, 1, 10);
Edge edge3 = new Edge(0, 5, 11);
Edge edge4 = new Edge(1, 8, 12);
Edge edge5 = new Edge(3, 7, 16);
Edge edge6 = new Edge(1, 6, 16);
Edge edge7 = new Edge(5, 6, 17);
Edge edge8 = new Edge(1, 2, 18);
Edge edge9 = new Edge(6, 7, 19);
Edge edge10 = new Edge(3, 4, 20);
Edge edge11 = new Edge(3, 8, 21);
Edge edge12 = new Edge(2, 3, 22);
Edge edge13 = new Edge(3, 6, 24);
Edge edge14 = new Edge(4, 5, 26);
edges[0] = edge0;
edges[1] = edge1;
edges[2] = edge2;
edges[3] = edge3;
edges[4] = edge4;
edges[5] = edge5;
edges[6] = edge6;
edges[7] = edge7;
edges[8] = edge8;
edges[9] = edge9;
edges[10] = edge10;
edges[11] = edge11;
edges[12] = edge12;
edges[13] = edge13;
edges[14] = edge14;
}
class Edge {
private int begin;
private int end;
private int weight;
public Edge(int begin, int end, int weight) {
super();
this.begin = begin;
this.end = end;
this.weight = weight;
}
public int getBegin() {
return begin;
}
public void setBegin(int begin) {
this.begin = begin;
}
public int getEnd() {
return end;
}
public void setEnd(int end) {
this.end = end;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
}
public static void main(String[] args) {
GraphKruskal graphKruskal = new GraphKruskal(15);
graphKruskal.createEdgeArray();
graphKruskal.miniSpanTreeKruskal();
}
}
3.4 参考链接
kruskal算法
Kruskal算法说明及图解