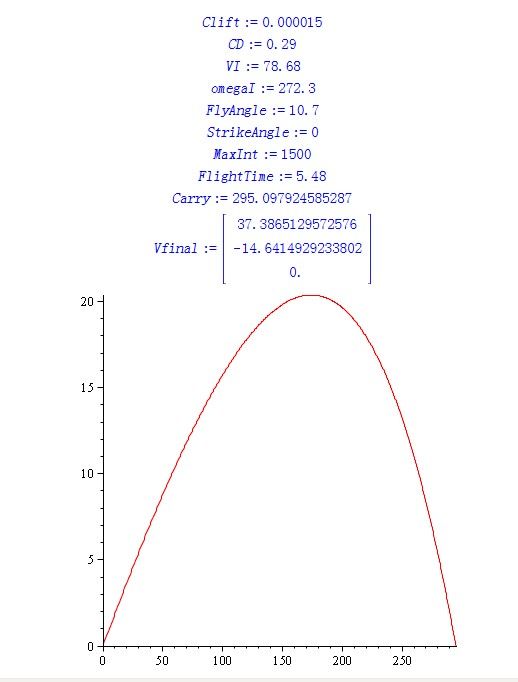
Maple学习(二)高尔夫球弹道的飞行轨迹
转载请标明是引用于 http://blog.csdn.net/chenyujing1234
源码及测试数据:
http://www.rayfile.com/zh-cn/files/05c5f00f-8609-11e1-bc82-0015c55db73d/
在做此开发之前花了半天学习Maple语言,包括Maple之程序设计、变量管理、表达式写法.....
好啦,接下来开始第一个程序之旅。
源码自己下载,这里给大家讲解源码原理。
关键技术:升力、拖力,旋转速度的算法
先看一下主函数,^-^其实Maple与Matlab的代码相当的像
#主程序循环开始
for i from 1 by 1 to MaxInt do
#根据此刻球的速度得到当前球的位置
refreshBallPos():
# 得出球的坐标,op是从表达式中抽取操作符,其实是保留Ball原来值。
Ball:=[op(Ball), [evalf(BallPosition[1]), evalf(BallPosition[2])]];
#computeFnet为此模拟建议的关键,它根据三个力算:拖力、升力、重力.算出了最终的vector力
computeFnet():
#根据力的大小得出加速度,再根据加速度得到当前速度。
refreshV(NetForce):
#更新旋转方向的速度。(这也是关键)
refreshSpin():
# 如果球到了地面,那么停止运算
if ( evalf(BallPosition[2]) < 0 ) then break end if:
end do:
#把最终变量打印出来,并显示球的轨迹图(关键的plot函数,与matlab相当像)
FlightTime:=i*deltaT;
Carry:=evalf(BallPosition[1]);
Vfinal:=evalf(V);
plot(Ball,style=LINE);
下面介绍其中一个函数computFnet() 程序过程的定义,其实的过程大家自己参考源码.
#程序的定义方法开始
> computeFnet := proc()
#声明变量
global V, omega, GravForce, B, chi, z, xi, p, k, Force, DragForce, NetForce, LiftForce,
Clift, R, CD, nu:
R:=.04267/2:
nu:=.000015:
#表软件包中装入LinearAlgebra
with(LinearAlgebra);
#拖力的计算方法一
#Force:=-alphaT*(Pi/12*p*R^2*sqrt(Pi*m/(2*KB*T))*chi*Re(z)*V-2/3*xi*Pi*R^3*m*n*
#CrossProduct(omega, V)-Pi/3*R^3*m*n*chi*Im(z)/VectorNorm(omega, 2)*
#CrossProduct(omega, CrossProduct(omega, V))):
#DragForce:=eval(Force, [alphaT=280/360, n=2.503e25, KB=1.38e-23, T=293.15,
#R=.04267/2, m=4.812e-26, kappa=.4, rho=1.1347e6, Cp=519.16]):
#拖力的计算方法二
#它适合于小精确度的模型
#CD:=4*Pi*nu/(.5-.577215665+log10(4*nu/(R*VectorNorm(V, 2)))):
#DragForce:=ScalarMultiply(V, -CD):
#拖力的计算方法三
#它适合于最基本的模型 (CD=const.)
#CD:=.29;
DragForce:=ScalarMultiply(V, -CD*R):
LiftForce:=<0,0,0>:
# 计算升力
#Clift:=.000015;
LiftForce:=Clift*CrossProduct(omega, V):
NetForce:=evalf(DragForce+GravForce+LiftForce):
end proc:
大家可以看到计算拖力有三种方法,其实高尔夫球的飞行受气流影响,因此产生了马格努斯效应,便产生了升力,
再加上球的旋转。所以计算的公式很多。在下一篇文章中会再列出其它的计算公式。
这里我取了第三种方式。
刚刚讲过建立高尔夫球模型最重要的是拖力与升力,首先是算法的选择,我也是参考了大量外面文章来对比的。
算法确定后就是系数的确定,由于高尔夫球弹道在商用的应用还是空白,所以网上资料不多,
为了得到合适的升力系数CL与拖力系数Cd,我开始了一天的偿试.
下面给大家看一下我的劳动成果吧: