bzoj 2555: SubString （LCT+后缀自动机）

2555: SubString

Time Limit: 30 Sec   Memory Limit: 512 MB
Submit: 1942   Solved: 554
[ Submit][ Status][ Discuss]

Description

  
    懒得写背景了，给你一个字符串init，要求你支持两个操作
    
    (1):在当前字符串的后面插入一个字符串
    
    (2):询问字符串s在当前字符串中出现了几次？(作为连续子串)
    
    你必须在线支持这些操作。
    

Input

    第一行一个数Q表示操作个数
    
    第二行一个字符串表示初始字符串init
    
    接下来Q行，每行2个字符串Type,Str 
    
    Type是ADD的话表示在后面插入字符串。
    
    Type是QUERY的话表示询问某字符串在当前字符串中出现了几次。
    
    为了体现在线操作，你需要维护一个变量mask，初始值为0
   
    
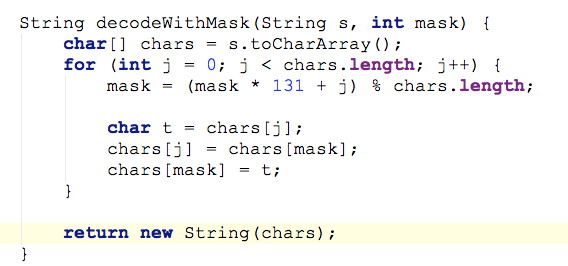
    读入串Str之后，使用这个过程将之解码成真正询问的串TrueStr。
    询问的时候，对TrueStr询问后输出一行答案Result
    然后mask = mask xor Result  
    插入的时候，将TrueStr插到当前字符串后面即可。

HINT:ADD和QUERY操作的字符串都需要解压
   

Output

Sample Input

2

A

QUERY B

ADD BBABBBBAAB

Sample Output

0

HINT

 40 % 的数据字符串最终长度 <= 20000，询问次数<= 1000，询问总长度<= 10000

    

100 % 的数据字符串最终长度 <= 600000，询问次数<= 10000,询问总长度<= 3000000

新加数据一组--2015.05.20

   

Source

Ctsc模拟赛By 洁妹

[ Submit][ Status][ Discuss]

题解：LCT+后缀自动机

这道题貌似刚开始暴力可做，但是后来又加强了数据。。。。

如果不是动态的，我们肯定考虑按照拓扑序用每个节点更新fa[i]节点，把当前节点记录的值累加给fa[i]，初值只有在主链上的点才是1.如果是动态的每次修改的，那么就是每加入一个节点，我们需要将他parent链上的所有节点记录的数量都+1，因为如果匹配到改点，他parent链上的状态都是该状态的后缀，那么都要相应的增加。

如果暴力的话每次都要遍历整条parent链，所有时间复杂度很不科学。

我们每次要修改一个点到根的链上的所有信息，并且树的形态不断改变，需要支持删边加边，我们应该很容易就想到了LCT，这些都可以用LCT来，每次的时间辅助度是O(logn).而且这道题还不用换根，所有还算比较好写。

#include
#include
#include
#include
#include
#define N 1200003
using namespace std;
int n,m,cnt,root,np,nq,p,q,last,delta[N];
int ch[N][3],fa[N],l[N],size[N],son[N][30],st[N],top,val[N],rev[N],father[N];
char s[N];
int isroot(int x)
{
	return ch[fa[x]][1]!=x&&ch[fa[x]][0]!=x;
}
int get(int x)
{
	return ch[fa[x]][1]==x;
}
void add(int x,int v)
{
	if (x) size[x]+=v,delta[x]+=v;
}
void pushdown(int x)
{
	if (delta[x]) {
		add(ch[x][0],delta[x]); add(ch[x][1],delta[x]);
		delta[x]=0;
	}
}
void rotate(int x)
{
	int y=fa[x]; int z=fa[y]; int which=get(x);
	if (!isroot(y)) ch[z][ch[z][1]==y]=x;
	ch[y][which]=ch[x][which^1]; fa[ch[x][which^1]]=y;
	ch[x][which^1]=y; fa[y]=x; fa[x]=z;
}
void splay(int x)
{
	top=0; st[++top]=x;
	for (int i=x;!isroot(i);i=fa[i])
	 st[++top]=fa[i];
	for (int i=top;i>=1;i--) pushdown(st[i]);
	while (!isroot(x)) {
		int y=fa[x];
		if (!isroot(y)) rotate(get(x)==get(y)?y:x);
		rotate(x);
	}
}
void access(int x)
{
	int t=0;
	while (x){
		splay(x);
		ch[x][1]=t; 
		t=x;
		x=fa[x];
	}
}
void link(int x,int y)
{
	fa[x]=y; 
	access(y); 
	splay(y); 
	add(y,size[x]);
}
void cut(int x)
{
	access(x); splay(x); add(ch[x][0],-size[x]);
	ch[x][0]=fa[ch[x][0]]=0;
}
void extend(int x)
{
	int c=s[x]-'A';
	p=last; np=++cnt; last=np;
	l[np]=l[p]+1; size[np]=1; 
	for (;p&&!son[p][c];p=father[p]) 
	  son[p][c]=np;
	if (!p) father[np]=root,link(np,root);
	else {
		q=son[p][c];
		if (l[q]==l[p]+1) father[np]=q,link(np,q);
		else {
			nq=++cnt; l[nq]=l[p]+1; 
			memcpy(son[nq],son[q],sizeof son[nq]);
			father[nq]=father[q]; 
			link(nq,father[q]);
			father[q]=father[np]=nq; 
			cut(q); 
			link(q,nq); 
			link(np,nq);
			for (;son[p][c]==q;p=father[p]) son[p][c]=nq;
		}
	}
}
void init(int mask)
{
	int len=strlen(s);
	for (int i=0;i