归并排序算法的过程图解
- 归并排序
- 1 你会学到什么
- 2 讨论的问题是什么
- 3 相关的概念和理论
- 4 归并排序过程详解
- 归并简介
- 二路归并
- 二路归并演示
- 总体思路
- 完整例子
- 5 算法评价
- 6 总结
- 欢迎关注算法channel公众号
归并排序
归并排序是分而治之思想的典型应用。
1 你会学到什么?
彻底弄明白常用的排序算法的基本思想,算法的时间和空间复杂度,以及如何选择这些排序算法,确定要解决的问题的最佳排序算法,已经总结了冒泡排序和其改进后的快速排序算法,直接选择排序和堆排序算法,总结了直接插入排序到希尔排序做的改进,下面总结归并排序。
2 讨论的问题是什么?
各种排序算法的基本思想;讨论各种排序算法的时间、空间复杂度;以及算法的稳定性;算法是如何改进的,比如冒泡排序如何改进成了目前最常用的快速排序的,直接选择排序到堆排序的改进,直接插入排序到希尔排序做的优化,下面讨论归并排序。
3 相关的概念和理论
内部排序
若整个排序过程不需要访问外存便能完成,则称此类排序问题为内部排序。
外部排序
若参加排序的记录数量很大,整个序列的排序过程不可能在内存中完成,则称此类排序问题为外部排序。
就地排序
若排序算法所需的辅助空间并不依赖于问题的规模n,即辅助空间为O(1),称为就地排序。
稳定排序
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序后,这些记录的相对次序保持不变,即在原序列中 ri=rj, ri 在 rj 之前,而在排序后的序列中,ri 仍在 rj 之前,则称这种排序算法是稳定的;否则称为不稳定的。
排序序列分布
排序需要考虑待排序关键字的分布情况,这会影响对排序算法的选择,通常我们在分析下列算法时都考虑关键字分布是随机分布的,不是按照某种规律分布的,比如正态分布等。
待排序序列
排序序列中,剩余即将要排序的序列部分。
已排序序列
排序序列中,已经排序好的序列部分。
4 归并排序过程详解
归并简介
归并排序,英文名称是MERGE-SORT。
它是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。
算法的核心概念—二路归并
若将两个有序表合并成一个有序表,称为二路归并。
二路归并
比较 a[i] 和 b[j] 的大小,若 a[i]≤b[j],则将第一个有序表中的元素a[i]复制到 r[k] 中,并令i 和 k 分别加上1;否则将第二个有序表中的元素b[j]复制到r[k] 中,并令 j 和 k 分别加上1;
如此循环下去,直到其中一个有序表取完;
然后再将另一个有序表中剩余的元素复制到 r 中从下标 k 到下标t的单元。
这个过程,请见下面的例子演示。
二路归并演示
如下图所示,初始状态时,a序列[2,3,5]和b序列[2,9]为已排序好的子序列,现在利用二路归并,将a和b合并为有序序列 r,初始时,i指向a的第一个元素,j指向b的第一个元素,k初始值等于0。
说明,r中最后一个元素起到哨兵的作用,灰色显示。

第一步,比较a[i]和b[j],发现相等,如果规定相等时,a的先进入r,则如下图所示,i, k分别加1,为了形象化,归并后的元素不再绘制。

第二步,继续比较,此时b[j]小,所以b的元素2进入r,则如下图所示,j, k分别加1,

第三步,继续比较,此时a[i]小,所以a的元素3进入r,则如下图所示,i, k分别加1,

第四步,继续比较,此时a[i]小,所以a的元素5进入r,则如下图所示,i, k分别加1,此时序列a的3个元素已经归并完,b中还剩下一个,这个可以通过k可以看出,它还没有到达个数5。

第五步,将序列b中的所有剩余元素直接放入r中即可,不用做任何比较了,直至b变空,二路归并结束。
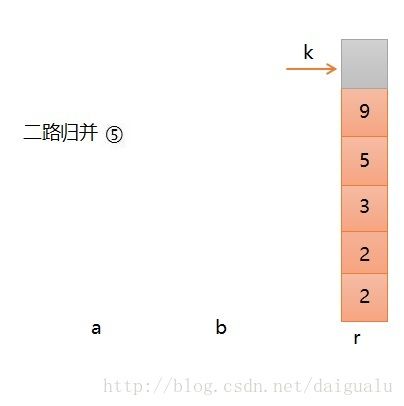
总体思路
归并排序的算法我们通常用递归实现。
先把待排序区间 [s,t] 以中点二分;
接着把左边子区间排序;
再把右边子区间排序;
最后把左区间和右区间用一次归并操作合并成有序的区间 [s,t] 。
完整例子
我们仍然用冒泡排序和其改进后的快速排序算法,直接选择排序和堆排序算法,直接插入排序到希尔排序做的改进这三篇中用到的待排序列
3 2 5 9 2
伪代码
sort(unsorted, start, end, sorted)
{
if(start<end) {
mid = start + (end-start)/2; //分隔区间
sort(unsorted, start,mid,sorted);
sort(unsorted,mid+1,end,sorted);
merge(unsorted,start,mid,end,sorted);
}
}过程模拟
下图演示的是归并排序递归版,第一次执行二路归并时的示意图,注意观察右图的栈的入栈顺序,可以看到sort的入栈顺序,当执行一次merge时,一定是有2个sort返回并有序了,如下图,sort[0,0]和sort[1,1](递归返回的条件是start

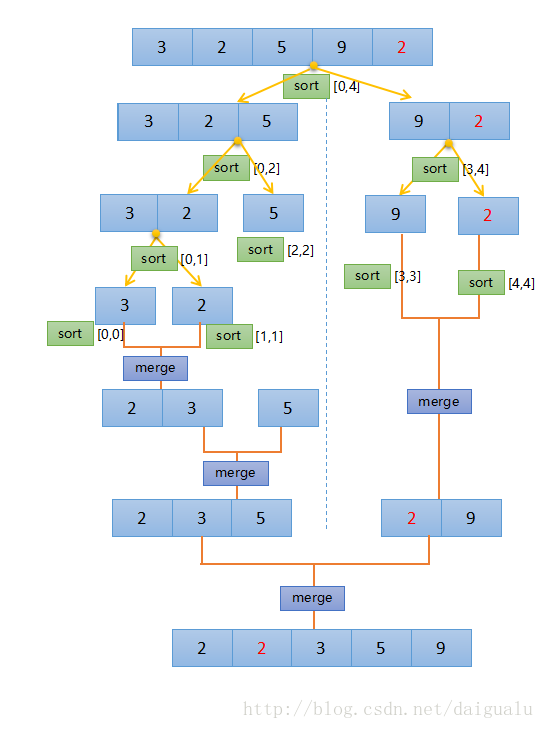
如下为上个例子的归并排序的完整示例,sort 和 merge 的示意图,可以看到最后一次merge,正是上面说到的二路 [2,3,5] 和 [2,9] 的归并排序,如果不熟的,可以回过头再看看。
5 算法评价
归并排序的时间复杂度为O(nlogn) ,因为递归每次按照一半分区,并且merge需要线性时间。最重要的是该算法中最好、最坏和平均的时间性能都是O(nlogn)。
归并排序的空间复杂度为O(n),会占用内存。
总之,归并排序虽然比较占用内存,但却是一种效率高且稳定的算法。
6 总结
归并排序的时间复杂度,在最坏,最好和平均都是O(nlogn),这是效率,性能非常好的排序算法。
只不过它需要占用 O(n)的内存空间,如果数据量一旦很大,内存可能吃不消,这是它的弱点和致命伤。而其他排序算法,比如快速排序,希尔排序,都是就地排序算法,它们不占用额外的内存空间。
不过,这个占用内存的弱点,可以改进为就地排序,大家感兴趣,可以查看一下。
更多排序算法原理过程解读
冒泡排序和其改进后的快速排序算法
直接选择排序和堆排序算法
直接插入排序到希尔排序做的改进
欢迎关注《算法channel》公众号
