王家林人工智能AI 第七节课：四种性能优化Matrix编写AI框架实战（Gradient Descent的陷阱、及几种常见的性能优化方式实战）老师微信13928463918

王家林人工智能AI 第七节课：四种性能优化Matrix编写AI框架实战（Gradient Descent的陷阱、及几种常见的性能优化方式实战）老师微信13928463918

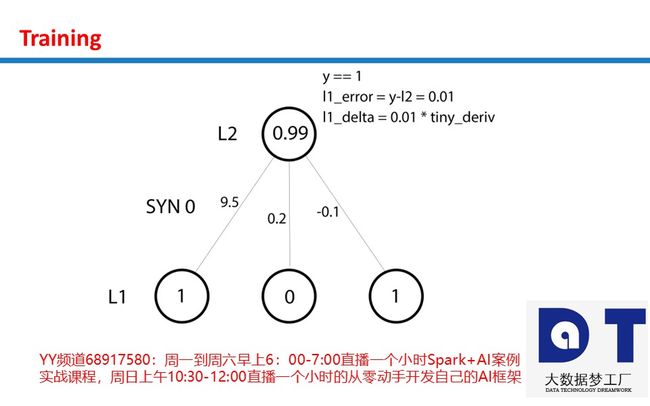
     在上一节课从零起步(无需数学和Python基础)编码实现AI框架之第六节课：使用Matrix编写AI框架实战及测试（https://blog.csdn.net/duan_zhihua/article/details/80041548）中，我们实现了一个简单的反向传播的神经网络。

    (本文根据家林大神课程及相关网络资料整理。)

先看一个代码：

import numpy as np
X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])
y = np.array([[0,1,1,0]]).T
alpha,hidden_dim = (0.5,4)
synapse_0 = 2*np.random.random((3,hidden_dim)) - 1
synapse_1 = 2*np.random.random((hidden_dim,1)) - 1
for j in xrange(60000):
    layer_1 = 1/(1+np.exp(-(np.dot(X,synapse_0))))
    layer_2 = 1/(1+np.exp(-(np.dot(layer_1,synapse_1))))
    layer_2_delta = (layer_2 - y)*(layer_2*(1-layer_2))
    layer_1_delta = layer_2_delta.dot(synapse_1.T) * (layer_1 * (1-layer_1))
    synapse_1 -= (alpha * layer_1.T.dot(layer_2_delta))
    synapse_0 -= (alpha * X.T.dot(layer_1_delta))

一、优化

    反向传播让我们可以测量网络中的每项权重对总误差的贡献，我们可以使用很多不同的非线性优化方法对反向传播进行优化：

• • • •  Annealing（退火）
      • Stochastic Gradient Descent（随机梯度下降）
      • AW-SGB
      • Momentum (SGD)（动量）
      • Nesterov Momentum (SGD)（Nesterov动量）
      • AdaGrad
      • AdaDelta
      • ADAM
      • BFGS
      • LBFGS

可视化优化方法的差异
ConvNet.js(http://cs.stanford.edu/people/karpathy/convnetjs/demo/trainers.html)

RobertsDionne(http://www.robertsdionne.com/bouncingball/)

这些优化算法在不同的场景下表现良好，在某些场景下，我们可以同时使用多个优化算法。本节课讨论梯度下降。梯度下降是最简单、应用最广泛的神经网络优化算法。

二、梯度下降

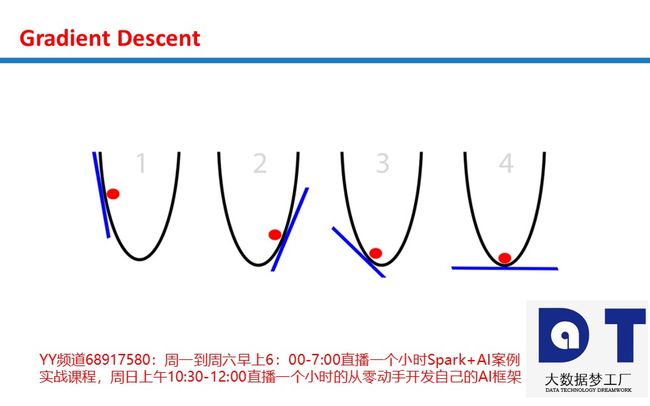
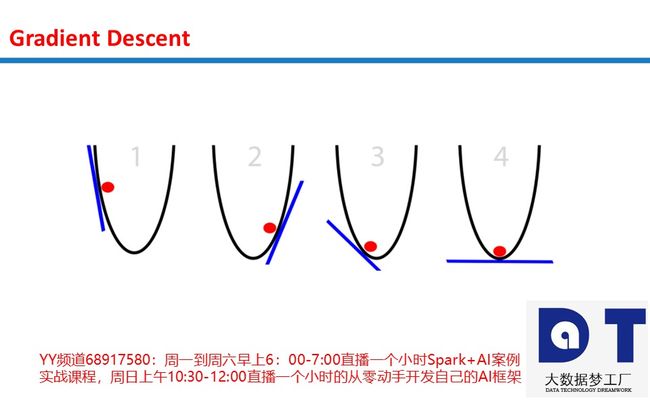
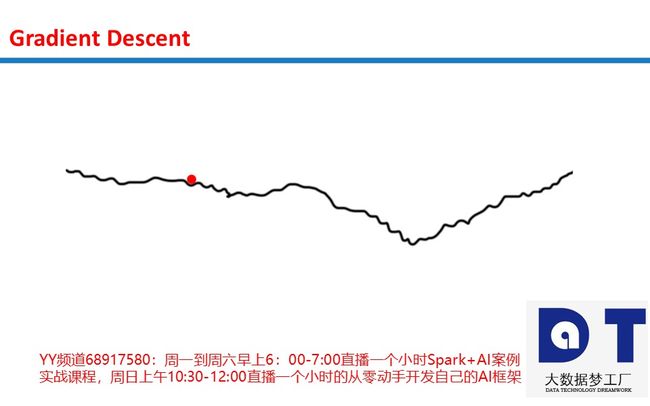
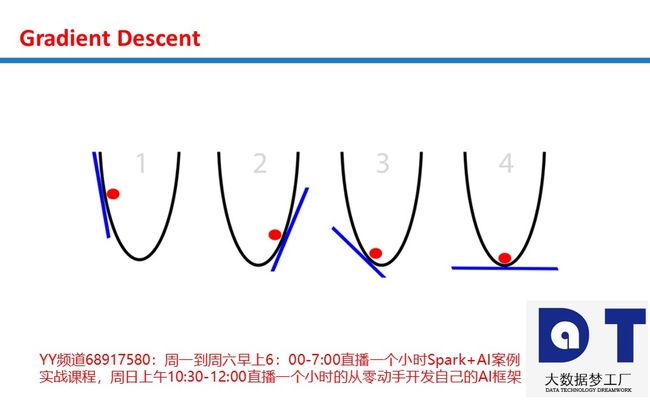
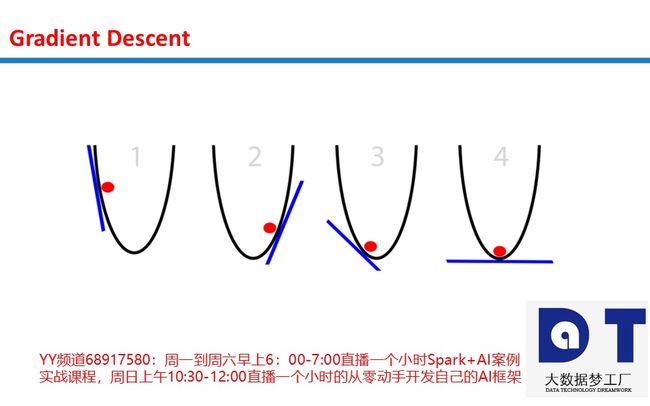
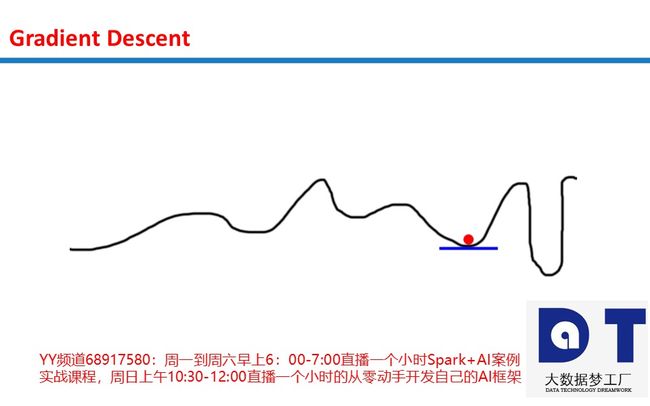
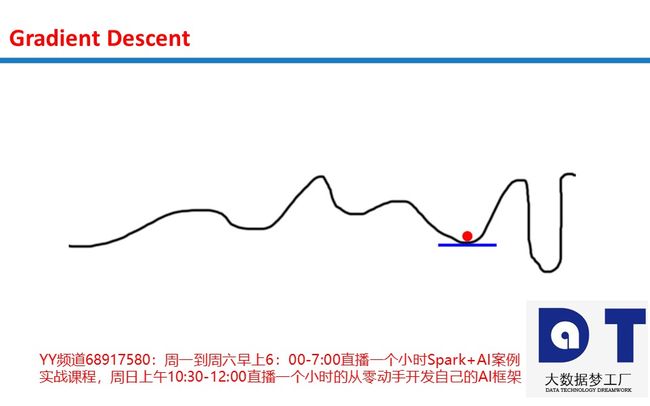
想象一个圆筐中的红球试图找到筐底，这就是优化（optimization）。在这个例子中，球优化它的位置以寻找筐的最低点。 

我们可以把这看成一个游戏：球有两个选项，向左，或是向右。目标：使自己的位置尽可能地低。

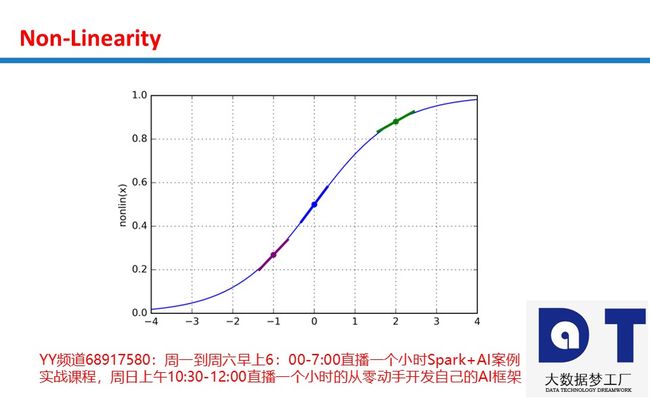
        那么，球是基于什么信息调整自己的位置来找到最低点的呢？根据斜率（slope）来确定，即下图中的蓝线。注意，当斜率（slope）为负时（左高右低，从左自右往下），球应该向右移动。而当斜率（slope）为正时（左低右高，从右自左往下），球应该向左。根据这些信息足以让球在几次迭代之后找到筐底。这是优化的一个子领域，称为梯度优化（gradient optimization）。 

过于简化的梯度下降

• 在当前位置计算斜率（slope）
• 如果斜率（slope）为负，向右移动
• 如果斜率（slope）为正，向左移动
• （重复这一过程，直到梯度为零）

有一个问题，每次球需要移动多长的距离？看看球筐，斜率（slope）越陡，球离底部的距离越远。这很有用！让我们利用这一新信息改进我们的算法。同时，我们假设筐在一个(x,y)平面上。因此，球的位置为x，增加x意味着向右移动，减少x意味着向左移动。

朴素梯度下降

• 计算当前位置x的斜率（slope）
• 从x减去斜率（x = x - 斜率）
• （重复这一过程，直到斜率为零）

 可以在脑海中想象这一过程。对我们的算法而言，这是一个可观的改善。对较大的正斜率，我们向左移动较长的距离。对很小的正斜率，我们向左移动很短的距离。随着球越来越接近底部，球每次移动的距离越来越短，直到斜率为零，球停在这一点上。这个停止的点称为收敛（convergence）。

三、可能的问题

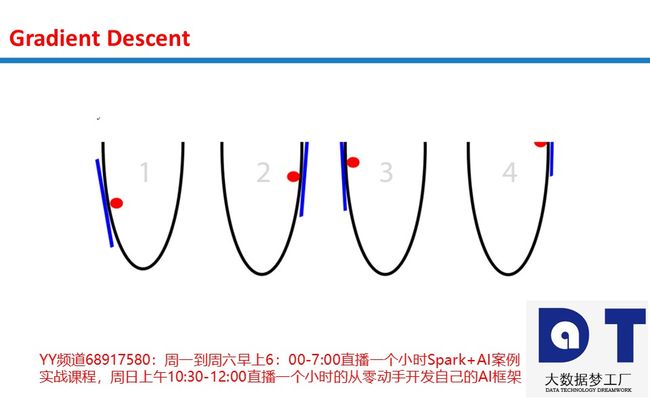
问题一：斜率（slope）过大，多大算过大？ 步幅取决于斜率（slope）的陡峭程度。有时斜率（slope）过陡，我们的移动过头了很多。稍微有点移动过头没问题，但有时我们过头到了比开始的时候离底部更远的程度！

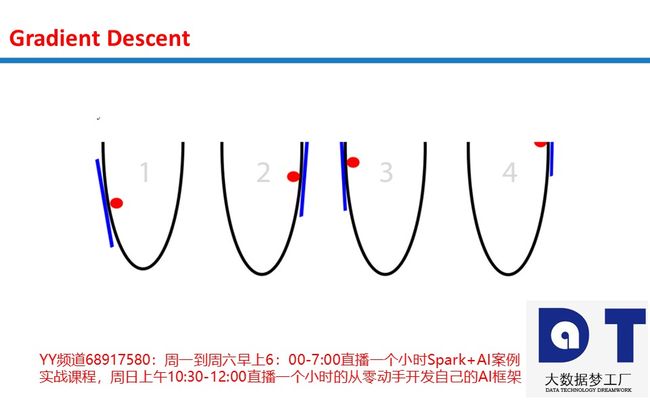
让这个坑极具破坏性的一点是过头到了这种程度，意味着我们将落在相反反向上更陡峭的斜坡上。这将使我们再次移动过头，并且过头得更厉害。这一移动过头的恶性循环称为发散（divergence）。

解决方案一：让斜率小一点
     每个神经网络都大量使用这一技巧。如果我们的梯度过大，我们让它小一点！我们给梯度（所有梯度）乘上一个0到1之间的系数（比如0.01）。这个小数通常是一个称为alpha的单精度浮点数。如此做了之后，就不会过头了，网络也可以收敛了。

 梯度下降改进版

• alpha = 0.1 （或0到1之间的某个数）
• 计算当前位置x的斜率
• x = x - alpha * 斜率
• （重复这一过程，直到斜率为零）

问题二：局部极小值

有时筐的形状很有趣，沿着坡度无法让你到达绝对最低点。

这是目前为止梯度下降最大的坑。有无数尝试绕过这个坑的办法。一般而言，它们多多少少都依靠某种随机搜索方法在筐的不同部分尝试。

解决方案二：多个随机开始状态

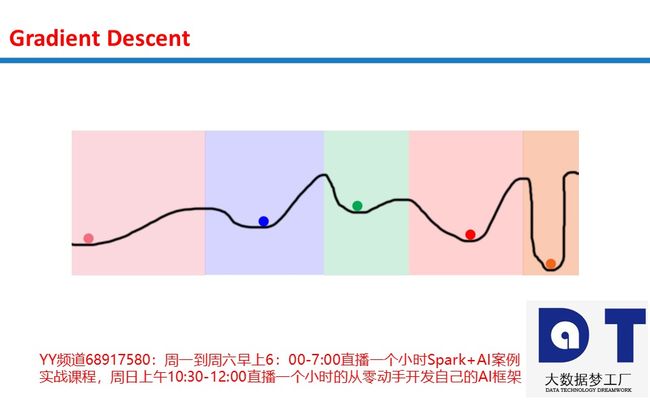
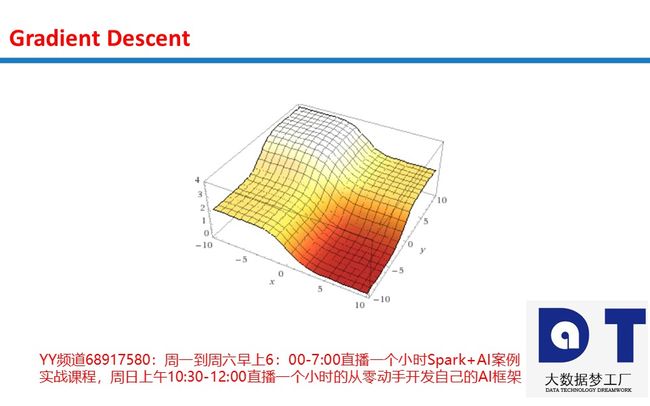
有无数通过随机性绕过这个坑的方法。这提出了一个问题，如果我们需要通过随机性来查找全局最小值，为什么我们一开始要优化？为什么不直接随机地尝试呢？下图给出了答案。

想象一下，我们在上图中随机放置100个球，然后开始优化。最终所有的球都会落在5个位置上（上图5个颜色不同的球所在的位置）。着色的区域表示每个局部极小值的领域。例如，蓝色领域内随机放置的球会收敛至蓝色极小值。这意味着，我们只需随机搜索5个空间，就可以搜索整个空间！这比纯随机搜索要好太多了，纯随机搜索需要尝试所有空间（取决于粒度，这可能意味着几百万个空间）。

在神经网络中： 神经网络做到这一点的其中一个方式是使用很大的隐藏层。层中的每个隐藏节点从不同的随机状态开始。这让每个隐藏节点收敛到网络的不同模式。参数化这一尺寸让网络使用者可以选择尝试单个神经网络中数千（甚至是数百亿）个不同的局部极小值。

旁注一： 这正是神经网络如此强大的原因！ 神经网络具备搜索比实际计算多得多的空间的能力！（理论上）我们可以仅仅使用5个球和不多的迭代搜索上图中的整条黑线。以暴力破解的方式搜索同一空间需要多很多数量级的计算。

旁注二： 仔细观察的人可能会问：“好，为什么我们让这么多节点收敛至同一点？这不是在浪费算力吗？”这是一个很好的问题。当前最先进的避免隐藏节点给出相同答案（通过搜索同一个空间）的方法是Dropout和Drop-Connect  。

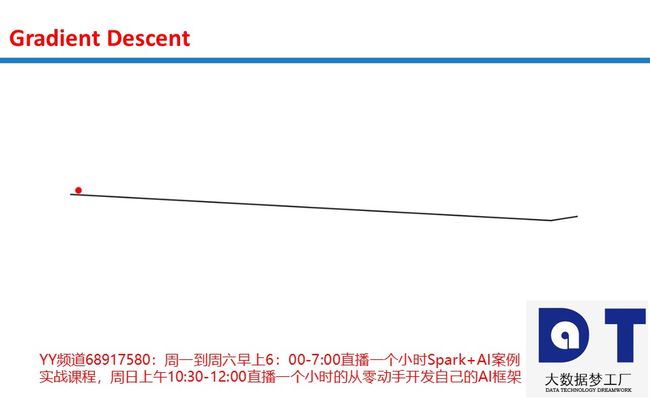
问题三：坡度过小
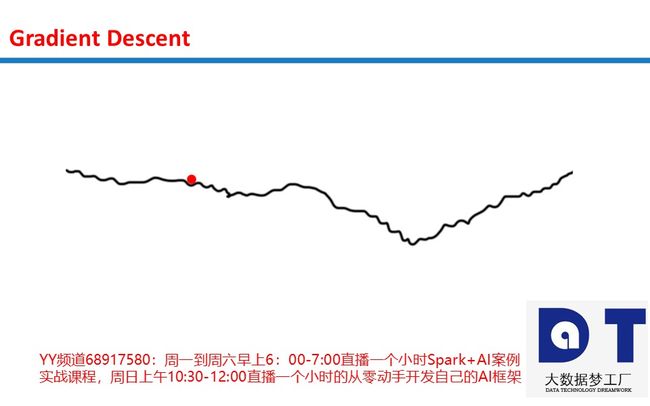
神经网络有时会落入坡度过小的坑。答案同样是显然的。考虑下面的图形。

我们的小红球陷入了困境！如果我们的alpha太小，就可能出现这种情况。球落入了附近的局部极小值而忽略了整个图形。它不具备打破日复一日的乏味生活的精力（umph）。

增量过小更明显的一个症状也许是收敛需要花很长很长的时间。

解决方案三：增加alpha

如同你可能期望的一样，增加alpha可以对付这两个症状。我们甚至可以给增量乘上一个大于1的权重。这很罕见，但有时我们确实需要这么做。

四、神经网络中的SGD

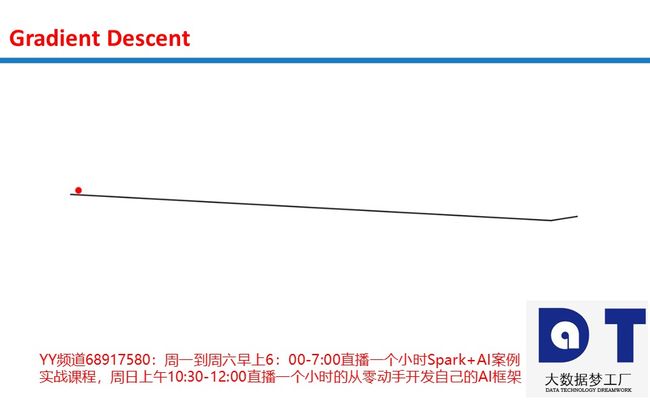
到了这一步，你可能想知道，这和神经网络还有反向传播有什么关系？这是最难的部分

看到上图中的曲线没有？在神经网络中，我们试图最小化对应权重的误差。所以，那条曲线代表对应于单个权重的位置的网络误差。因此，如果我们为单个权重的每个可能值计算网络误差，就得到了上图中的曲线。接着我们将选中具有最小误差（曲线的最低点）的单个权重的值。我说单个权重是因为这是一个二维图形。所以，x维是权重的值，而y维是权重在此位置时神经网络的误差。

双层神经网络：

import numpy as np

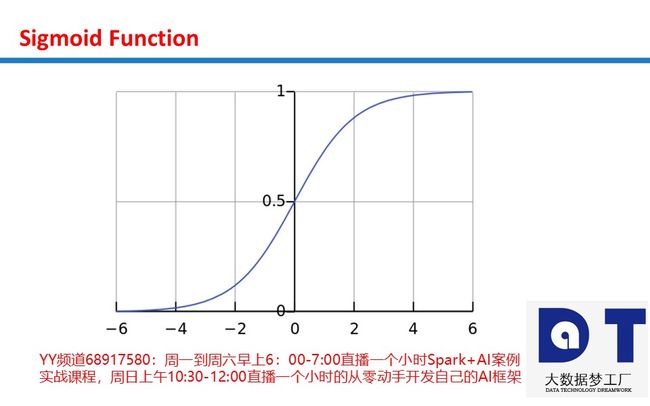
# compute sigmoid nonlinearity
def sigmoid(x):
    output = 1/(1+np.exp(-x))
    return output

# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
    return output*(1-output)
    
# input dataset
X = np.array([  [0,1],
                [0,1],
                [1,0],
                [1,0] ])
    
# output dataset            
y = np.array([[0,0,1,1]]).T

# seed random numbers to make calculation
# deterministic (just a good practice)
np.random.seed(1)

# initialize weights randomly with mean 0
synapse_0 = 2*np.random.random((2,1)) - 1

for iter in xrange(10000):

    # forward propagation
    layer_0 = X
    layer_1 = sigmoid(np.dot(layer_0,synapse_0))

    # how much did we miss?
    layer_1_error = layer_1 - y

    # multiply how much we missed by the 
    # slope of the sigmoid at the values in l1
    layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)
    synapse_0_derivative = np.dot(layer_0.T,layer_1_delta)

    # update weights
    synapse_0 -= synapse_0_derivative

print "Output After Training:"
print layer_1

在这个例子中，我们在输出处有一个单一的误差（单个值），我们在第35行计算了这一误差。由于我们有两个权重，因此输出的“误差平面”是一个三维空间。我们可以将这看成一个(x,y,z)平面，其中z轴为误差，x和y是syn0中两个权重的值。

让我们尝试一下绘制上面的网络/数据集的这一误差平面，看看会是什么样的。所以，我们如何计算给定权重集合的误差呢？第31、32、35行代码展示了答案。如果我们绘制对应每个可能的权重集合（x和y在-10到10之间）的总误差（表示网络在整个数据集上的误差的单个标量），它看起来是这样的。

这其实很简单，不过是计算所有可能的权重集合，然后对应每个集合的网络误差而已。如你所见，我们的输出数据和第一个输入数据正相关。因此，当x（synapse_0的第一个权重）很大时，误差最小化。那么，请思考一下，synapse_0的第二个权重的情况是什么样的？它是何时达到最优的呢？

我们的双层神经网络如何优化：好，既然第31、32、35行计算误差，第39、40、43行自然就优化减少误差了。这是梯度下降发生的地方！

朴素梯度下降

• 第39、40行： 计算当前位置x的斜率
• 第43行：从x减去斜率（x = x - 斜率）
• 第28行：（重复这一过程，直到斜率为零）
• 这完全是一回事！唯一改变的是我们有2个权重，所以我们优化2个权重而不是1个。不过，逻辑是完全一样的。

五、改进我们的网络

改进一：增加并调优alpha参数
什么是alpha？ 如上所述，alpha参数以最简单的方式降低每次迭代更新的幅度。在更新权重前的最后时刻，我们将权重更新乘以alpha（通常位于0到1之间，从而降低权重更新的幅度）。这一微小的代码改动对训练能力绝对有巨大的影响。 在合适的地方加上alpha参数。接着，我们将运行一系列试验，用alpha参数在实际代码中的表现印证我们发展的所有关于alpha的直觉。

梯度下降改进版

• 计算当前位置x的斜率
• 第56、57行： x = x - alpha * 斜率
• （重复这一过程，直到斜率为零）

import numpy as np

alphas = [0.001,0.01,0.1,1,10,100,1000]

# compute sigmoid nonlinearity
def sigmoid(x):
    output = 1/(1+np.exp(-x))
    return output

# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
    return output*(1-output)
    
X = np.array([[0,0,1],
            [0,1,1],
            [1,0,1],
            [1,1,1]])
                
y = np.array([[0],
			[1],
			[1],
			[0]])

for alpha in alphas:
    print "\nTraining With Alpha:" + str(alpha)
    np.random.seed(1)

    # randomly initialize our weights with mean 0
    synapse_0 = 2*np.random.random((3,4)) - 1
    synapse_1 = 2*np.random.random((4,1)) - 1

    for j in xrange(60000):

        # Feed forward through layers 0, 1, and 2
        layer_0 = X
        layer_1 = sigmoid(np.dot(layer_0,synapse_0))
        layer_2 = sigmoid(np.dot(layer_1,synapse_1))

        # how much did we miss the target value?
        layer_2_error = layer_2 - y

        if (j% 10000) == 0:
            print "Error after "+str(j)+" iterations:" + str(np.mean(np.abs(layer_2_error)))

        # in what direction is the target value?
        # were we really sure? if so, don't change too much.
        layer_2_delta = layer_2_error*sigmoid_output_to_derivative(layer_2)

        # how much did each l1 value contribute to the l2 error (according to the weights)?
        layer_1_error = layer_2_delta.dot(synapse_1.T)

        # in what direction is the target l1?
        # were we really sure? if so, don't change too much.
        layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)

        synapse_1 -= alpha * (layer_1.T.dot(layer_2_delta))
        synapse_0 -= alpha * (layer_0.T.dot(layer_1_delta))

Training With Alpha:0.001
Error after 0 iterations:0.496410031903
Error after 10000 iterations:0.495164025493
Error after 20000 iterations:0.493596043188
Error after 30000 iterations:0.491606358559
Error after 40000 iterations:0.489100166544
Error after 50000 iterations:0.485977857846

Training With Alpha:0.01
Error after 0 iterations:0.496410031903
Error after 10000 iterations:0.457431074442
Error after 20000 iterations:0.359097202563
Error after 30000 iterations:0.239358137159
Error after 40000 iterations:0.143070659013
Error after 50000 iterations:0.0985964298089

Training With Alpha:0.1
Error after 0 iterations:0.496410031903
Error after 10000 iterations:0.0428880170001
Error after 20000 iterations:0.0240989942285
Error after 30000 iterations:0.0181106521468
Error after 40000 iterations:0.0149876162722
Error after 50000 iterations:0.0130144905381

Training With Alpha:1
Error after 0 iterations:0.496410031903
Error after 10000 iterations:0.00858452565325
Error after 20000 iterations:0.00578945986251
Error after 30000 iterations:0.00462917677677
Error after 40000 iterations:0.00395876528027
Error after 50000 iterations:0.00351012256786

Training With Alpha:10
Error after 0 iterations:0.496410031903
Error after 10000 iterations:0.00312938876301
Error after 20000 iterations:0.00214459557985
Error after 30000 iterations:0.00172397549956
Error after 40000 iterations:0.00147821451229
Error after 50000 iterations:0.00131274062834

Training With Alpha:100
Error after 0 iterations:0.496410031903
Error after 10000 iterations:0.125476983855
Error after 20000 iterations:0.125330333528
Error after 30000 iterations:0.125267728765
Error after 40000 iterations:0.12523107366
Error after 50000 iterations:0.125206352756

Training With Alpha:1000
Error after 0 iterations:0.496410031903
Error after 10000 iterations:0.5
Error after 20000 iterations:0.5
Error after 30000 iterations:0.5
Error after 40000 iterations:0.5
Error after 50000 iterations:0.5

我们从不同大小的alpha中观察到了什么？
Alpha = 0.001
这样一个alpha小得的网络差点不能收敛！这是因为我们所做的权重更新如此之小，以至于我们基本上没有改变什么，即使是在60000次迭代之后！这是一个教科书般的例子：问题三 坡度过小。

Alpha = 0.01
这个alpha值达成了一个相当不错的收敛。在60000次迭代的过程中，它收敛的过程很平滑，但最终不如另一些alpha收敛得好。这仍然是一个教科书般的例子：问题三 坡度过小。

Alpha = 0.1
这个alpha值非常迅速地取得了一些进展，不过接着进展就要慢一些。仍然是因为问题三。我们需要加大一点alpha。

Alpha = 1
聪明的读者大概已经想到了，这和没有alpha的收敛效果一样！权重更新乘以1，什么都没有改变。

Alpha = 10
也许你会惊讶，一个大于1的alpha值仅仅在10000次迭代后就取得了比其他alpha值的最终结果都要好的分数！这告诉我们，基于较小alpha的权重更新过于保守了。也就是说，基于较小的alpha值时，网络的权重基本上朝着正确的方向走，只不过它们需要加快一点速度。

Alpha = 100
现在我们可以看到，步幅过大会适得其反。网络的步子迈得太大，以至于无法在误差平面上找到一个合理的低点。这是一个教科书般的问题一的例子。alpha过大，因此它只是在误差平面上跳来跳去，永远不会安心地呆在局部极小值处。

Alpha = 1000
一个极端巨大的alpha让我们看到了一个发散的教科书般的例子，误差不降反增……硬化于0.5. 这是一个更极端的问题一的例子，它横冲直撞，结果欲速则不达，最后离任何局部极小值都很远。

让我们仔细看看

import numpy as np

alphas = [0.001,0.01,0.1,1,10,100,1000]

# compute sigmoid nonlinearity
def sigmoid(x):
    output = 1/(1+np.exp(-x))
    return output

# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
    return output*(1-output)
    
X = np.array([[0,0,1],
            [0,1,1],
            [1,0,1],
            [1,1,1]])
                
y = np.array([[0],
			[1],
			[1],
			[0]])



for alpha in alphas:
    print "\nTraining With Alpha:" + str(alpha)
    np.random.seed(1)

    # randomly initialize our weights with mean 0
    synapse_0 = 2*np.random.random((3,4)) - 1
    synapse_1 = 2*np.random.random((4,1)) - 1
        
    prev_synapse_0_weight_update = np.zeros_like(synapse_0)
    prev_synapse_1_weight_update = np.zeros_like(synapse_1)

    synapse_0_direction_count = np.zeros_like(synapse_0)
    synapse_1_direction_count = np.zeros_like(synapse_1)
        
    for j in xrange(60000):

        # Feed forward through layers 0, 1, and 2
        layer_0 = X
        layer_1 = sigmoid(np.dot(layer_0,synapse_0))
        layer_2 = sigmoid(np.dot(layer_1,synapse_1))

        # how much did we miss the target value?
        layer_2_error = y - layer_2

        if (j% 10000) == 0:
            print "Error:" + str(np.mean(np.abs(layer_2_error)))

        # in what direction is the target value?
        # were we really sure? if so, don't change too much.
        layer_2_delta = layer_2_error*sigmoid_output_to_derivative(layer_2)

        # how much did each l1 value contribute to the l2 error (according to the weights)?
        layer_1_error = layer_2_delta.dot(synapse_1.T)

        # in what direction is the target l1?
        # were we really sure? if so, don't change too much.
        layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)
        
        synapse_1_weight_update = (layer_1.T.dot(layer_2_delta))
        synapse_0_weight_update = (layer_0.T.dot(layer_1_delta))
        
        if(j > 0):
            synapse_0_direction_count += np.abs(((synapse_0_weight_update > 0)+0) - ((prev_synapse_0_weight_update > 0) + 0))
            synapse_1_direction_count += np.abs(((synapse_1_weight_update > 0)+0) - ((prev_synapse_1_weight_update > 0) + 0))        
        
        synapse_1 += alpha * synapse_1_weight_update
        synapse_0 += alpha * synapse_0_weight_update
        
        prev_synapse_0_weight_update = synapse_0_weight_update
        prev_synapse_1_weight_update = synapse_1_weight_update
    
    print "Synapse 0"
    print synapse_0
    
    print "Synapse 0 Update Direction Changes"
    print synapse_0_direction_count
    
    print "Synapse 1"
    print synapse_1

    print "Synapse 1 Update Direction Changes"
    print synapse_1_direction_count

Training With Alpha:0.001
Error:0.496410031903
Error:0.495164025493
Error:0.493596043188
Error:0.491606358559
Error:0.489100166544
Error:0.485977857846
Synapse 0
[[-0.28448441  0.32471214 -1.53496167 -0.47594822]
 [-0.7550616  -1.04593014 -1.45446052 -0.32606771]
 [-0.2594825  -0.13487028 -0.29722666  0.40028038]]
Synapse 0 Update Direction Changes
[[ 0.  0.  0.  0.]
 [ 0.  0.  0.  0.]
 [ 1.  0.  1.  1.]]
Synapse 1
[[-0.61957526]
 [ 0.76414675]
 [-1.49797046]
 [ 0.40734574]]
Synapse 1 Update Direction Changes
[[ 1.]
 [ 1.]
 [ 0.]
 [ 1.]]

Training With Alpha:0.01
Error:0.496410031903
Error:0.457431074442
Error:0.359097202563
Error:0.239358137159
Error:0.143070659013
Error:0.0985964298089
Synapse 0
[[ 2.39225985  2.56885428 -5.38289334 -3.29231397]
 [-0.35379718 -4.6509363  -5.67005693 -1.74287864]
 [-0.15431323 -1.17147894  1.97979367  3.44633281]]
Synapse 0 Update Direction Changes
[[ 1.  1.  0.  0.]
 [ 2.  0.  0.  2.]
 [ 4.  2.  1.  1.]]
Synapse 1
[[-3.70045078]
 [ 4.57578637]
 [-7.63362462]
 [ 4.73787613]]
Synapse 1 Update Direction Changes
[[ 2.]
 [ 1.]
 [ 0.]
 [ 1.]]

Training With Alpha:0.1
Error:0.496410031903
Error:0.0428880170001
Error:0.0240989942285
Error:0.0181106521468
Error:0.0149876162722
Error:0.0130144905381
Synapse 0
[[ 3.88035459  3.6391263  -5.99509098 -3.8224267 ]
 [-1.72462557 -5.41496387 -6.30737281 -3.03987763]
 [ 0.45953952 -1.77301389  2.37235987  5.04309824]]
Synapse 0 Update Direction Changes
[[ 1.  1.  0.  0.]
 [ 2.  0.  0.  2.]
 [ 4.  2.  1.  1.]]
Synapse 1
[[-5.72386389]
 [ 6.15041318]
 [-9.40272079]
 [ 6.61461026]]
Synapse 1 Update Direction Changes
[[ 2.]
 [ 1.]
 [ 0.]
 [ 1.]]

Training With Alpha:1
Error:0.496410031903
Error:0.00858452565325
Error:0.00578945986251
Error:0.00462917677677
Error:0.00395876528027
Error:0.00351012256786
Synapse 0
[[ 4.6013571   4.17197193 -6.30956245 -4.19745118]
 [-2.58413484 -5.81447929 -6.60793435 -3.68396123]
 [ 0.97538679 -2.02685775  2.52949751  5.84371739]]
Synapse 0 Update Direction Changes
[[ 1.  1.  0.  0.]
 [ 2.  0.  0.  2.]
 [ 4.  2.  1.  1.]]
Synapse 1
[[ -6.96765763]
 [  7.14101949]
 [-10.31917382]
 [  7.86128405]]
Synapse 1 Update Direction Changes
[[ 2.]
 [ 1.]
 [ 0.]
 [ 1.]]

Training With Alpha:10
Error:0.496410031903
Error:0.00312938876301
Error:0.00214459557985
Error:0.00172397549956
Error:0.00147821451229
Error:0.00131274062834
Synapse 0
[[ 4.52597806  5.77663165 -7.34266481 -5.29379829]
 [ 1.66715206 -7.16447274 -7.99779235 -1.81881849]
 [-4.27032921 -3.35838279  3.44594007  4.88852208]]
Synapse 0 Update Direction Changes
[[  7.  19.   2.   6.]
 [  7.   2.   0.  22.]
 [ 19.  26.   9.  17.]]
Synapse 1
[[ -8.58485788]
 [ 10.1786297 ]
 [-14.87601886]
 [  7.57026121]]
Synapse 1 Update Direction Changes
[[ 22.]
 [ 15.]
 [  4.]
 [ 15.]]

Training With Alpha:100
Error:0.496410031903
Error:0.125476983855
Error:0.125330333528
Error:0.125267728765
Error:0.12523107366
Error:0.125206352756
Synapse 0
[[-17.20515374   1.89881432 -16.95533155  -8.23482697]
 [  5.70240659 -17.23785161  -9.48052574  -7.92972576]
 [ -4.18781704  -0.3388181    2.82024759  -8.40059859]]
Synapse 0 Update Direction Changes
[[  8.   7.   3.   2.]
 [ 13.   8.   2.   4.]
 [ 16.  13.  12.   8.]]
Synapse 1
[[  9.68285369]
 [  9.55731916]
 [-16.0390702 ]
 [  6.27326973]]
Synapse 1 Update Direction Changes
[[ 13.]
 [ 11.]
 [ 12.]
 [ 10.]]

Training With Alpha:1000
Error:0.496410031903
Error:0.5
Error:0.5
Error:0.5
Error:0.5
Error:0.5
Synapse 0
[[-56.06177241  -4.66409623  -5.65196179 -23.05868769]
 [ -4.52271708  -4.78184499 -10.88770202 -15.85879101]
 [-89.56678495  10.81119741  37.02351518 -48.33299795]]
Synapse 0 Update Direction Changes
[[ 3.  2.  4.  1.]
 [ 1.  2.  2.  1.]
 [ 6.  6.  4.  1.]]
Synapse 1
[[  25.16188889]
 [  -8.68235535]
 [-116.60053379]
 [  11.41582458]]
Synapse 1 Update Direction Changes
[[ 7.]
 [ 7.]
 [ 7.]
 [ 3.]]

在以上代码中，对导数改变方向的次数进行了计数（训练结束后的“Update Direction Changes”）。如果斜率slope（导数）改变了方向，那意味着它越过了局部极小值，需要回退。如果它从未改变方向，那么很可能它走得不够远。

几点总结：

• alpha很小时，导数几乎从不改变方向。
• alpha最优时，导数多次改变方向。
  
• alpha很大时，导数改变方向的次数中等。
• alpha很小时，最终权重也很小。
• alpha很大时，权重也变得很大。

改进二：参数化隐藏层的尺寸

能够增加隐藏层的话，可以增加每次迭代收敛的搜索空间数量。

import numpy as np

alphas = [0.001,0.01,0.1,1,10,100,1000]
hiddenSize = 32

# compute sigmoid nonlinearity
def sigmoid(x):
    output = 1/(1+np.exp(-x))
    return output

# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
    return output*(1-output)
    
X = np.array([[0,0,1],
            [0,1,1],
            [1,0,1],
            [1,1,1]])
                
y = np.array([[0],
			[1],
			[1],
			[0]])

for alpha in alphas:
    print "\nTraining With Alpha:" + str(alpha)
    np.random.seed(1)

    # randomly initialize our weights with mean 0
    synapse_0 = 2*np.random.random((3,hiddenSize)) - 1
    synapse_1 = 2*np.random.random((hiddenSize,1)) - 1

    for j in xrange(60000):

        # Feed forward through layers 0, 1, and 2
        layer_0 = X
        layer_1 = sigmoid(np.dot(layer_0,synapse_0))
        layer_2 = sigmoid(np.dot(layer_1,synapse_1))

        # how much did we miss the target value?
        layer_2_error = layer_2 - y

        if (j% 10000) == 0:
            print "Error after "+str(j)+" iterations:" + str(np.mean(np.abs(layer_2_error)))

        # in what direction is the target value?
        # were we really sure? if so, don't change too much.
        layer_2_delta = layer_2_error*sigmoid_output_to_derivative(layer_2)

        # how much did each l1 value contribute to the l2 error (according to the weights)?
        layer_1_error = layer_2_delta.dot(synapse_1.T)

        # in what direction is the target l1?
        # were we really sure? if so, don't change too much.
        layer_1_delta = layer_1_error * sigmoid_output_to_derivative(layer_1)

        synapse_1 -= alpha * (layer_1.T.dot(layer_2_delta))
        synapse_0 -= alpha * (layer_0.T.dot(layer_1_delta))

Training With Alpha:0.001
Error after 0 iterations:0.496439922501
Error after 10000 iterations:0.491049468129
Error after 20000 iterations:0.484976307027
Error after 30000 iterations:0.477830678793
Error after 40000 iterations:0.46903846539
Error after 50000 iterations:0.458029258565

Training With Alpha:0.01
Error after 0 iterations:0.496439922501
Error after 10000 iterations:0.356379061648
Error after 20000 iterations:0.146939845465
Error after 30000 iterations:0.0880156127416
Error after 40000 iterations:0.065147819275
Error after 50000 iterations:0.0529658087026

Training With Alpha:0.1
Error after 0 iterations:0.496439922501
Error after 10000 iterations:0.0305404908386
Error after 20000 iterations:0.0190638725334
Error after 30000 iterations:0.0147643907296
Error after 40000 iterations:0.0123892429905
Error after 50000 iterations:0.0108421669738

Training With Alpha:1
Error after 0 iterations:0.496439922501
Error after 10000 iterations:0.00736052234249
Error after 20000 iterations:0.00497251705039
Error after 30000 iterations:0.00396863978159
Error after 40000 iterations:0.00338641021983
Error after 50000 iterations:0.00299625684932

Training With Alpha:10
Error after 0 iterations:0.496439922501
Error after 10000 iterations:0.00224922117381
Error after 20000 iterations:0.00153852153014
Error after 30000 iterations:0.00123717718456
Error after 40000 iterations:0.00106119569132
Error after 50000 iterations:0.000942641990774

Training With Alpha:100
Error after 0 iterations:0.496439922501
Error after 10000 iterations:0.5
Error after 20000 iterations:0.5
Error after 30000 iterations:0.5
Error after 40000 iterations:0.5
Error after 50000 iterations:0.5

Training With Alpha:1000
Error after 0 iterations:0.496439922501
Error after 10000 iterations:0.5
Error after 20000 iterations:0.5
Error after 30000 iterations:0.5
Error after 40000 iterations:0.5
Error after 50000 iterations:0.5

注意到32节点的最佳误差为0.0009，而4隐藏节点的最佳误差为0.0013. 这看起来没有相差很多，但这是重要的一课。我们只需要3个节点就足以表示这个数据集。然而，因为我们开始搜索的时候有更多的节点，我们可以在每次迭代中搜索更多空间，最终收敛得更快。尽管在这一玩具问题中，这一效应显得微不足道，当我们建模非常复杂的数据集时，这一效应将起到非常大的作用。

六、结语和以后的工作

如果你对神经网络的态度是严肃的，那有一个建议，自己编码实现这个网络。这也许听起来有点疯狂，但它切切实实很有帮助。如果你希望能够根据最新的学术论文创建任意的神经网络架构，或者阅读和理解不同架构的代码样例，这是一个杀手级练习。即使你使用Torch、Caffe、Theano之类的框架，这仍是有用的。 

如果你打算进一步改进你的网络，下面是一些值得了解的概念。

• Bias Units（偏置单元）
• Mini-Batches
• Delta Trimming
• Parameterized Layer Sizes（参数化的层尺寸）
• Regularization（正则化）
• Dropout
• Momentum（动量）
• Batch Normalization
• GPU兼容性
• 其他酷炫特性

家林大神授课的四种性能优化Matrix编写AI框架实战 从（ANN_V1.py -ANN_V6.py）演化迭代改进六个版本的代码示意图

3980元团购原价19800元的AI课程，团购请加王家林老师微信13928463918

基于王家林老师独创的人工智能“项目情景投射”学习法，任何IT人员皆可在无需数学和Python语言的基础上的情况下3个月左右的时间成为AI技术实战高手:

1，五节课（分别在4月9-13号早上YY视频直播）教你从零起步(无需Python和数学基础)开发出自己的AI深度学习框架，五节课的学习可能胜过你五年的自我摸索；

2，30个真实商业案例代码中习得AI(从零起步到AI实战专家之路)：10大机器学习案例、13大深度学习案例、7大增强学习案例(本文档中有案例的详细介绍和案例实现代码截图)；

3，100天的涅槃蜕变，平均每天学习1个小时(周一到周六早上6:00-7:00YY频道68917580视频直播)，周末复习每周的6个小时的直播课程(报名学员均可获得所有的直播视频、全部的商业案例完整代码、最具阅读价值的AI资料等)。

五节课从零起步(无需数学和Python基础)编码实现AI人工智能框架电子书V1
https://download.csdn.net/download/duan_zhihua/10380279

30个真实商业案例代码中成为AI实战专家(10大机器学习案例、13大深度学习案例、7大增强学习案例)课程大纲
https://download.csdn.net/download/duan_zhihua/10366665

数统治着宇宙。——毕达哥拉斯