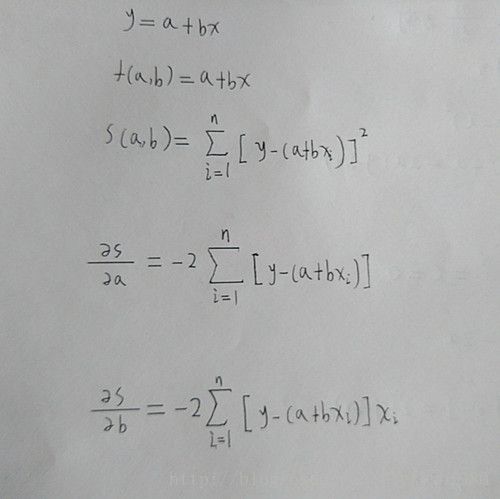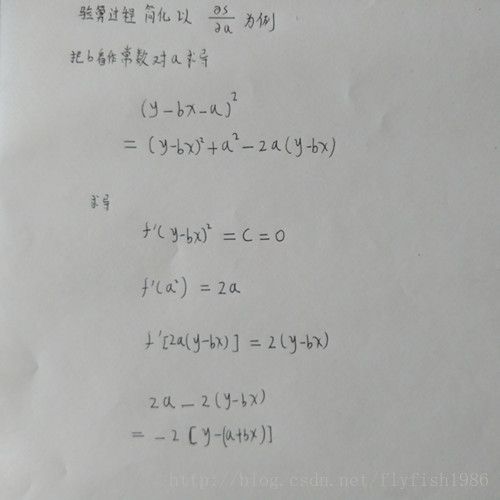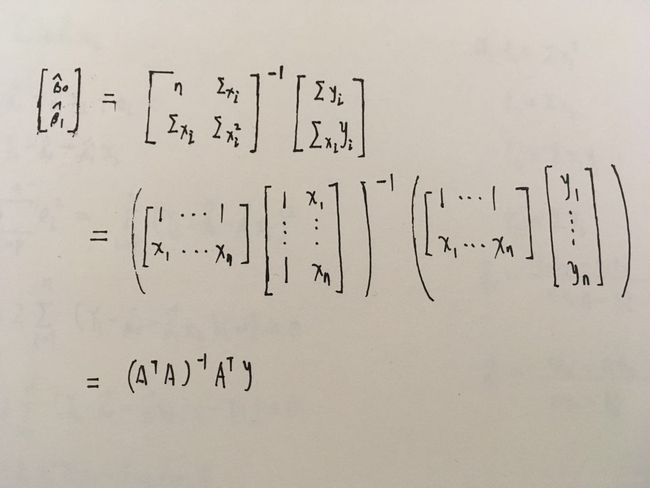TensorFlow - 最小二乘法

TensorFlow - 最小二乘法

flyfish

以y = ax + b 举例画图
图中 a和b已知

假设有如下，x和y的值，选取最合适的a, b，让该等式”尽量成立”, 从而找出最优解

y = ax+b 中
x,y的值是
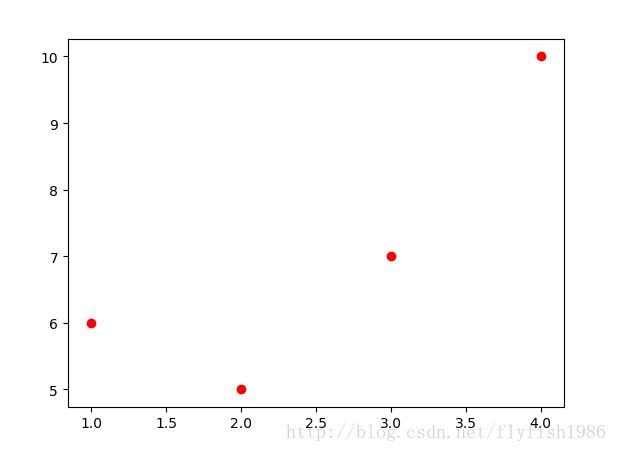
(1,6)
(2,5)
(3,7)
(4,10)

a+1b=6
a+2b=5
a+3b=7
a+4b=10

S(a,b)=[6−(a+1b)]2+[5−(a+2b)]2+[7−(a+3b)]2+[10−(a+4b)]2=4a2+30b2+20ab−56a−154b+210.

∂S∂a=0=8a+20b−56

∂S∂b=0=20a+60b−154.

解得
a = 3.5
b = 1.4

求偏导数例子

推导

验算过程

矩阵方式
Ax+By=C

A1x+B1y=C1,
A2x+B2y=C2,

矩阵表示
(A1B1A2B2)(xy)=(C1C2).

Ax=b

minx∈Rn∥Ax−b∥2

解释
∥x∥=|x| x的绝对值

∥x∥2:=x21+⋯+x2n−−−−−−−−−−√.

minx∈Rn∥Ax−b∥22

∥Ax−b∥22=(Ax−b)T∗(Ax−b)

T的含义 矩阵转置
⎡⎣⎢1,23,45,6⎤⎦⎥T=[1,3,52,4,6]

#include "stdafx.h"
#include
#include
using namespace std;

struct point
{
    double x;
    double y;

};
class LeastSquares
{
private:
    double a, b;
public:
    LeastSquares(std::vector& p)
    {
        int n = p.size();
        double t1 = 0, t2 = 0, t3 = 0, t4 = 0;
        for (int i = 0; i < n; i++)
        {
            t1 = t1 + (p[i].x * p[i].x);
            t2 = t2 + p[i].x;
            t3 = t3 + (p[i].x * p[i].y);
            t4 = t4 + p[i].y;
        }
        a = (t3*n - t2*t4) / (t1*n - t2*t2);
        b = (t1*t4 - t2*t3) / (t1*n - t2*t2);
    }
    void output() const
    {
        std::cout << "y = " << a << "x + " << b << "\n";
    }
};
int main()
{
    std::vector p{ {1,6},{2,5},{3,7},{4,10} };
    LeastSquares ls(p);
    ls.output();
    system("pause");

    return 0;
}
// y= a*x + b; 输出 y=1.4x+3.5 

TensorFlow的一个例子

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

#start stop number
x1 = np.linspace(1,100) #从1到100之间默认产生50个数
x2 = np.linspace(1,10,10)#从1到10之间产生10个数
x3 = np.random.randn(3, 4) #正态分布中返回3列数据，
#print(x1)
#print(x2)
#print(x3)

num_examples = 50
X = np.array([np.linspace(-2, 4, num_examples), np.linspace(-6, 6, num_examples)])

#2行50列数据
X += np.random.randn(2, num_examples)
x, y = X

#print(X.shape);#(2,50)
#print(x);#第一行数据 x是-2, 4之间产生50个数
#print(y);#第二行数据 y是-6, 6之间产生50个数
#print(np.transpose([y]));

#构建 50行，2列的数组，第一列都是1
x_with_bias = np.array([(1., a) for a in x]).astype(np.float32)
#print(x_with_bias.shape)# (50,2) 行数和列数

losses = []
training_steps = 50
learning_rate = 0.002

with tf.Session() as sess:
    # Set up all the tensors, variables, and operations.
    input = tf.constant(x_with_bias)

    #矩阵转置 一行50列，变成50行1列
    target = tf.constant(np.transpose([y]).astype(np.float32))

    # an interface that takes a tuple as the first argument
    #2行1列
    #tf.random_normal(shape, mean=0.0, stddev=1.0, dtype=tf.float32, seed=None, name=None)
    weights = tf.Variable(tf.random_normal([2, 1], 0, 0.1))


    tf.global_variables_initializer().run()

    '''
    #tf.matmul(a, b, transpose_a=False, transpose_b=False, a_is_sparse=False, b_is_sparse=False, name=None)

    # 2-D tensor `a`
    a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3])
    # [[1. 2. 3.]
    # [4. 5. 6.]]

    # 2-D tensor `b`
    b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2])
    # [[7. 8.]
    # [9. 10.]
    # [11. 12.]]
    c = tf.matmul(a, b) 
    # [[58 64]
    #  [139 154]]
    '''
    yhat = tf.matmul(input, weights)

    #减法  tf.subtract(10, 4) # 6
    yerror = tf.subtract(yhat, target)


    '''  
    tf.nn.l2_loss(t, name=None)

    L2 Loss.

    Computes half the L2 norm of a tensor without the sqrt:

    output = sum(t ** 2) / 2
    Args:

    t: A Tensor. Must be one of the following types: float32, float64, int64, int32, uint8, int16, int8, complex64, qint8, quint8, qint32. Typically 2-D, but may have any dimensions.
    name: A name for the operation (optional).
    Returns:

    A Tensor. Has the same type as t. 0-D.
    '''

    loss = tf.nn.l2_loss(yerror)

    #梯度下降法 梯度下降法是求解最小二乘问题的一种迭代法
    update_weights = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

    for _ in range(training_steps):
        # Repeatedly run the operations, updating the TensorFlow variable.
        update_weights.run()
        losses.append(loss.eval())

    # Training is done, get the final values for the graphs
    betas = weights.eval()
    yhat = yhat.eval()

    #print(weights.shape);
    #print(weights.eval());

# Show the fit and the loss over time.
fig, (ax1, ax2) = plt.subplots(1, 2)
plt.subplots_adjust(wspace=.3)
fig.set_size_inches(10, 4)
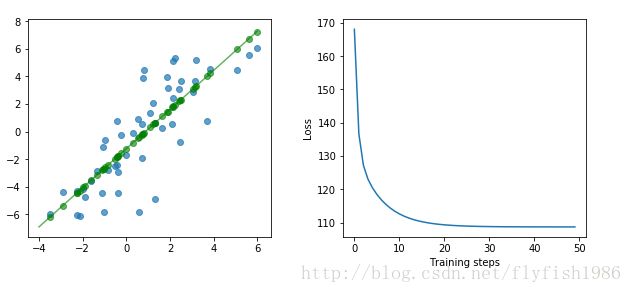
ax1.scatter(x, y, alpha=.7)
ax1.scatter(x, np.transpose(yhat)[0], c="g", alpha=.6)
line_x_range = (-4, 6)
ax1.plot(line_x_range, [betas[0] + a * betas[1] for a in line_x_range], "g", alpha=0.6)
ax2.plot(range(0, training_steps), losses)
ax2.set_ylabel("Loss")
ax2.set_xlabel("Training steps")
plt.show()

使用Eigen库 矩阵计算

#include <iostream>
#include "Dense"

int main()
{
    Eigen::MatrixXd x(4, 2);
    x(0, 0) = 1;
    x(1, 0) = 2;
    x(2, 0) = 3;
    x(3, 0) = 4;

    for (int i = 0; i < 4; ++i)
        x(i, 1) = 1;
    Eigen::MatrixXd xt = x.transpose();

    Eigen::MatrixXd y(4, 1);
    y(0, 0) = 6;
    y(1, 0) = 5;
    y(2, 0) = 7;
    y(3, 0) = 10;

    Eigen::MatrixXd result(2, 1);
    result = (xt * x).inverse() * xt * y;
    std::cout << "y = " << result(0, 0) << "x + " << result(1, 0) << "\n";

    system("pause");

    return 0;
}

重新再整理一下