Alpha-beta剪枝算法

Alpha-beta剪枝算法实例分析

转载  2015年05月11日 15:59:31

• 4128

看本章之前，请先参看前一篇文章《Minimax算法及实例分析》

由于Minimax算法有一个很大的问题就是计算复杂性。由于所需搜索的节点数随最大深度呈指数膨胀，而算法的效果往往和深度相关，因此这极大限制了算法的效果。

Alpha-beta剪枝是对Minimax的补充和改进。采用Alpha-beta剪枝后，我们可不必构造和搜索最大深度D内的所有节点，在构造过程中，如果发现当前格局再往下不能找到更好的解，我们就停止在这个格局及以下的搜索，也就是剪枝。

Alpha-beta基于这样一种朴素的思想：时时刻刻记得当前已经知道的最好选择，如果从当前格局搜索下去，不可能找到比已知最优解更好的解，则停止这个格局分支的搜索（剪枝），回溯到父节点继续搜索。

Alpha-beta算法可以看成变种的Minimax，基本方法是从根节点开始采用深度优先的方式构造格局树，在构造每个节点时，都会读取此节点的alpha和beta两个值，其中alpha表示搜索到当前节点时已知的最好选择的下界，而beta表示从这个节点往下搜索最坏结局的上界。由于我们假设对手会将局势引入最坏结局之一，因此当beta小于alpha时，表示从此处开始不论最终结局是哪一个，其上限价值也要低于已知的最优解，也就是说已经不可能此处向下找到更好的解，所以就会剪枝。

下面同样以上述示例介绍Alpha-beta剪枝算法的工作原理。我们从根节点开始，详述使用Alpha-beta的每一个步骤：

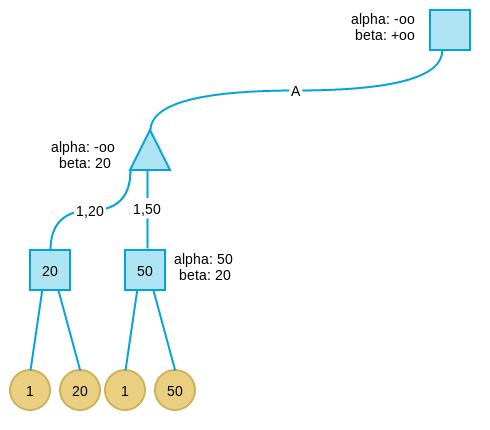
1. 根节点的alpha和beta分别被初始化为−∞，和+∞。
2. 深度优先搜索第一个孩子，不是叶子节点，所以alpha和beta继承自父节点，分别为−∞，和+∞
3. 搜索第三层的第一个孩子，同上。

4. 搜索第四层，到达叶子节点，采用评价函数得到此节点的评价值为1。

   

5. 此叶节点的父节点为max节点，因此更新其alpha值为1，表示此节点取值的下界为1。

6. 再看另外一个子节点，值为20，大于当前alpha值，因此将alpha值更新为20。
7. 此时第三层最左节点所有子树搜索完毕，作为max节点，更新其真实值为当前alpha值：20。

8. 由于其父节点（第二层最左节点）为min节点，因此更新其父节点beta值为20，表示这个节点取值最多为20。

   

9. 搜索第二层最左节点的第二个孩子及其子树，按上述逻辑，得到值为50（注意第二层最左节点的beta值要传递给孩子）。由于50大于20，不更新min节点的beta值。

   

10. 搜索第二层最左节点的第三个孩子。当看完第一个叶子节点后，发现第三个孩子的alpha=beta，此时表示这个节点下不会再有更好解，于是剪枝。

    

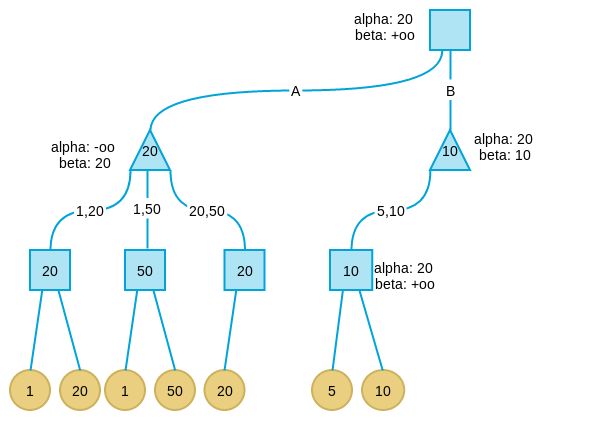
11. 继续搜索B分支，当搜索完B分支的第一个孩子后，发现此时B分支的alpha为20，beta为10。这表示B分支节点的最大取值不会超过10，而我们已经在A分支取到20，此时满足alpha大于等于beta的剪枝条件，因此将B剪枝。并将B分支的节点值设为10，注意，这个10不一定是这个节点的真实值，而只是上线，B节点的真实值可能是5，可能是1，可能是任何小于10的值。但是已经无所谓了，反正我们知道这个分支不会好过A分支，因此可以放弃了。

    

12. 在C分支搜索时遇到了与B分支相同的情况。因此讲C分支剪枝。

    

此时搜索全部完毕，而我们也得到了这一步的策略：应该走A分支。

可以看到相比普通Minimax要搜索18个叶子节点相比，这里只搜索了9个。采用Alpha-beta剪枝，可以在相同时间内加大Minimax的搜索深度，因此可以获得更好的效果。并且Alpha-beta的解和普通Minimax的解是一致的。