数据结构 - AVL树的Java实现
数据结构 - AVL树的Java实现
阅读本节前需要先阅读上一篇文章:https://blog.csdn.net/funnyrand/article/details/81665445,该文章讲述了二叉查询树的基本原理和Java实现。由于一般的二叉查询树不是自平衡的,所以当插入的数据已经排好序,或者对二叉查询树进行了大量的插入和删除操作,二叉查询树将会蜕变成链表,所有操作的算法复杂度会变为![]() 。因此,在实际项目中我们不会直接使用原始的二叉查询树,而是使用平衡二叉查询树,如红黑树,AVL树,伸展树,B-树等。本节将介绍AVL树的基本原理及Java实现。
。因此,在实际项目中我们不会直接使用原始的二叉查询树,而是使用平衡二叉查询树,如红黑树,AVL树,伸展树,B-树等。本节将介绍AVL树的基本原理及Java实现。
首先看看平衡性的判断。
一、判断二叉查询树是否平衡
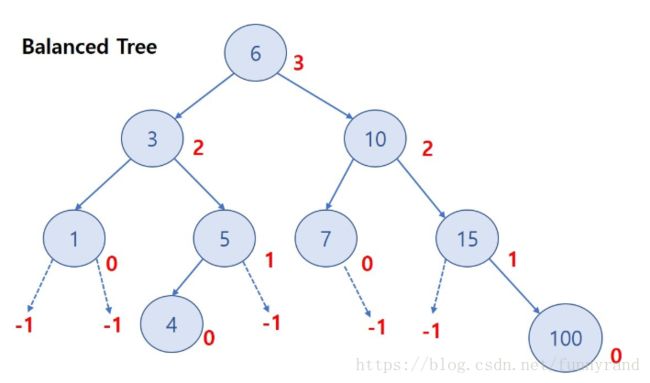
二叉查询树平衡的充分必要条件是其每个结点的左右子树高度差的绝对值小于等于1。叶子结点的高度为1,其父节点为2,依次增加,直到root结点。二叉查询树的高度就是root结点的高度。(注:以下图片引用自网络,虽然其定义叶子结点的高度为0,但不影响左右结点高度差的绝对值)
显然,下面的这棵二叉查询树是平衡的,
而以下这棵树是不平衡的,
因为结点4的左右结点高度差的绝对值为2,Math.abs(-1 - 1) = 2,所以其不平衡。
二、AVL树及其4种旋转
AVL树的名称来源于发明者的姓名(Adelson-Velsky and Landis)。AVL树是一种自平衡二叉查询树,每次进行完插入和删除操作后都会检查与插入结点和删除结点相关的结点的平衡性,一旦发现不平衡的结点,就采用某种旋转机制,使其达到平衡。所以,AVL树在任何状态下总是平衡的。理解AVL树的关键是掌握4种旋转机制,其它操作如遍历,查询等和原始的二叉查询树(BST)一样。
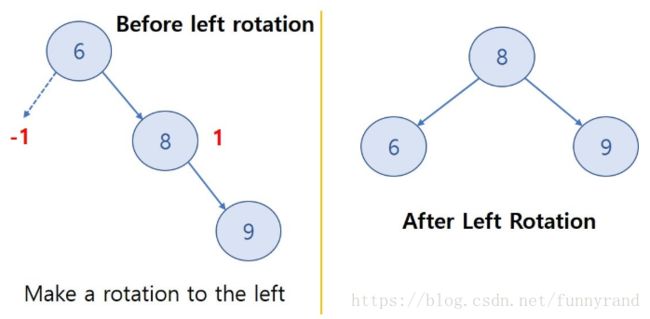
1. 左旋
如下图,将结点6左旋即可使其平衡。
2. 右旋
如下图,将结点6右旋即可使其平衡。
3. 左右旋
如下图,先将结点4左旋,再将结点6右旋即可使其平衡。
4. 右左旋
如下图,先将结点8右旋,再将结点6左旋即可使其平衡。
三、代码
由于AVL树继承自BinarySearchTree,所以下面的代码都是基于这篇文章中的代码:https://blog.csdn.net/funnyrand/article/details/81665445
定义AVLTreeNode和AVLTree,
package com.my.study.algorithm.tree.avltree;
import com.my.study.algorithm.tree.bstree.BinaryTreeNode;
/**
* AVL tree node.
*
* @param
* Element type
*/
public class AVLTreeNode> extends BinaryTreeNode {
// Balance number
private int balance;
public AVLTreeNode(E value) {
super(value);
}
public int getBalance() {
return balance;
}
public void setBalance(int balance) {
this.balance = balance;
}
}
package com.my.study.algorithm.tree.avltree;
import com.my.study.algorithm.tree.bstree.BinarySearchTree;
import com.my.study.algorithm.tree.bstree.IBinaryTreeNode;
/**
* This class demonstrates the usage of AVL tree.
*
* @param
* Element type.
*/
public class AVLTree> extends BinarySearchTree {
public AVLTree() {
super();
}
public AVLTree(E[] data) {
super(data);
}
@Override
public IBinaryTreeNode insert(E e) {
AVLTreeNode newNode = new AVLTreeNode(e);
// Empty tree, then create root node.
if (root == null) {
root = newNode;
} else {
insert(root, newNode);
}
reBalanceNode(newNode);
return newNode;
}
@Override
public IBinaryTreeNode remove(E e) {
IBinaryTreeNode node = find(root, e);
if (node == null) {
return null;
}
return remove(node);
}
/**
* Check if given node is balanced.
*
* @param node
* IBinaryTreeNode node
* @return true: balanced, false: not balanced
*/
public boolean isBalanced(IBinaryTreeNode node) {
int balance = getBalance(node);
return Math.abs(balance) <= 1;
}
/**
* Get balanced status of given node.
*
* @param node
* IBinaryTreeNode node
* @return <=-2: not balanced and left is heavy, -1,0,1: balanced, >=2 not
* balanced and right is heavy
*/
public int getBalance(IBinaryTreeNode node) {
if (node == null) {
return 0;
}
return ((AVLTreeNode) node).getBalance();
}
/**
* Re-balance of specified node.
*
* @param node
* IBinaryTreeNode
*/
protected void reBalance(IBinaryTreeNode node) {
if (node != null) {
int balance = getHeight(node.getRightNode()) - getHeight(node.getLeftNode());
((AVLTreeNode) node).setBalance(balance);
reBalance(node.getParentNode());
}
}
/*
* Remove an element and keep balance.
*
* @param node node to remove
*
* @return the parent node of removed node
*/
private IBinaryTreeNode remove(IBinaryTreeNode node) {
// Leaf node, just remove it
if (node.getLeftNode() == null && node.getRightNode() == null) {
IBinaryTreeNode parentNode = null;
if (node.getParentNode() == null) {
root = null;
} else {
parentNode = node.getParentNode();
if (node.isLeft()) {
parentNode.setLeftNode(null);
} else {
parentNode.setRightNode(null);
}
// Re-balance node after removing
reBalanceNode(parentNode);
}
return parentNode;
}
// If current node has left node ,then find its previous node, exchange value
// and then remove previous node.
if (node.getLeftNode() != null) {
IBinaryTreeNode preNode = findPre(node);
node.setValue(preNode.getValue());
return remove(preNode);
} else {
// If current node has right node, then find its next node, exchange value and
// then remove next node.
IBinaryTreeNode nextNode = findNext(node);
node.setValue(nextNode.getValue());
return remove(nextNode);
}
}
/*
* Reset balance and height.
*/
private void resetBalanceAndHeight(IBinaryTreeNode node) {
reHeight(node);
reBalance(node);
}
/*
* Re-balance tree node.
*
* @param node IBinaryTreeNode node
*/
private void reBalanceNode(IBinaryTreeNode node) {
if (node == null) {
return;
}
resetBalanceAndHeight(node);
// Only need to re-balance when balance <= -2 or balance >= 2
int balance = getBalance(node);
// Left heavy
if (balance <= -2) {
// Right
if (getHeight(node.getLeftNode().getLeftNode()) >= getHeight(node.getLeftNode().getRightNode())) {
node = rotateRight(node);
} else {
// Left->Right
node = rotateLeftThenRight(node);
}
// Right heavy
} else if (balance >= 2) {
// Left
if (getHeight(node.getRightNode().getRightNode()) >= getHeight(node.getRightNode().getLeftNode())) {
node = rotateLeft(node);
} else {
// Right->Left
node = rotateRightThenLeft(node);
}
}
// Re-balance node's parent node due to the propagation of unbalanced node
if (node.getParentNode() != null) {
reBalanceNode(node.getParentNode());
} else {
// After rotate, root node may be changed
root = node;
}
}
/*
* Left rotation.
*/
private IBinaryTreeNode rotateLeft(IBinaryTreeNode nodeA) {
IBinaryTreeNode nodeB = nodeA.getRightNode();
nodeB.setParentNode(nodeA.getParentNode());
nodeA.setRightNode(nodeB.getLeftNode());
if (nodeB.getParentNode() != null) {
if (nodeA.isLeft()) {
nodeB.getParentNode().setLeftNode(nodeB);
} else {
nodeB.getParentNode().setRightNode(nodeB);
}
}
nodeB.setLeftNode(nodeA);
resetBalanceAndHeight(nodeA);
resetBalanceAndHeight(nodeB);
return nodeB;
}
/*
* Right rotation.
*/
private IBinaryTreeNode rotateRight(IBinaryTreeNode nodeA) {
IBinaryTreeNode nodeB = nodeA.getLeftNode();
nodeB.setParentNode(nodeA.getParentNode());
nodeA.setLeftNode(nodeB.getRightNode());
if (nodeB.getParentNode() != null) {
if (nodeA.isLeft()) {
nodeB.getParentNode().setLeftNode(nodeB);
} else {
nodeB.getParentNode().setRightNode(nodeB);
}
}
nodeB.setRightNode(nodeA);
resetBalanceAndHeight(nodeA);
resetBalanceAndHeight(nodeB);
return nodeB;
}
/*
* Left rotation then right rotation.
*/
private IBinaryTreeNode rotateLeftThenRight(IBinaryTreeNode node) {
node.setLeftNode(rotateLeft(node.getLeftNode()));
return rotateRight(node);
}
/*
* Right rotation then left rotation.
*/
private IBinaryTreeNode rotateRightThenLeft(IBinaryTreeNode node) {
node.setRightNode(rotateRight(node.getRightNode()));
return rotateLeft(node);
}
}
测试类AVLTreeTest,
package com.my.study.algorithm.tree.avltree;
import java.util.Arrays;
import java.util.Date;
import java.util.List;
import com.my.study.algorithm.tree.bstree.BinarySearchTree;
import com.my.study.algorithm.tree.bstree.BinaryTreePrinter;
import com.my.study.algorithm.tree.bstree.IBinaryTree;
public class AVLTreeTest> extends BinarySearchTree {
public static void main(String[] args) {
generateAVLTreeByOrderedArray();
// generateAVLTreeByOrderedArrayInserting();
// testRemoveElement();
// testPerformance();
}
public static void generateAVLTreeByOrderedArray() {
Integer[] array = { 0, 0, 1, 1, 1, 1, 2, 3, 4, 5, 6, 7, 8 };
IBinaryTree tree = new AVLTree<>(array);
printTreeInfo(tree);
}
public static void generateAVLTreeByOrderedArrayInserting() {
IBinaryTree tree = new AVLTree<>();
Integer[] array2 = { 8, 8, 8, 7, 6, 5, 4, 3, 2, 1, 0, 0 };
tree = new AVLTree<>();
for (int data : array2) {
tree.insert(data);
System.out.println("Inserted: " + data);
printTreeInfo(tree);
}
}
public static void testRemoveElement() {
Integer[] array = { 0, 0, 1, 1, 1, 1, 2, 3, 4, 5, 6, 7, 8 };
IBinaryTree tree = new AVLTree<>(array);
printTreeInfo(tree);
for (int data : array) {
tree.remove(data);
System.out.println("Removed: " + data);
printTreeInfo(tree);
}
}
public static void testPerformance() {
// Original data size
int originalDataSize = 1000000;
int minNum = 0;
int maxNum = originalDataSize;
Integer[] data = generateRandomArrays(minNum, maxNum, originalDataSize);
// Generate tree
long time1 = new Date().getTime();
IBinaryTree tree = new AVLTree<>(data);
long time2 = new Date().getTime();
System.out.println("Generate tree takes: " + (time2 - time1) / 1000 + " seconds, tree size: " + tree.getSize());
System.out.println("Is root balanced: " + ((AVLTree) tree).isBalanced(tree.getRoot()));
// Get some node after trave
List datas = tree.inorderTraversal();
System.out.println("Last 100 data:");
System.out.println(Arrays.toString(datas.subList(originalDataSize - 100, datas.size()).toArray()));
}
private static Integer[] generateRandomArrays(int min, int max, int size) {
Integer[] data = new Integer[size];
for (int i = 0; i < size; i++) {
int num = (int) (Math.random() * (max - min + 1)) + min;
data[i] = num;
}
return data;
}
private static > void printTreeInfo(IBinaryTree tree) {
System.out.println("Tree height: " + (tree.getRoot() == null ? 0 : tree.getRoot().getHeight()));
System.out.println("Tree size: " + tree.getSize());
System.out.println("Pre order traversal: " + tree.preorderTraversal());
System.out.println("In order traversal: " + tree.inorderTraversal());
System.out.println("Post order traversal: " + tree.postorderTraversal());
System.out.println("Tree structure:");
BinaryTreePrinter.printTree(tree);
System.out.println("-----------------------------------------------");
}
}
四、AVL树的测试
1. generateAVLTreeByOrderedArray
该方法测试用一个已经排好序的数组来生成AVL树,检查生成的AVL树是否平衡。
输出结果:
Tree height: 4
Tree size: 13
Pre order traversal: [3, 1, 0, 0, 1, 1, 1, 2, 5, 4, 7, 6, 8]
In order traversal: [0, 0, 1, 1, 1, 1, 2, 3, 4, 5, 6, 7, 8]
Post order traversal: [0, 1, 0, 1, 2, 1, 1, 4, 6, 8, 7, 5, 3]
Tree structure:
3
/ \
/ \
/ \
/ \
1 5
/ \ / \
/ \ / \
0 1 4 7
/ \ / \ / \
0 1 1 2 6 8
-----------------------------------------------
2. generateAVLTreeByOrderedArrayInserting
该方法演示了在插入数据后如何通过旋转保持平衡。
输出结果:
Inserted: 8
Tree height: 1
Tree size: 1
Pre order traversal: [8]
In order traversal: [8]
Post order traversal: [8]
Tree structure:
8
-----------------------------------------------
Inserted: 8
Tree height: 2
Tree size: 2
Pre order traversal: [8, 8]
In order traversal: [8, 8]
Post order traversal: [8, 8]
Tree structure:
8
/
8
-----------------------------------------------
Inserted: 8
Tree height: 2
Tree size: 3
Pre order traversal: [8, 8, 8]
In order traversal: [8, 8, 8]
Post order traversal: [8, 8, 8]
Tree structure:
8
/ \
8 8
-----------------------------------------------
Inserted: 7
Tree height: 3
Tree size: 4
Pre order traversal: [8, 8, 7, 8]
In order traversal: [7, 8, 8, 8]
Post order traversal: [7, 8, 8, 8]
Tree structure:
8
/ \
/ \
8 8
/
7
-----------------------------------------------
Inserted: 6
Tree height: 3
Tree size: 5
Pre order traversal: [8, 7, 6, 8, 8]
In order traversal: [6, 7, 8, 8, 8]
Post order traversal: [6, 8, 7, 8, 8]
Tree structure:
8
/ \
/ \
7 8
/ \
6 8
-----------------------------------------------
Inserted: 5
Tree height: 3
Tree size: 6
Pre order traversal: [7, 6, 5, 8, 8, 8]
In order traversal: [5, 6, 7, 8, 8, 8]
Post order traversal: [5, 6, 8, 8, 8, 7]
Tree structure:
7
/ \
/ \
6 8
/ / \
5 8 8
-----------------------------------------------
Inserted: 4
Tree height: 3
Tree size: 7
Pre order traversal: [7, 5, 4, 6, 8, 8, 8]
In order traversal: [4, 5, 6, 7, 8, 8, 8]
Post order traversal: [4, 6, 5, 8, 8, 8, 7]
Tree structure:
7
/ \
/ \
5 8
/ \ / \
4 6 8 8
-----------------------------------------------
Inserted: 3
Tree height: 4
Tree size: 8
Pre order traversal: [7, 5, 4, 3, 6, 8, 8, 8]
In order traversal: [3, 4, 5, 6, 7, 8, 8, 8]
Post order traversal: [3, 4, 6, 5, 8, 8, 8, 7]
Tree structure:
7
/ \
/ \
/ \
/ \
5 8
/ \ / \
/ \ / \
4 6 8 8
/
3
-----------------------------------------------
Inserted: 2
Tree height: 4
Tree size: 9
Pre order traversal: [7, 5, 3, 2, 4, 6, 8, 8, 8]
In order traversal: [2, 3, 4, 5, 6, 7, 8, 8, 8]
Post order traversal: [2, 4, 3, 6, 5, 8, 8, 8, 7]
Tree structure:
7
/ \
/ \
/ \
/ \
5 8
/ \ / \
/ \ / \
3 6 8 8
/ \
2 4
-----------------------------------------------
Inserted: 1
Tree height: 4
Tree size: 10
Pre order traversal: [7, 3, 2, 1, 5, 4, 6, 8, 8, 8]
In order traversal: [1, 2, 3, 4, 5, 6, 7, 8, 8, 8]
Post order traversal: [1, 2, 4, 6, 5, 3, 8, 8, 8, 7]
Tree structure:
7
/ \
/ \
/ \
/ \
3 8
/ \ / \
/ \ / \
2 5 8 8
/ / \
1 4 6
-----------------------------------------------
Inserted: 0
Tree height: 4
Tree size: 11
Pre order traversal: [7, 3, 1, 0, 2, 5, 4, 6, 8, 8, 8]
In order traversal: [0, 1, 2, 3, 4, 5, 6, 7, 8, 8, 8]
Post order traversal: [0, 2, 1, 4, 6, 5, 3, 8, 8, 8, 7]
Tree structure:
7
/ \
/ \
/ \
/ \
3 8
/ \ / \
/ \ / \
1 5 8 8
/ \ / \
0 2 4 6
-----------------------------------------------
Inserted: 0
Tree height: 4
Tree size: 12
Pre order traversal: [3, 1, 0, 0, 2, 7, 5, 4, 6, 8, 8, 8]
In order traversal: [0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 8, 8]
Post order traversal: [0, 0, 2, 1, 4, 6, 5, 8, 8, 8, 7, 3]
Tree structure:
3
/ \
/ \
/ \
/ \
1 7
/ \ / \
/ \ / \
0 2 5 8
/ / \ / \
0 4 6 8 8
-----------------------------------------------
3. testRemoveElement
该方法演示了在删除结点后AVL树如何通过旋转保持平衡。
输出结果:
Tree height: 4
Tree size: 13
Pre order traversal: [3, 1, 0, 0, 1, 1, 1, 2, 5, 4, 7, 6, 8]
In order traversal: [0, 0, 1, 1, 1, 1, 2, 3, 4, 5, 6, 7, 8]
Post order traversal: [0, 1, 0, 1, 2, 1, 1, 4, 6, 8, 7, 5, 3]
Tree structure:
3
/ \
/ \
/ \
/ \
1 5
/ \ / \
/ \ / \
0 1 4 7
/ \ / \ / \
0 1 1 2 6 8
-----------------------------------------------
Removed: 0
Tree height: 4
Tree size: 12
Pre order traversal: [3, 1, 0, 1, 1, 1, 2, 5, 4, 7, 6, 8]
In order traversal: [0, 1, 1, 1, 1, 2, 3, 4, 5, 6, 7, 8]
Post order traversal: [1, 0, 1, 2, 1, 1, 4, 6, 8, 7, 5, 3]
Tree structure:
3
/ \
/ \
/ \
/ \
1 5
/ \ / \
/ \ / \
0 1 4 7
\ / \ / \
1 1 2 6 8
-----------------------------------------------
Removed: 0
Tree height: 4
Tree size: 11
Pre order traversal: [3, 1, 1, 1, 1, 2, 5, 4, 7, 6, 8]
In order traversal: [1, 1, 1, 1, 2, 3, 4, 5, 6, 7, 8]
Post order traversal: [1, 1, 2, 1, 1, 4, 6, 8, 7, 5, 3]
Tree structure:
3
/ \
/ \
/ \
/ \
1 5
/ \ / \
/ \ / \
1 1 4 7
/ \ / \
1 2 6 8
-----------------------------------------------
Removed: 1
Tree height: 4
Tree size: 10
Pre order traversal: [3, 1, 1, 1, 2, 5, 4, 7, 6, 8]
In order traversal: [1, 1, 1, 2, 3, 4, 5, 6, 7, 8]
Post order traversal: [1, 1, 2, 1, 4, 6, 8, 7, 5, 3]
Tree structure:
3
/ \
/ \
/ \
/ \
1 5
/ \ / \
/ \ / \
1 2 4 7
\ / \
1 6 8
-----------------------------------------------
Removed: 1
Tree height: 4
Tree size: 9
Pre order traversal: [3, 1, 1, 2, 5, 4, 7, 6, 8]
In order traversal: [1, 1, 2, 3, 4, 5, 6, 7, 8]
Post order traversal: [1, 2, 1, 4, 6, 8, 7, 5, 3]
Tree structure:
3
/ \
/ \
/ \
/ \
1 5
/ \ / \
/ \ / \
1 2 4 7
/ \
6 8
-----------------------------------------------
Removed: 1
Tree height: 4
Tree size: 8
Pre order traversal: [3, 1, 2, 5, 4, 7, 6, 8]
In order traversal: [1, 2, 3, 4, 5, 6, 7, 8]
Post order traversal: [2, 1, 4, 6, 8, 7, 5, 3]
Tree structure:
3
/ \
/ \
/ \
/ \
1 5
\ / \
\ / \
2 4 7
/ \
6 8
-----------------------------------------------
Removed: 1
Tree height: 3
Tree size: 7
Pre order traversal: [5, 3, 2, 4, 7, 6, 8]
In order traversal: [2, 3, 4, 5, 6, 7, 8]
Post order traversal: [2, 4, 3, 6, 8, 7, 5]
Tree structure:
5
/ \
/ \
3 7
/ \ / \
2 4 6 8
-----------------------------------------------
Removed: 2
Tree height: 3
Tree size: 6
Pre order traversal: [5, 3, 4, 7, 6, 8]
In order traversal: [3, 4, 5, 6, 7, 8]
Post order traversal: [4, 3, 6, 8, 7, 5]
Tree structure:
5
/ \
/ \
3 7
\ / \
4 6 8
-----------------------------------------------
Removed: 3
Tree height: 3
Tree size: 5
Pre order traversal: [5, 4, 7, 6, 8]
In order traversal: [4, 5, 6, 7, 8]
Post order traversal: [4, 6, 8, 7, 5]
Tree structure:
5
/ \
/ \
4 7
/ \
6 8
-----------------------------------------------
Removed: 4
Tree height: 3
Tree size: 4
Pre order traversal: [7, 5, 6, 8]
In order traversal: [5, 6, 7, 8]
Post order traversal: [6, 5, 8, 7]
Tree structure:
7
/ \
/ \
5 8
\
6
-----------------------------------------------
Removed: 5
Tree height: 2
Tree size: 3
Pre order traversal: [7, 6, 8]
In order traversal: [6, 7, 8]
Post order traversal: [6, 8, 7]
Tree structure:
7
/ \
6 8
-----------------------------------------------
Removed: 6
Tree height: 2
Tree size: 2
Pre order traversal: [7, 8]
In order traversal: [7, 8]
Post order traversal: [8, 7]
Tree structure:
7
\
8
-----------------------------------------------
Removed: 7
Tree height: 1
Tree size: 1
Pre order traversal: [8]
In order traversal: [8]
Post order traversal: [8]
Tree structure:
8
-----------------------------------------------
Removed: 8
Tree height: 0
Tree size: 0
Pre order traversal: []
In order traversal: []
Post order traversal: []
Tree structure:
-----------------------------------------------
4. testPerformance
性能测试,检查插入1000000条随机数据的速度以及中序遍历后的后100个元素值。
输出结果:
Generate tree takes: 3 seconds, tree size: 1000000
Is root balanced: true
Last 100 data:
[999892, 999892, 999893, 999895, 999895, 999899, 999899, 999902, 999903, 999903, 999905, 999905, 999906, 999907, 999909, 999909, 999909, 999911, 999911, 999911, 999912, 999912, 999913, 999914, 999916, 999917, 999917, 999918, 999919, 999919, 999919, 999922, 999923, 999926, 999928, 999928, 999928, 999928, 999930, 999931, 999932, 999934, 999936, 999936, 999937, 999939, 999942, 999942, 999950, 999950, 999950, 999954, 999955, 999956, 999958, 999958, 999958, 999959, 999959, 999960, 999962, 999962, 999964, 999964, 999964, 999965, 999966, 999967, 999969, 999969, 999970, 999970, 999972, 999972, 999972, 999973, 999973, 999975, 999975, 999977, 999978, 999978, 999978, 999979, 999981, 999981, 999982, 999983, 999984, 999987, 999987, 999988, 999990, 999991, 999991, 999994, 999995, 999996, 999997, 999998]
五、AVL树操作的算法复杂度
算法复杂度与二叉查询树一样,
| 操作 | 平均复杂度 | 最坏复杂度 |
|---|---|---|
| 空间 | ||
| 查询 | ||
| 插入 | ||
| 删除 |