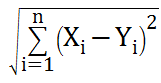【机器学习】欧几里德距离和皮尔逊相关系数（笔记）

欧几里德距离（）

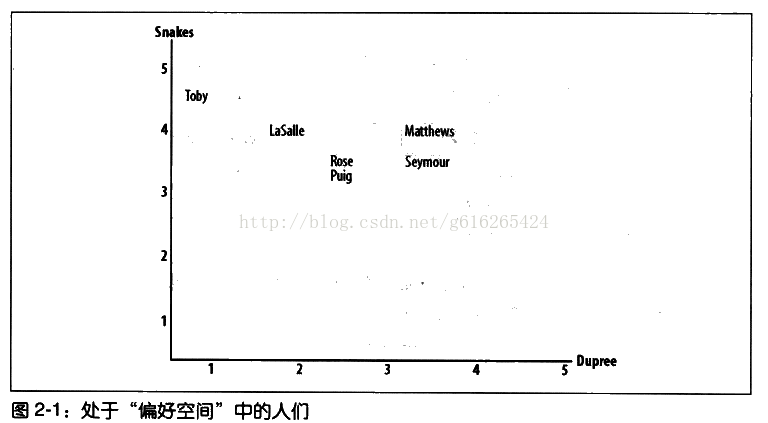
欧几里德距离和皮尔逊相关系数在机器学习中都是对相关度的计算，欧几里德距离是以人们一直评价的物品作为坐标轴，将参与评价的人绘制到图中，并考察他们彼此距离的远近。例子（摘自集体智慧编程）：

#数据集
critics={
    'Lisa Rose': {
        'Lady in the Water': 2.5,
        'Snakes on a Plane': 3.5,
        'Just My Luck': 3.0,
        'Superman Returns': 3.5,
        'You, Me and Dupree': 2.5,
        'The Night Listener': 3.0
    },
    'Gene Seymour': {
        'Lady in the Water': 3.0,
        'Snakes on a Plane': 3.5,
        'Just My Luck': 1.5,
        'Superman Returns': 5.0,
        'The Night Listener': 3.0,
        'You, Me and Dupree': 3.5
    },
    'Michael Phillips': {
        'Lady in the Water': 2.5,
        'Snakes on a Plane': 3.0,
        'Superman Returns': 3.5,
        'The Night Listener': 4.0
    },
    'Claudia Puig': {
        'Snakes on a Plane': 3.5,
        'Just My Luck': 3.0,
        'The Night Listener': 4.5,
        'Superman Returns': 4.0,
        'You, Me and Dupree': 2.5
    },
    'Mick LaSalle': {
        'Lady in the Water': 3.0,
        'Snakes on a Plane': 4.0,
        'Just My Luck': 2.0,
        'Superman Returns': 3.0,
        'The Night Listener': 3.0,
        'You, Me and Dupree': 2.0
    },
    'Jack Matthews': {
        'Lady in the Water': 3.0,
        'Snakes on a Plane': 4.0,
        'The Night Listener': 3.0,
        'Superman Returns': 5.0,
        'You, Me and Dupree': 3.5
    },
    'Toby': {
        'Snakes on a Plane': 4.5,
        'You, Me and Dupree': 1.0,
        'Superman Returns': 4.0
    }
}

当我想知道任意两个人的相似度（根据电影评分）：

from math import sqrt
#欧几里得距离
def sim_distance_ou(prefs,person1,person2):
    #创建一个空集合用来存储用户1和用户2都有的电影的评分
    si={}
    #使用用户1里评分的电影名去遍历检索用户2的评分的电影名，如果同时存在，往si集合中加上这个电影名并且赋值为1
    for item in prefs[person1]:
        if item in prefs[person2]:
            si[item]=1

    #如果两个用户没有同时存在的电影的评分，则跳出循环
    #si数据结构：{'Superman Returns': 1, 'Snakes on a Plane': 1}
    if len(si)==0:return 0
    #计算所有差值的平方和
    sum_of_squares = sum([pow(prefs[person1][item]-prefs[person2][item],2)
                         for item in si])
    #对加和的结果进行开根，加1是为了避免被0整除
    return 1/(1+sqrt(sum_of_squares))

#比如我求Michael Phillips和Toby的相似度
#得到结果
0.38742588672279304

皮尔逊相关系数（）

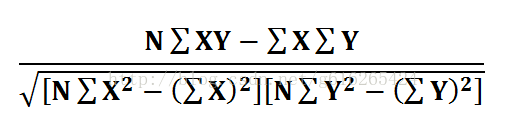皮尔逊相关系数其实是在欧几里德距离上做了一部分优化，对向量的值首先做了中心化（对两个向量中的所有维度都减去元素的平均值），之后在对中心化的结果求余弦相似度（而余弦计算要求每个向量中所有的值都必须非空，如果我有两个向量v1(3,2,4)、v2(-1,2,null)，这两个向量是无法进行余弦计算的，因为向量v2中有null值）（余弦相似度是两个向量在空间中夹角的大小，值域为[-1,1]，1代表0°，完全重叠；-1代表180°，完全相反）
，结果介于[-1,1]之间，其实就是协方差，两个向量，当一个向量随着另一个向量的增大而增大时，结果就是正值，反之则是负值，当结果为0时，两个向量间不存在线性关系。

总结：皮尔逊相关系数的思路就是把向量中所有null维度赋值为0，对向量做中心化，中心化后所有维度的平均值基本为0，再对结果进行余弦计算。

#皮尔逊相关系数
def sim_distance_pi(prefs,person1,person2):
    si={}
    for item in prefs[person1]:
        if item in prefs[person2]:
            si[item]=1

    n=len(si)
    if n==0:return 1

    #对所有偏好求和
    sum1=sum([prefs[person1][item] for item in si])
    sum2=sum([prefs[person2][item] for item in si])

    #求平方和
    sum1Sq=sum([pow(prefs[person1][item],2) for item in si])
    sum2Sq=sum([pow(prefs[person2][item],2) for item in si])

    #求乘积和
    pSum=sum([prefs[person1][item]*prefs[person2][item] for item in si])

    #计算皮尔逊相关系数
    num=pSum-(sum1*sum2/n)
    den=sqrt((sum1Sq-pow(sum1,2)/n)*(sum2Sq-pow(sum2,2)/n))
    if den==0:return 0

    result=num/den

    return result

总结：

1、皮尔逊相关系数是对欧几里德距离的优化

2、欧几里德距离是基于物品求用户相似度（不知道能不能做基于用户求物品相似度，欢迎纠正错误）

3、代码对照着公式来写，很好写