深度置信网络（二）：玻尔兹曼机

HopField网络中，我们引入了网络能量的定义：

E=−∑isibi−∑i<jsisjwij E = − ∑ i s i b i − ∑ i < j s i s j w i j

网络中神经元的状态的更新总是朝着使网络能量降低的方向变化：

Energy gap=ΔEi=E(si=0)−E(sj=1)=bi+∑jsjwij E n e r g y   g a p = Δ E i = E ( s i = 0 ) − E ( s j = 1 ) = b i + ∑ j s j w i j

si={01ΔEi<=0ΔEi>0(1) (1) s i = { 0 Δ E i <= 0 1 Δ E i > 0

其实这事一个贪心的思路，每一步都朝着能量降低的方向变化，希望达到全局的能量最低，但是希望不总是会实现的。这种贪心的思路不能重视得到全局最优解。也就是说，HopField网络吸引子的能量不一定是全局最低的。

那么有没有办法达到全局能量的最低值呢？

有，来看一下模拟退火算法

模拟退火算法

现在，让我们的神经元按照一定的概率来更新状态：

p(si=1)=11+e−ΔEi/T p ( s i = 1 ) = 1 1 + e − Δ E i / T

si={01p(si=1)<=0.5p(si=1)>0.5(2) (2) s i = { 0 p ( s i = 1 ) <= 0.5 1 p ( s i = 1 ) > 0.5

可以看出，i神经元取状态1的概率不仅与自己的 Energy gap E n e r g y   g a p 有关，还跟参数T有关。

• 当 ΔEi=0 Δ E i = 0 ， p(si=1)=0.5 p ( s i = 1 ) = 0.5 ，也就是有一半概率取1，一半概率取0.
• 当 ΔEi>0 Δ E i > 0 ， p(si=1)>0.5 p ( s i = 1 ) > 0.5 ，也就是说取状态值1的概率较大；这时候如果T的值越大，则 p(si=1)→0.5 p ( s i = 1 ) → 0.5 ，T的值越小，则 p(si=1)→1 p ( s i = 1 ) → 1 .
• 当 ΔEi<0 Δ E i < 0 ， p(si=1)<0.5 p ( s i = 1 ) < 0.5 ，也就是说取状态值0的概率较大；这时候如果T的值较大，则 p(si=1)→0.5 p ( s i = 1 ) → 0.5 ,T的值越小，则 p(si=1)→0 p ( s i = 1 ) → 0

可以看出，在 ΔEi Δ E i 固定的情况下，T越大，则状态变化趋向随机变化（概念为0.5），能量往降低和升高的方向变化的概率接近一致；T越小，则 ΔEi Δ E i 的作用越大，状态变化趋向于能量降低的概率越大。这的参数T可以理解为温度。

在温度T固定的情况下，网络经过一定次数的状态迁移，也会收敛到一个稳定的状态。但是跟HopField的网络的稳定状态是有差别的，这里的稳定状态不是说网络固定到一个的状态不再改变，而是在这个状态下，任何一个组态出现的概率不在变化，而网络的实际状态还是一直处于变化中的。也就是说网络组态的概率分布稳定了。

这个状态称之为热平衡状态。

热平衡状态可能不太好理解，这里举个例子说明一下：比如我们的网络有三个神经元，所以网络可能的组态有 000,001,010,011,100,101,110,111 000 , 001 , 010 , 011 , 100 , 101 , 110 , 111 八种。热平衡状态下，网络可能不会固定在其中任何一种组态下而不再变化，而是在其中的一些组态之间来回变化，但是每个组态出现的概率是一定的，这时候就说明网络达到了热平衡状态。

在实际过程中，我们的温度T初始值一般比较高，然后不断的降低温度T，这样不断的让网络达到一个热平衡状态，就有很大的概率找到全局的温度最低点。相比我们之前HopField网络，我们的状态决策过程有可能跳出局部的问题最低点，因为我们的决策过程是按概率执行的，这就是模拟退火算法相比之前的算法的优点。

玻尔兹曼机

上一章结束的时候，提到HopField网络可以用来除了可以用来记忆数据外，还可以用于”解释”数据：将模型神经元分为可视部分和隐藏部分，可视部分用于数据的输入，隐藏部分用于输入数据的解释。解释的好坏取决于网络的能量值。

其实，将这个划分了可视部分和隐藏部分的模型中的神经元替换为上面提到的随机变化的神经元，就得到了一个随机神经网络，也就是玻尔兹曼机。

上一节我们介绍的模拟退火算法解决了寻找玻尔兹曼机全局能量最低点的问题，接下来，我们讨论第二个问题，怎么训练玻尔兹曼机的参数。

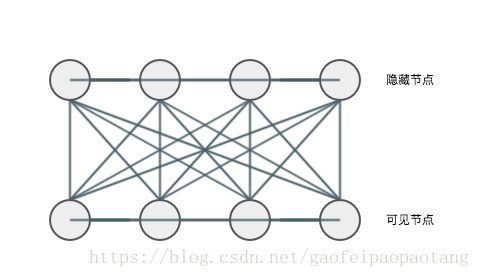
首先我们来看一下玻尔兹曼机的结构：

图1：玻尔兹曼机

玻尔兹曼机的网络能量定义：

E(v,h)=−∑ivibi−∑khkbk−∑i<jvivjwij−∑i,kvihkwik−∑k<lhkhlwkl E ( v , h ) = − ∑ i v i b i − ∑ k h k b k − ∑ i < j v i v j w i j − ∑ i , k v i h k w i k − ∑ k < l h k h l w k l

其中v表示所有的可视神经元，h表示所有的隐藏神经元。

玻尔兹曼机在达到热平衡状态后，其中神经元的状态分布符合玻尔兹曼分布，也就是：

P(v,h)=e−E(v,h)∑u,ge−E(u,g) P ( v , h ) = e − E ( v , h ) ∑ u , g e − E ( u , g )

那么，玻尔兹曼机是如何”解释”输入数据的呢？

我们可以训练玻尔兹曼机，使得可视神经元中出现输入数据的概率最大化（因为没法像HopField网络那样让神经元固定在输入数据上），此时的隐藏层的状态就可以视为输入数据的一个”解释”.

总之我们的玻尔兹曼机的训练目标是最大化概率：

P(v)=∑he−E(v,h)∑u,ge−E(u,g) P ( v ) = ∑ h e − E ( v , h ) ∑ u , g e − E ( u , g )

玻尔兹曼机的训练目标对于初学者来说，可能有些晦涩难懂，网络上的不同资料中采用的表述方式也有差异，比如：

• 使玻尔兹曼机赋予训练数据的概率最大化
• 使玻尔兹曼机中重现训练数据的概率最大化

这里我举个例子来说明一下：比如我们准备了输入数据000,001,并为它构建了一个包含3个可视神经元和n个隐藏
神经元的玻尔兹曼机，经过模拟退火算法这个模型会达到热平衡状态。这时候我们对可视节点进行采样。我们可能
会采集到我们的输入数据，也可能采集不到。采集到输入数据的概率由模型的参数决定的。那么我们的训练目标就
是学习到这样一些参数，使我们上面的的采样过程采集到输入数据的概率最大。

玻尔兹曼机的训练

为了训练玻尔兹曼机，最大化 P(v) P ( v ) ，首先想到的就是梯度下降法，经过公式的推导和简化得出下面这个惊人简单的公式：

∂logp(v)∂wij=⟨sisj⟩v−⟨sisj⟩model ∂ l o g p ( v ) ∂ w i j = ⟨ s i s j ⟩ v − ⟨ s i s j ⟩ m o d e l

Δwij=⟨sisj⟩data−⟨sisj⟩model Δ w i j = ⟨ s i s j ⟩ d a t a − ⟨ s i s j ⟩ m o d e l

以上公式中， ⟨⟩ ⟨ ⟩ 表示期望值。

玻尔兹曼机的参数训练过程分为正向和反向两个阶段:

• 设置初始权值 wij w i j
• 进入正向学习阶段，输入数据并钳制可视神经元的状态，不参与状态变化
• 进入模拟退火算法，直至网络达到热平衡
• 统计该热平衡状态下任意两个神经元同时为1的概率 pij p i j
• 进入反向学习阶段，输入数据并且可视神经元参与状态变化
• 进入模拟退火算法，直至网络达到热平衡
• 统计该状态下任意两个神经元同时为1的概率 pij p i j
• 更新权值 wij=wij+Δwij=wij+η(pij−p′ij) w i j = w i j + Δ w i j = w i j + η ( p i j − p i j ′ )
• 重复以上过程直至 wij w i j 不再变化或则变化足够小为止