mxnet 学习率设置详解

学习率

目前深度学习使用的都是非常简单的一阶收敛算法，梯度下降法，不管有多少自适应的优化算法，本质上都是对梯度下降法的各种变形，所以初始学习率对深层网络的收敛起着决定性的作用，下面就是梯度下降法的公式
$$\omega :=\omega -\alpha \ast \frac{\alpha }{\alpha \omega }loss(\omega )$$

\alpha 就是学习率，如果学习率太小，会导致网络loss下降非常慢，如果学习率太大，那么参数更新的幅度就非常大，就会导致网络收敛到局部最优点，或者loss直接开始增加，如下图所示。

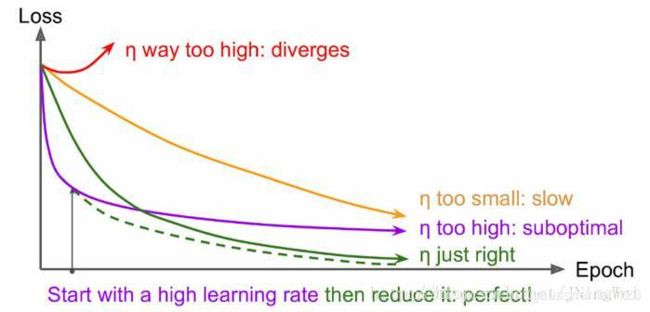
学习率的选择策略在网络的训练过程中是不断在变化的，在刚开始的时候，参数比较随机，所以我们应该选择相对较大的学习率，这样loss下降更快；当训练一段时间之后，参数的更新就应该有更小的幅度，所以学习率一般会做衰减，衰减的方式也非常多，比如到一定的步数将学习率乘上0.1，也有指数衰减等。

mxnet 学习率设置方法

学习率是优化器类optimizer的一个参数，设置学习率，就是给优化器传递这个参数，通常有两大类，一是静态常数学习率，可以在构造optimizer的时候传入常数参数即可；还有一种是动态设置学习率，mxnet提供ls_scheduler模块来完成动态设置。

静态常数

sgd_optimizer = mx.optimizer.SGD(learning_rate=0.03, lr_scheduler=schedule)
trainer = mx.gluon.Trainer(params=net.collect_params(), optimizer=sgd_optimizer)

动态设置

构造一个ls_scheduler,作为变量传递给优化器，当做优化器的ls_scheduler参数。

lrs #学习率调整策略
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
'learning_rate': learning_rate, 'wd': 0.001, 'lr_scheduler' : lrs})

基类LRScheduler

class mxnet.lr_scheduler.LRScheduler(base_lr=0.01, warmup_steps=0, warmup_begin_lr=0, warmup_mode='linear')

• base_lr 基础学习率
• warmup_steps 需要多少次steps来增长到base_lr
• warmup_begin_lr 初始学习率值
• warmup_mode 有’linear’ 和 'constant’两种模式，linear会持续增长学习率(以固定值)，constant会保持warmup_begin_lr不变

	def get_warmup_lr(self, num_update):
        assert num_update < self.warmup_steps
        if self.warmup_mode == 'linear':
            increase = (self.warmup_final_lr - self.warmup_begin_lr) \
                       * float(num_update) / float(self.warmup_steps)
            return self.warmup_begin_lr + increase
        elif self.warmup_mode == 'constant':
            return self.warmup_begin_lr
        else:
            raise ValueError("Invalid warmup mode %s"%self.warmup_mode)

其中warmup_final_lr = base_lr

需要注意的是，因为没有实现__(self, num_update)方法，这个基类不能直接用来作为传给优化器的ls_scheduler参数，必须使用它的子类！

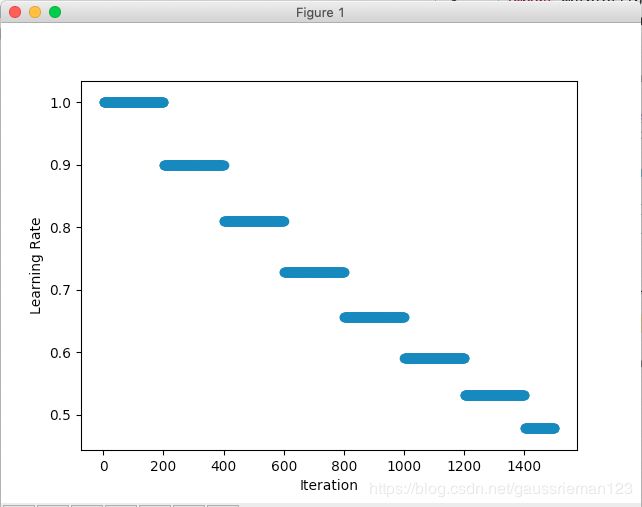
因子衰减FactorScheduler

初始化函数，在LRScheduler的基础上，增加了三个参数：

• step 每隔step次更新后调整学习率
• factor 调整因子，每次调整时乘以当前学习率得到调整后的学习率
• stop_factor_lr 最小学习率，达到这个值后不再更新学习率，可以避免过小学习率

调整策略：
$$lr=lr\ast factor$$

	def __init__(self, step, factor=1, stop_factor_lr=1e-8, base_lr=0.01,
                 warmup_steps=0, warmup_begin_lr=0, warmup_mode='linear'):
        super(FactorScheduler, self).__init__(base_lr, warmup_steps, warmup_begin_lr, warmup_mode)
        if step < 1:
            raise ValueError("Schedule step must be greater or equal than 1 round")
        if factor > 1.0:
            raise ValueError("Factor must be no more than 1 to make lr reduce")
        self.step = step
        self.factor = factor
        self.stop_factor_lr = stop_factor_lr
        self.count = 0

    def __call__(self, num_update):
        if num_update < self.warmup_steps:
            return self.get_warmup_lr(num_update)

        # NOTE: use while rather than if  (for continuing training via load_epoch)
        while num_update > self.count + self.step:
            self.count += self.step
            self.base_lr *= self.factor
            if self.base_lr < self.stop_factor_lr:
                self.base_lr = self.stop_factor_lr
                logging.info("Update[%d]: now learning rate arrived at %0.5e, will not "
                             "change in the future", num_update, self.base_lr)
            else:
                logging.info("Update[%d]: Change learning rate to %0.5e",
                             num_update, self.base_lr)
        return self.base_lr

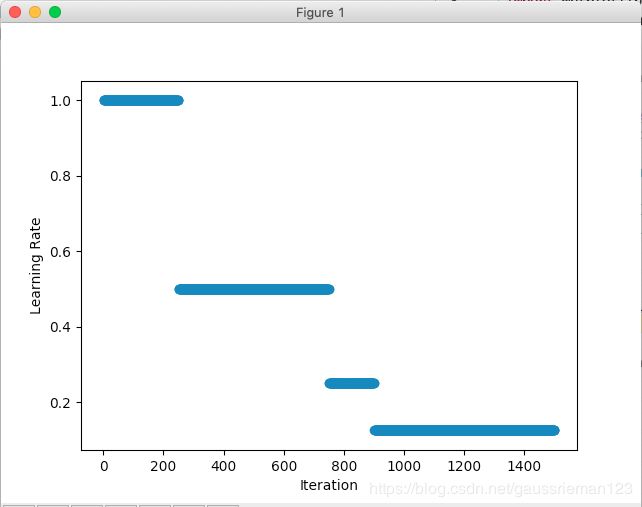
多因子衰减

与因子衰减相比，多因子衰减最大的区别是step不再是一个整数值，而是一个整数list，更新次数超过list中的一个值时，调整一次，区别只是在于调整的时机不一样：因子衰减，每隔固定次数调整；多因子衰减，每达到list中的更新次数才调整。

	def __init__(self, step, factor=1, base_lr=0.01, warmup_steps=0, warmup_begin_lr=0,
                 warmup_mode='linear'):
        super(MultiFactorScheduler, self).__init__(base_lr, warmup_steps,
                                                   warmup_begin_lr, warmup_mode)
        assert isinstance(step, list) and len(step) >= 1
        for i, _step in enumerate(step):
            if i != 0 and step[i] <= step[i-1]:
                raise ValueError("Schedule step must be an increasing integer list")
            if _step < 1:
                raise ValueError("Schedule step must be greater or equal than 1 round")
        if factor > 1.0:
            raise ValueError("Factor must be no more than 1 to make lr reduce")
        self.step = step
        self.cur_step_ind = 0
        self.factor = factor
        self.count = 0

    def __call__(self, num_update):
        if num_update < self.warmup_steps:
            return self.get_warmup_lr(num_update)

        # NOTE: use while rather than if  (for continuing training via load_epoch)
        while self.cur_step_ind <= len(self.step)-1:
            if num_update > self.step[self.cur_step_ind]:
                self.count = self.step[self.cur_step_ind]
                self.cur_step_ind += 1
                self.base_lr *= self.factor
                logging.info("Update[%d]: Change learning rate to %0.5e",
                             num_update, self.base_lr)
            else:
                return self.base_lr
        return self.base_lr

多项式调整

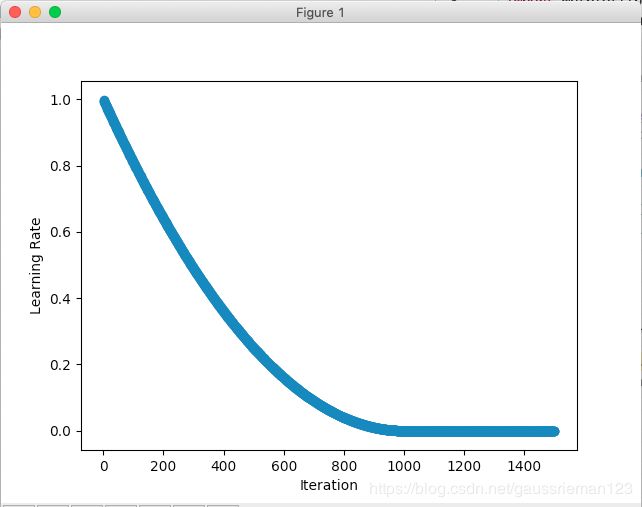
因子调整是用离散的数据来完成学习率的调整，很自然的能想到可以用连续函数来完成这一工作，而且由于学习率前面调整大，后面调整小，所以用底数位于(0,1)区间的幂函数来调整就非常合适。多项式策略就是用了幂函数来调整学习率。
下图，warmup_steps = 0，初始学习率为1，从0次更新就开始调整，到最大更新次数(max_update = 1000)之后不再变化，final_lr是最终学习率。

    def __init__(self, max_update, base_lr=0.01, pwr=2, final_lr=0,
                 warmup_steps=0, warmup_begin_lr=0, warmup_mode='linear'):
        super(PolyScheduler, self).__init__(base_lr, warmup_steps, warmup_begin_lr, warmup_mode)
        assert isinstance(max_update, int)
        if max_update < 1:
            raise ValueError("maximum number of updates must be strictly positive")
        self.power = pwr
        self.base_lr_orig = self.base_lr
        self.max_update = max_update
        self.final_lr = final_lr
        self.max_steps = self.max_update - self.warmup_steps

    def __call__(self, num_update):
        if num_update < self.warmup_steps:
            return self.get_warmup_lr(num_update)
        if num_update <= self.max_update:
            self.base_lr = self.final_lr + (self.base_lr_orig - self.final_lr) * \
                pow(1 - float(num_update - self.warmup_steps) / float(self.max_steps), self.power)
        return self.base_lr

余弦函数调整

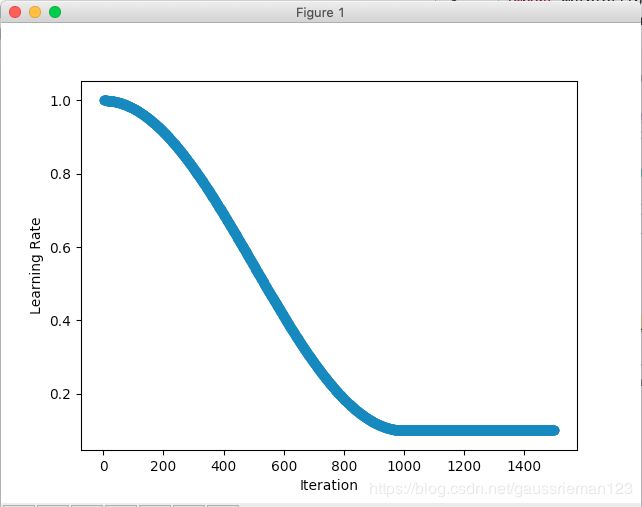
除了多项式函数，我们也可以利用余弦函数的单调性来完成学习率的调整,参数与多项式函数完全一样，只不过内部实现的函数完成了余弦函数：
初始学习率 1， 最终学习率 0.1， 最大更新次数 1000， warmup_steps 0：

	def __init__(self, max_update, base_lr=0.01, final_lr=0,
                 warmup_steps=0, warmup_begin_lr=0, warmup_mode='linear'):
        super(CosineScheduler, self).__init__(base_lr, warmup_steps, warmup_begin_lr, warmup_mode)
        assert isinstance(max_update, int)
        if max_update < 1:
            raise ValueError("maximum number of updates must be strictly positive")
        self.base_lr_orig = base_lr
        self.max_update = max_update
        self.final_lr = final_lr
        self.max_steps = self.max_update - self.warmup_steps

    def __call__(self, num_update):
        if num_update < self.warmup_steps:
            return self.get_warmup_lr(num_update)
        if num_update <= self.max_update:
            self.base_lr = self.final_lr + (self.base_lr_orig - self.final_lr) * \
                (1 + cos(pi * (num_update - self.warmup_steps) / self.max_steps)) / 2
        return self.base_lr

参考

https://zhuanlan.zhihu.com/p/31424275
http://mxnet.incubator.apache.org/versions/master/tutorials/gluon/learning_rate_schedules.html