遥感图像增强方法应用
分享一下我老师大神的人工智能教程！零基础，通俗易懂！http://blog.csdn.net/jiangjunshow
也欢迎大家转载本篇文章。分享知识，造福人民，实现我们中华民族伟大复兴！
（广西气象减灾研究所 广西南宁 530022）
1、引 言
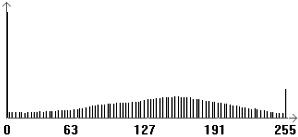
人类从眼睛获取信息占人体器官获取信息的90%以上，虽然人眼能看到很多东西，但其实我们看到的只是波长为0.38～0.8μm可见光部分，是电磁波的极小部分。遥感技术的应用是人类视觉在波谱范围上的扩展和从物体表面向内部的延伸。即使在可见光部分，人眼可区分的色彩约三千多种，但对于黑白图像，人眼能区分的灰度级只有二三十个；而在非可见光波段，需要将原始图像的灰度值转换到0～255灰度区间才有利于人眼观察。但是如果我们以256个灰度级来描述一幅黑白遥感图像，我们获得的原始图像的灰度值很难均匀分布在0～255之间，而是常常集中在某一段灰度范围之内，图像的反差小，对比度差，不利于人眼的分辨[1]，所以我们需要对遥感图像进行增强处理。
2、遥感图像增强算法
图像增强指利用各种数学方法和变换算法提高图像中的对象与非对象的对比度与图像清晰度，对象指所研究目标，非对象指对象以外的背景，从而突出人或其它接收系统所感兴趣的部分，而遥感图像增强则指用各种数学方法和变换算法提高某灰度区域的反差、对比度与清晰度，从而提高图像显示的信息量，使图像有利于人眼分辨。
图像增强的方法主要又两大类：空间域法和频率域法。空间域法主要是在空间域直接对图像的灰度系数进行处理；频率域法是在图像的某种变化域内，对图像的变化系数值进行某种修正，然后通过逆变换获得增强图像。频率域法属于间接增强的方法，低通滤波、同态图像增强均属于该类；空间域法属于直接增强的方法，它又可分为灰度级校正、灰度变换和直方图修正，直方图均衡属于空间域单点增强的直方图修正法。下面介绍的几种方法属于空间域法。
2.1 基于线性拉伸的图像增强
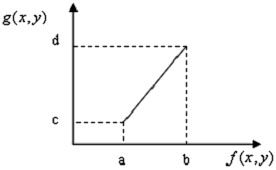
线性拉伸[1]是将范围为[a，b]数字图像的灰度f（x，y）变换为范围为[c，d]的灰度g（x，y），如图1所示。
图2.1 灰度输入输出变换简图
线性拉伸的变换数学公式为：
（1）
如果遥感数据的f（x，y）的范围是[a，b]，那么要将遥感数据生成图像并且在计算机上显示出来，则需要将f（x，y）变换为g（x，y），其中g（x，y）的范围为[0，255]，则其数学变换公式为：
使用线性拉伸增强对遥感数据进行，增强后的图像直方图跟原始数据的直方图是相似的。
2.2 基于分段线性拉伸的图像增强
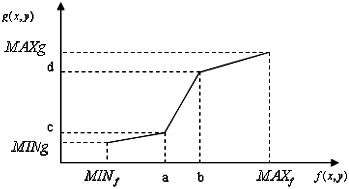
分段线性增强[2]是将图像灰度f（x，y）的区间分割为若干区间，然后对每个区间进行线性拉伸，常用的是分三段线性变换，假设原图像灰度的范围为（MINf，MAXf），则把图像分割为三段（MINf，a）、（a，b）、（b，MAXf），分别拉伸到对应三个区间（MINg，c）、（c，d）、（d，MAXg），通过调节a，b，c，d可以对任意区间的分线段斜率进行调节，如图2所示。
图2.2 分段增强示意图
对于遥感数据，遥感数据的范围为（MINf，MAXf），分为三段（MINf，a）、（a，b）、（b，MAXf）分别做线性增强到（0，c）、（c，d）、（d，255）三个灰度区间，变换公式为：
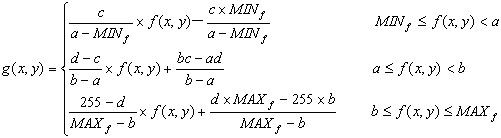（3）
采用分段增强，可以将感兴趣或者重要的灰度区域拉伸，使该区域的信息量增大，同时抑制了不感兴趣或者不重要的区域。
2.3 基于直方图均衡的图像增强
直方图均衡也称为灰度均衡[3]，目的是通过点运算，使得输入图像转换为直方图是平的图像（即每个灰度级上都有相同的像素点个数）。
按照概率密度函数（归一化到单位面积的直方图）的定义：
（4）
其中ρ（x）概率密度函数，为H（x）为图像的直方图，A0为图像的面积。
假设转换前图像的概率密度函数为
，转换后图像的概率密度函数为
，转换函数为s=f（r）。我们可以得到：
（5）
为了使转换后图像的概率密度曲线是平的，即＝1，则必须满足：
（6）
等式两边对r积分，可得：
（7）
转换公式s称为图像的累积分布函数。
对于没有归一化的情况，只要乘以最大的灰度MAXg，即得到灰度均衡的转换公式：
（8）
对于离散的遥感数据，如果其像元灰度值DA的范围为（MINf，MAXf），转换的灰度范围为（0，255），则可得转换的公式为：
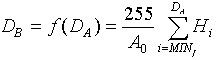（9）
式中，Hi为遥感数据中值为i的像元个数，DB为像元灰度DA经过转换后得到的灰度。使用直方图均衡增强，使得图像的直方图呈均匀分布，此时图像所包含的信息量为最大；同时，若一幅图像的直方图呈均匀分布，人眼观看图像时，就有全图清晰、明快的感觉。
3、几种增强方法的效果对比
3.1 实际开发应用
基于上述算法，在WINDOWS XP操作系统，VC开发环境下进行开发试验，通过一副NOAA AVHRR数据的二通道数据将上述算法进行比较。比较效果如下：
图3.1 二通道数据直方图
|
|
|
图3.2 基于线性拉伸的遥感图像
|
图3.3 线性拉伸后的灰度直方图
|
|
|
|
图3.4 基于分段增强的遥感图像
|
图3.5 分段增强后的灰度直方图
|
|
|
|
图3.6 基于直方图均衡的遥感图像
|
图3.7 均衡增强后的灰度直方图
|
3.2 效果对比分析
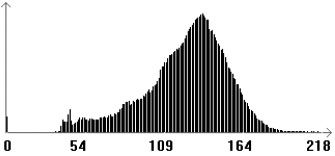
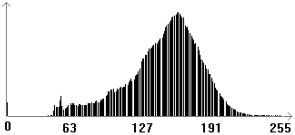
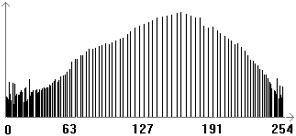
图3.1为AVHRR二通道数据直方图。线性拉伸后效果如图3.2，灰度直方图如图3.3，进行线性拉伸后的灰度直方图与数据直方图是基本相似，但是图像整体对比度不强。
图3.4是经过分段增强后的图像，其灰度直方图如图3.5所示，被增强的数据段的灰度分布于0～254的灰度等级，而被忽略的数据的灰度则为0或者255，分段增强能够很好的将感兴趣的数据段增强出来，充分显示其包含的信息。
图3.6是经过直方图均衡增强的图像，其灰度直方图如图3.7所示，直方图均衡增强后图像的特点是整体对比度很强，图像比较美观，但是会造成灰度的“吞噬”使遥感图像信息有所丢失，特别是当原始遥感数据的质量比较差、数据动态范围小、直方图分布极不均匀时，进行直方图均衡增强运算或者进一步进行直方图规定化，变换后的图像层次感更差，更易丢失信息[4]。
4、结束语
卫星遥感在生态环境监测中发挥着重要的作用，其影像图的质量直接影响监测的效果以及产品的质量，利用数字图像处理技术，能有效提高卫星遥感影像图的质量。上述介绍气象卫星的图像处理技术和方法，已被应用于“基于MODIS卫星数据的广西洪涝、干旱、火情遥感监测业务平台”研发中，并取得了令人满意的效果。
参 考 文 献
[1] 殷年.基于线性拉伸的遥感图像处理.光电子技术与信息，1998
[2] 黄涛.数字图像的增强.肇庆学院学报，2004，4，23～27
[3] 何斌、马天予、王运坚，朱红莲.Visual C++数字图像处理[M].北京：人民邮电出版社，2002
[4] 李耀辉、刘保军.基于直方图均衡的图像增强.华北科技学院学报，2003
给我老师的人工智能教程打call！http://blog.csdn.net/jiangjunshow
新的改变
我们对Markdown编辑器进行了一些功能拓展与语法支持，除了标准的Markdown编辑器功能，我们增加了如下几点新功能，帮助你用它写博客：
- 全新的界面设计 ，将会带来全新的写作体验；
- 在创作中心设置你喜爱的代码高亮样式，Markdown 将代码片显示选择的高亮样式 进行展示；
- 增加了 图片拖拽 功能，你可以将本地的图片直接拖拽到编辑区域直接展示；
- 全新的 KaTeX数学公式 语法；
- 增加了支持甘特图的mermaid语法1 功能；
- 增加了 多屏幕编辑 Markdown文章功能；
- 增加了 焦点写作模式、预览模式、简洁写作模式、左右区域同步滚轮设置 等功能，功能按钮位于编辑区域与预览区域中间；
- 增加了 检查列表 功能。
功能快捷键
撤销：Ctrl/Command + Z
重做：Ctrl/Command + Y
加粗：Ctrl/Command + B
斜体：Ctrl/Command + I
标题：Ctrl/Command + Shift + H
无序列表：Ctrl/Command + Shift + U
有序列表：Ctrl/Command + Shift + O
检查列表：Ctrl/Command + Shift + C
插入代码：Ctrl/Command + Shift + K
插入链接：Ctrl/Command + Shift + L
插入图片：Ctrl/Command + Shift + G
合理的创建标题，有助于目录的生成
直接输入1次#，并按下space后，将生成1级标题。
输入2次#，并按下space后，将生成2级标题。
以此类推，我们支持6级标题。有助于使用TOC语法后生成一个完美的目录。
如何改变文本的样式
强调文本 强调文本
加粗文本 加粗文本
标记文本
删除文本
引用文本
H2O is是液体。
210 运算结果是 1024.
插入链接与图片
链接: link.
图片: 
带尺寸的图片:
当然，我们为了让用户更加便捷，我们增加了图片拖拽功能。
如何插入一段漂亮的代码片
去博客设置页面，选择一款你喜欢的代码片高亮样式，下面展示同样高亮的 代码片.
// An highlighted block var foo = 'bar'; 生成一个适合你的列表
- 项目
- 项目
- 项目
- 项目
- 项目1
- 项目2
- 项目3
- 计划任务
- 完成任务
创建一个表格
一个简单的表格是这么创建的：
| 项目 | Value |
|---|---|
| 电脑 | $1600 |
| 手机 | $12 |
| 导管 | $1 |
设定内容居中、居左、居右
使用:---------:居中
使用:----------居左
使用----------:居右
| 第一列 | 第二列 | 第三列 |
|---|---|---|
| 第一列文本居中 | 第二列文本居右 | 第三列文本居左 |
SmartyPants
SmartyPants将ASCII标点字符转换为“智能”印刷标点HTML实体。例如：
| TYPE | ASCII | HTML |
|---|---|---|
| Single backticks | 'Isn't this fun?' |
‘Isn’t this fun?’ |
| Quotes | "Isn't this fun?" |
“Isn’t this fun?” |
| Dashes | -- is en-dash, --- is em-dash |
– is en-dash, — is em-dash |
创建一个自定义列表
- Markdown
- Text-to- HTML conversion tool
- Authors
- John
- Luke
如何创建一个注脚
一个具有注脚的文本。2
注释也是必不可少的
Markdown将文本转换为 HTML。
KaTeX数学公式
您可以使用渲染LaTeX数学表达式 KaTeX:
Gamma公式展示 Γ ( n ) = ( n − 1 ) ! ∀ n ∈ N \Gamma(n) = (n-1)!\quad\forall n\in\mathbb N Γ(n)=(n−1)!∀n∈N 是通过欧拉积分
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t . \Gamma(z) = \int_0^\infty t^{z-1}e^{-t}dt\,. Γ(z)=∫0∞tz−1e−tdt.
你可以找到更多关于的信息 LaTeX 数学表达式here.
新的甘特图功能，丰富你的文章
gantt
dateFormat YYYY-MM-DD
title Adding GANTT diagram functionality to mermaid
section 现有任务
已完成 :done, des1, 2014-01-06,2014-01-08
进行中 :active, des2, 2014-01-09, 3d
计划一 : des3, after des2, 5d
计划二 : des4, after des3, 5d
- 关于 甘特图 语法，参考 这儿,
UML 图表
可以使用UML图表进行渲染。 Mermaid. 例如下面产生的一个序列图：:
这将产生一个流程图。:
- 关于 Mermaid 语法，参考 这儿,
FLowchart流程图
我们依旧会支持flowchart的流程图：
- 关于 Flowchart流程图 语法，参考 这儿.
导出与导入
导出
如果你想尝试使用此编辑器, 你可以在此篇文章任意编辑。当你完成了一篇文章的写作, 在上方工具栏找到 文章导出 ，生成一个.md文件或者.html文件进行本地保存。
导入
如果你想加载一篇你写过的.md文件或者.html文件，在上方工具栏可以选择导入功能进行对应扩展名的文件导入，
继续你的创作。
mermaid语法说明 ↩︎
注脚的解释 ↩︎