十八、图算法之最短路径

最短路径

这里基于的是加权有向图的讨论，而且是单源最短路径问题。我们称为最短路径的结果是一棵最短路径树。

给定一幅加权有向图和一个顶点s，以s为起点的一棵最短路径树是图的一幅子图，它包含s和从s可达的所有顶点。这棵有向树的根节点为s，树的每条路径（到每个点的每条路径）都是有向图中的一条最短路径。

加权有向图的数据结构

有向边类：

public class EdgeWeightedDigraph {
    private static final String NEWLINE = System.getProperty("line.separator");

    private final int V;                // number of vertices in this digraph
    private int E;                      // number of edges in this digraph
    private Bag[] adj;    // adj[v] = adjacency list for vertex v
    private int[] indegree;             // indegree[v] = indegree of vertex v
    public EdgeWeightedDigraph(int V) {
        if (V < 0) throw new IllegalArgumentException("Number of vertices in a Digraph must be nonnegative");
        this.V = V;
        this.E = 0;
        this.indegree = new int[V];
        adj = (Bag[]) new Bag[V];
        for (int v = 0; v < V; v++)
            adj[v] = new Bag();
    }
    public EdgeWeightedDigraph(int V, int E) {
        this(V);
        if (E < 0) throw new IllegalArgumentException("Number of edges in a Digraph must be nonnegative");
        for (int i = 0; i < E; i++) {
            int v = StdRandom.uniform(V);
            int w = StdRandom.uniform(V);
            double weight = .01 * StdRandom.uniform(100);
            DirectedEdge e = new DirectedEdge(v, w, weight);
            addEdge(e);
        }
    }
    public EdgeWeightedDigraph(In in) {
        this(in.readInt());
        int E = in.readInt();
        if (E < 0) throw new IllegalArgumentException("Number of edges must be nonnegative");
        for (int i = 0; i < E; i++) {
            int v = in.readInt();
            int w = in.readInt();
            if (v < 0 || v >= V) throw new IndexOutOfBoundsException("vertex " + v + " is not between 0 and " + (V-1));
            if (w < 0 || w >= V) throw new IndexOutOfBoundsException("vertex " + w + " is not between 0 and " + (V-1));
            double weight = in.readDouble();
            addEdge(new DirectedEdge(v, w, weight));
        }
    }
    public EdgeWeightedDigraph(EdgeWeightedDigraph G) {
        this(G.V());
        this.E = G.E();
        for (int v = 0; v < G.V(); v++)
            this.indegree[v] = G.indegree(v);
        for (int v = 0; v < G.V(); v++) {
            // reverse so that adjacency list is in same order as original
            Stack reverse = new Stack();
            for (DirectedEdge e : G.adj[v]) {
                reverse.push(e);
            }
            for (DirectedEdge e : reverse) {
                adj[v].add(e);
            }
        }
    }
    public int V() {
        return V;
    }
    public int E() {
        return E;
    }
    // throw an IndexOutOfBoundsException unless 0 <= v < V
    private void validateVertex(int v) {
        if (v < 0 || v >= V)
            throw new IndexOutOfBoundsException("vertex " + v + " is not between 0 and " + (V-1));
    }
    public void addEdge(DirectedEdge e) {
        int v = e.from();
        int w = e.to();
        validateVertex(v);
        validateVertex(w);
        adj[v].add(e);
        indegree[w]++;
        E++;
    }
    public Iterable adj(int v) {
        validateVertex(v);
        return adj[v];
    }
    public int outdegree(int v) {
        validateVertex(v);
        return adj[v].size();
    }
    public int indegree(int v) {
        validateVertex(v);
        return indegree[v];
    }
    public Iterable edges() {
        Bag list = new Bag();
        for (int v = 0; v < V; v++) {
            for (DirectedEdge e : adj(v)) {
                list.add(e);
            }
        }
        return list;
    } 
    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(V + " " + E + NEWLINE);
        for (int v = 0; v < V; v++) {
            s.append(v + ": ");
            for (DirectedEdge e : adj[v]) {
                s.append(e + "  ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }
}

---

Dijstra算法（有向，无负边）

要求权重非负，算法很简单，不再赘述
复杂度： 空间与V成正比，时间与ElogV成正比
内部使用了索引优先队列

public class DijkstraSP {
    private double[] distTo;          // distTo[v] = distance  of shortest s->v path
    private DirectedEdge[] edgeTo;    // edgeTo[v] = last edge on shortest s->v path
    private IndexMinPQ pq;    // priority queue of vertices
    public DijkstraSP(EdgeWeightedDigraph G, int s) {
        for (DirectedEdge e : G.edges()) {
            if (e.weight() < 0)
                throw new IllegalArgumentException("edge " + e + " has negative weight");
        }
        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;
        // relax vertices in order of distance from s
        pq = new IndexMinPQ(G.V());
        pq.insert(s, distTo[s]);
        while (!pq.isEmpty()) {
            int v = pq.delMin();
            for (DirectedEdge e : G.adj(v))
                relax(e);
        }

        // check optimality conditions
        assert check(G, s);
    }
    // relax edge e and update pq if changed
    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
            if (pq.contains(w)) pq.decreaseKey(w, distTo[w]);
            else                pq.insert(w, distTo[w]);
        }
    }
    public double distTo(int v) {
        return distTo[v];
    }
    public boolean hasPathTo(int v) {
        return distTo[v] < Double.POSITIVE_INFINITY;
    }
    public Iterable pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack path = new Stack();
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
            path.push(e);
        }
        return path;
    }
    // check optimality conditions:
    // (i) for all edges e:            distTo[e.to()] <= distTo[e.from()] + e.weight()
    // (ii) for all edge e on the SPT: distTo[e.to()] == distTo[e.from()] + e.weight()
    private boolean check(EdgeWeightedDigraph G, int s) {
        // check that edge weights are nonnegative
        for (DirectedEdge e : G.edges()) {
            if (e.weight() < 0) {
                System.err.println("negative edge weight detected");
                return false;
            }
        }
        // check that distTo[v] and edgeTo[v] are consistent
        if (distTo[s] != 0.0 || edgeTo[s] != null) {
            System.err.println("distTo[s] and edgeTo[s] inconsistent");
            return false;
        }
        for (int v = 0; v < G.V(); v++) {
            if (v == s) continue;
            if (edgeTo[v] == null && distTo[v] != Double.POSITIVE_INFINITY) {
                System.err.println("distTo[] and edgeTo[] inconsistent");
                return false;
            }
        }
        // check that all edges e = v->w satisfy distTo[w] <= distTo[v] + e.weight()
        for (int v = 0; v < G.V(); v++) {
            for (DirectedEdge e : G.adj(v)) {
                int w = e.to();
                if (distTo[v] + e.weight() < distTo[w]) {
                    System.err.println("edge " + e + " not relaxed");
                    return false;
                }
            }
        }
        // check that all edges e = v->w on SPT satisfy distTo[w] == distTo[v] + e.weight()
        for (int w = 0; w < G.V(); w++) {
            if (edgeTo[w] == null) continue;
            DirectedEdge e = edgeTo[w];
            int v = e.from();
            if (w != e.to()) return false;
            if (distTo[v] + e.weight() != distTo[w]) {
                System.err.println("edge " + e + " on shortest path not tight");
                return false;
            }
        }
        return true;
    }
}

---

无环加权有向图中的最短路径算法

无环，能有负边，比Dijstra算法快
按照拓扑排序（详见之前博客）更新权值

按照拓扑排序更新权值，就能在和E+V成正比的时间内解决无环加权有向图的电源最短路径问题

public class AcyclicSP {
    private double[] distTo;         // distTo[v] = distance  of shortest s->v path
    private DirectedEdge[] edgeTo;   // edgeTo[v] = last edge on shortest s->v path
    public AcyclicSP(EdgeWeightedDigraph G, int s) {
        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        // visit vertices in toplogical order
        Topological topological = new Topological(G);
        if (!topological.hasOrder())
            throw new IllegalArgumentException("Digraph is not acyclic.");
        for (int v : topological.order()) {
            for (DirectedEdge e : G.adj(v))
                relax(e);
        }
    }
    // relax edge e
    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
        }       
    }
    public double distTo(int v) {
        return distTo[v];
    }
    public boolean hasPathTo(int v) {
        return distTo[v] < Double.POSITIVE_INFINITY;
    }
    public Iterable pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack path = new Stack();
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
            path.push(e);
        }
        return path;
    }
}

---

无环加权有向图中的最长路径算法

放松边的那个符号反过来就行了，初始化要改成负无穷

public class AcyclicLP {
    private double[] distTo;          // distTo[v] = distance  of longest s->v path
    private DirectedEdge[] edgeTo;    // edgeTo[v] = last edge on longest s->v path
    public AcyclicLP(EdgeWeightedDigraph G, int s) {
        distTo = new double[G.V()];
        edgeTo = new DirectedEdge[G.V()];
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.NEGATIVE_INFINITY;
        distTo[s] = 0.0;
        // relax vertices in toplogical order
        Topological topological = new Topological(G);
        if (!topological.hasOrder())
            throw new IllegalArgumentException("Digraph is not acyclic.");
        for (int v : topological.order()) {
            for (DirectedEdge e : G.adj(v))
                relax(e);
        }
    }
    // relax edge e, but update if you find a *longer* path
    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        if (distTo[w] < distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
        }       
    }
    public double distTo(int v) {
        return distTo[v];
    }
    public boolean hasPathTo(int v) {
        return distTo[v] > Double.NEGATIVE_INFINITY;
    }
    public Iterable pathTo(int v) {
        if (!hasPathTo(v)) return null;
        Stack path = new Stack();
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
            path.push(e);
        }
        return path;
    }
}

一个应用：平行任务调度

优先级限制下的平行任务调度

任务有优先级关系，有些任务必须在其他任务之前完成，单CPU的任务调度其实就是求拓扑排序就行了。平行任务调度则是多个CPU执行，完成时间最短的调度为最优。
平行任务调度相当于求一个最长路径（求“最长路径”是指求优先级限制图的最长路径，比这个更短的路径是满足不了优先级限制的，所以要求最长。而且最长的都能跑，并行的其他短的肯定也能跑），这个图的构造如下：

public class CPM {
    // this class cannot be instantiated
    private CPM() { }
    public static void main(String[] args) {

        // number of jobs
        int N = StdIn.readInt();

        // source and sink
        int source = 2*N;
        int sink   = 2*N + 1;
        // build network
        EdgeWeightedDigraph G = new EdgeWeightedDigraph(2*N + 2);
        for (int i = 0; i < N; i++) {
            double duration = StdIn.readDouble();
            G.addEdge(new DirectedEdge(source, i, 0.0));
            G.addEdge(new DirectedEdge(i+N, sink, 0.0));
            G.addEdge(new DirectedEdge(i, i+N,    duration));

            // precedence constraints
            int M = StdIn.readInt();
            for (int j = 0; j < M; j++) {
                int precedent = StdIn.readInt();
                G.addEdge(new DirectedEdge(N+i, precedent, 0.0));
            }
        }
        // compute longest path
        AcyclicLP lp = new AcyclicLP(G, source);

        // print results
        StdOut.println(" job   start  finish");
        StdOut.println("--------------------");
        for (int i = 0; i < N; i++) {
            StdOut.printf("%4d %7.1f %7.1f\n", i, lp.distTo(i), lp.distTo(i+N));
        }
        StdOut.printf("Finish time: %7.1f\n", lp.distTo(sink));
    }
}

相对最后期限下的并行任务调度

再加一个限制：deadline，也就是截止时间限制（相对某个任务的截止时间，比如不能相差多少秒）。方法是同上面一样构造图，同时会添加负权重边，再将所有边取反，然后求最短路径，最短路径存在则可行（没有负权重环就是可行的调度）。

---

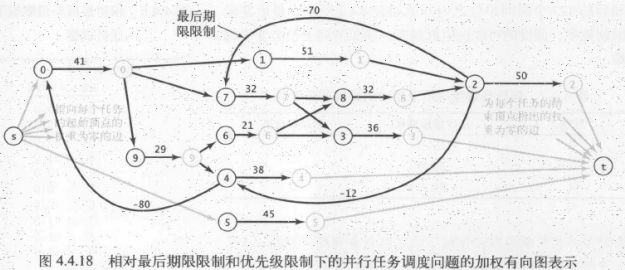
一般有向加权图的最短路径问题

考虑有环也可能负边的最短路径问题

负权重环会导致绕圈现象，因此负权重环存在求不出最短路径

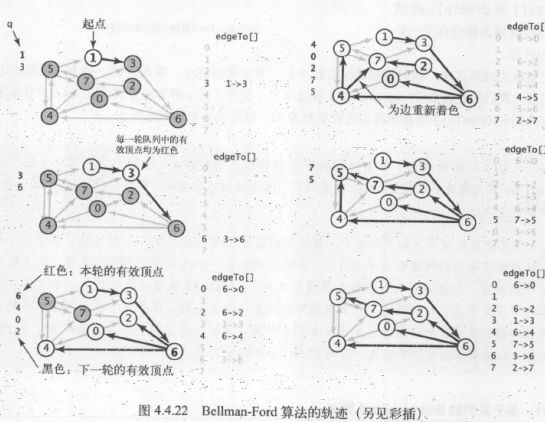
解决路径没有负权重环的最短路径算法：Bellman-ford算法


过程：

下面讨论改进版本：

基于队列的Bellman-Ford算法

public class BellmanFordSP {
    private double[] distTo;               // distTo[v] = distance  of shortest s->v path
    private DirectedEdge[] edgeTo;         // edgeTo[v] = last edge on shortest s->v path
    private boolean[] onQueue;             // onQueue[v] = is v currently on the queue?
    private Queue queue;          // queue of vertices to relax
    private int cost;                      // number of calls to relax()
    private Iterable cycle;  // negative cycle (or null if no such cycle)
    public BellmanFordSP(EdgeWeightedDigraph G, int s) {
        distTo  = new double[G.V()];
        edgeTo  = new DirectedEdge[G.V()];
        onQueue = new boolean[G.V()];
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        // Bellman-Ford algorithm
        queue = new Queue();
        queue.enqueue(s);
        onQueue[s] = true;
        while (!queue.isEmpty() && !hasNegativeCycle()) {
            int v = queue.dequeue();
            onQueue[v] = false;
            relax(G, v);
        }

        assert check(G, s);
    }

    // relax vertex v and put other endpoints on queue if changed
    private void relax(EdgeWeightedDigraph G, int v) {
        for (DirectedEdge e : G.adj(v)) {
            int w = e.to();
            if (distTo[w] > distTo[v] + e.weight()) {
                distTo[w] = distTo[v] + e.weight();
                edgeTo[w] = e;
                if (!onQueue[w]) {
                    queue.enqueue(w);
                    onQueue[w] = true;
                }
            }
            if (cost++ % G.V() == 0) {
                findNegativeCycle();
                if (hasNegativeCycle()) return;  // found a negative cycle
            }
        }
    }
    public boolean hasNegativeCycle() {
        return cycle != null;
    }
    public Iterable negativeCycle() {
        return cycle;
    }

    // by finding a cycle in predecessor graph
    private void findNegativeCycle() {
        int V = edgeTo.length;
        EdgeWeightedDigraph spt = new EdgeWeightedDigraph(V);
        for (int v = 0; v < V; v++)
            if (edgeTo[v] != null)
                spt.addEdge(edgeTo[v]);

        EdgeWeightedDirectedCycle finder = new EdgeWeightedDirectedCycle(spt);
        cycle = finder.cycle();
    }
    public double distTo(int v) {
        if (hasNegativeCycle())
            throw new UnsupportedOperationException("Negative cost cycle exists");
        return distTo[v];
    }
    public boolean hasPathTo(int v) {
        return distTo[v] < Double.POSITIVE_INFINITY;
    }
    public Iterable pathTo(int v) {
        if (hasNegativeCycle())
            throw new UnsupportedOperationException("Negative cost cycle exists");
        if (!hasPathTo(v)) return null;
        Stack path = new Stack();
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
            path.push(e);
        }
        return path;
    }
    // check optimality conditions: either 
    // (i) there exists a negative cycle reacheable from s
    //     or 
    // (ii)  for all edges e = v->w:            distTo[w] <= distTo[v] + e.weight()
    // (ii') for all edges e = v->w on the SPT: distTo[w] == distTo[v] + e.weight()
    private boolean check(EdgeWeightedDigraph G, int s) {

        // has a negative cycle
        if (hasNegativeCycle()) {
            double weight = 0.0;
            for (DirectedEdge e : negativeCycle()) {
                weight += e.weight();
            }
            if (weight >= 0.0) {
                System.err.println("error: weight of negative cycle = " + weight);
                return false;
            }
        }
        // no negative cycle reachable from source
        else {

            // check that distTo[v] and edgeTo[v] are consistent
            if (distTo[s] != 0.0 || edgeTo[s] != null) {
                System.err.println("distanceTo[s] and edgeTo[s] inconsistent");
                return false;
            }
            for (int v = 0; v < G.V(); v++) {
                if (v == s) continue;
                if (edgeTo[v] == null && distTo[v] != Double.POSITIVE_INFINITY) {
                    System.err.println("distTo[] and edgeTo[] inconsistent");
                    return false;
                }
            }

            // check that all edges e = v->w satisfy distTo[w] <= distTo[v] + e.weight()
            for (int v = 0; v < G.V(); v++) {
                for (DirectedEdge e : G.adj(v)) {
                    int w = e.to();
                    if (distTo[v] + e.weight() < distTo[w]) {
                        System.err.println("edge " + e + " not relaxed");
                        return false;
                    }
                }
            }

            // check that all edges e = v->w on SPT satisfy distTo[w] == distTo[v] + e.weight()
            for (int w = 0; w < G.V(); w++) {
                if (edgeTo[w] == null) continue;
                DirectedEdge e = edgeTo[w];
                int v = e.from();
                if (w != e.to()) return false;
                if (distTo[v] + e.weight() != distTo[w]) {
                    System.err.println("edge " + e + " on shortest path not tight");
                    return false;
                }
            }
        }

        StdOut.println("Satisfies optimality conditions");
        StdOut.println();
        return true;
    }
}

里面有一个EdgeWeightedDirectedCycle 类：

public class EdgeWeightedDirectedCycle {
    private boolean[] marked;             // marked[v] = has vertex v been marked?
    private DirectedEdge[] edgeTo;        // edgeTo[v] = previous edge on path to v
    private boolean[] onStack;            // onStack[v] = is vertex on the stack?
    private Stack cycle;    // directed cycle (or null if no such cycle)
    public EdgeWeightedDirectedCycle(EdgeWeightedDigraph G) {
        marked  = new boolean[G.V()];
        onStack = new boolean[G.V()];
        edgeTo  = new DirectedEdge[G.V()];
        for (int v = 0; v < G.V(); v++)
            if (!marked[v]) dfs(G, v);

        // check that digraph has a cycle
        assert check(G);
    }
    // check that algorithm computes either the topological order or finds a directed cycle
    private void dfs(EdgeWeightedDigraph G, int v) {
        onStack[v] = true;
        marked[v] = true;
        for (DirectedEdge e : G.adj(v)) {
            int w = e.to();

            // short circuit if directed cycle found
            if (cycle != null) return;

            //found new vertex, so recur
            else if (!marked[w]) {
                edgeTo[w] = e;
                dfs(G, w);
            }

            // trace back directed cycle
            else if (onStack[w]) {
                cycle = new Stack();
                while (e.from() != w) {
                    cycle.push(e);
                    e = edgeTo[e.from()];
                }
                cycle.push(e);
                return;
            }
        }

        onStack[v] = false;
    }
    public boolean hasCycle() {
        return cycle != null;
    }
    public Iterable cycle() {
        return cycle;
    }


    // certify that digraph is either acyclic or has a directed cycle
    private boolean check(EdgeWeightedDigraph G) {
        // edge-weighted digraph is cyclic
        if (hasCycle()) {
            // verify cycle
            DirectedEdge first = null, last = null;
            for (DirectedEdge e : cycle()) {
                if (first == null) first = e;
                if (last != null) {
                    if (last.to() != e.from()) {
                        System.err.printf("cycle edges %s and %s not incident\n", last, e);
                        return false;
                    }
                }
                last = e;
            }
            if (last.to() != first.from()) {
                System.err.printf("cycle edges %s and %s not incident\n", last, first);
                return false;
            }
        }
        return true;
    }

}

套汇

一种货币换成另一种货币，然后再换回来（换过去和换回来的中间货币可能不一样）造成了一定利润空间，称为套汇。