三个matlab练习程序 -Moravec算子- 各向异性扩散- TV模型图像修复
时间太久忘记是我自己整理的还是参照了一下别人的,我先设为原创,如有侵权请告知。
matlab练习程序(Moravec算子)
这个算子算是图像历史上第一个特征点提取算法了,1977年提出的,很简单,拿来练手很合适。
算法原理如下:
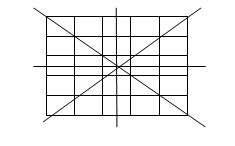
1.选取一个合理的邻域遍历图像,这里是5*5邻域的。在邻域中依次计算,垂直,水平,对角与反对角四个相邻像素灰度的差的平方和,作为该邻域特征值。
大致就是下面这个样子:
公式:
这里k是窗口的半径。
2.从四个特征值中选最小的值作为该像素初次候选特征值。
公式:
![]()
3.设定一个阈值,将大于该阈值初次候选特征值的选为二次候选特征值。
4.设定一个邻域,将该邻域最大的二次候选特征值作为最终要选择的特征值。
原图:
处理后:
matlab代码如下:
![]()
clear all;close all;clc
img=double(imread('lena.jpg'));
[h w]=size(img);
imshow(img,[])
imgn=zeros(h,w);
n=4;
for y=1+n:h-n
for x=1+n:w-n
sq=img(y-n:y+n,x-n:x+n);
V=zeros(1,4);
for i=2:2*n+1 %垂直,水平,对角,反对角四个方向领域灰度差的平方和
V(1)=V(1)+(sq(i,n+1)-sq(i-1,n+1))^2;
V(2)=V(2)+(sq(n+1,i)-sq(n+1,i-1))^2;
V(3)=V(3)+(sq(i,i)-sq(i-1,i-1))^2;
V(4)=V(4)+(sq(i,(2*n+1)-(i-1))-sq(i-1,(2*n+1)-(i-2)))^2;
end
pix=min(V); %四个方向中选最小值
imgn(y,x)=pix;
end
end
T=mean(imgn(:)); %设阈值,小于均值置零
ind=find(imgn
imgn(ind)=0;
for y=1+n:h-n %选局部最大且非零值作为特征点
for x=1+n:w-n
sq=imgn(y-n:y+n,x-n:x+n);
if max(sq(:))==imgn(y,x) && imgn(y,x)~=0
img(y,x)=255;
end
end
end
figure;
imshow(img,[]);
![]()
算法整个过程还是很简单的,练习一下,顺便祭下这个特征值开山算法。
matlab练习程序(各向异性扩散)
主要是用来平滑图像的,克服了高斯模糊的缺陷,各向异性扩散在平滑图像时是保留图像边缘的(和双边滤波很像)。
通常我们有将图像看作矩阵的,看作图的,看作随机过程的,记得过去还有看作力场的。
这次新鲜,将图像看作热量场了。每个像素看作热流,根据当前像素和周围像素的关系,来确定是否要向周围扩散。比如某个邻域像素和当前像素差别较大,则代表这个邻域像素很可能是个边界,那么当前像素就不向这个方向扩散了,这个边界也就得到保留了。
先看下效果吧:
具体的推导公式都是热学上的,自己也不太熟悉,感兴趣的可以去看原论文,引用量超7000吶。
我这里只介绍一下最终结论用到的公式。
主要迭代方程如下:
I就是图像了,因为是个迭代公式,所以有迭代次数t。
四个散度公式是在四个方向上对当前像素求偏导,news就是东南西北嘛,公式如下:
而cN/cS/cE/cW则代表四个方向上的导热系数,边界的导热系数都是小的。公式如下:
最后整个公式需要先前设置的参数主要有三个,迭代次数t,根据情况设置;导热系数相关的k,取值越大越平滑,越不易保留边缘;lambda同样也是取值越大越平滑。
最后是matlab代码:
![]()
clear all;
close all;
clc;
k=15; %导热系数,控制平滑
lambda=0.15; %控制平滑
N=20; %迭代次数
img=double(imread('lena.jpg'));
imshow(img,[]);
[m n]=size(img);
imgn=zeros(m,n);
for i=1:N
for p=2:m-1
for q=2:n-1
%当前像素的散度,对四个方向分别求偏导,局部不同方向上的变化量,
%如果变化较多,就证明是边界,想方法保留边界
NI=img(p-1,q)-img(p,q);
SI=img(p+1,q)-img(p,q);
EI=img(p,q-1)-img(p,q);
WI=img(p,q+1)-img(p,q);
%四个方向上的导热系数,该方向变化越大,求得的值越小,从而达到保留边界的目的
cN=exp(-NI^2/(k*k));
cS=exp(-SI^2/(k*k));
cE=exp(-EI^2/(k*k));
cW=exp(-WI^2/(k*k));
imgn(p,q)=img(p,q)+lambda*(cN*NI+cS*SI+cE*EI+cW*WI); %扩散后的新值
end
end
img=imgn; %整个图像扩散完毕,用已扩散图像的重新扩散。
end
figure;
imshow(imgn,[]);
![]()
matlab练习程序(TV模型图像修复)
曾经想要实现过Bertalmio图像修复算法,无奈自身实力不够,耗费两天时间也没能实现。昨天博客上有人问到TV模型,这个模型我过去是没听说过的,于是就找来相关论文研究了一下,发现TV模型也可以用来修复图像,于是就有了想实现的想法。用到的偏微分方程技巧和各项异性扩散很像。
先看看效果吧:
原lena:
随手截的噪声图:
合成的需要修复的图:
修复后的图(没有处理边界):
对于从来没有接触过图像修复的我来说,效果真是惊艳了。
下面介绍运算步骤:
和各项异性扩散类似,整个算法也是基于迭代的,迭代公式如下:
其中Io代表当前处理的像素,Ip代表邻域像素,p就可以取news四邻域。H定义如下:
这里的lambda为自定义的平滑系数。wp的定义如下:
这里a同样是自定义。
结合上图在看up散度,将p取e来看ue定义如下:
这里的h就是1了。
如此上述所有公式倒着运算不断迭代就可以了,迭代次数可自定义,或是不断迭代直到某条件成立都是可以的。
matlab代码如下,并不长,变量名和公式名是一一对应的:
![]()
close all;
clear all;
clc;
img=double(imread('lena.jpg'));
mask=rgb2gray(imread('ma.jpg'))>160;
[m n]=size(img);
for i=1:m
for j=1:n
if mask(i,j)==0
img(i,j)=0;
end
end
end
imshow(img,[]); %合成的需要修复的图像
lambda=0.2;
a=0.5;
imgn=img;
for l=1:300 %迭代次数
for i=2:m-1
for j=2:n-1
if mask(i,j)==0 %如果当前像素是被污染的像素,则进行处理
Un=sqrt((img(i,j)-img(i-1,j))^2+((img(i-1,j-1)-img(i-1,j+1))/2)^2);
Ue=sqrt((img(i,j)-img(i,j+1))^2+((img(i-1,j+1)-img(i+1,j+1))/2)^2);
Uw=sqrt((img(i,j)-img(i,j-1))^2+((img(i-1,j-1)-img(i+1,j-1))/2)^2);
Us=sqrt((img(i,j)-img(i+1,j))^2+((img(i+1,j-1)-img(i+1,j+1))/2)^2);
Wn=1/sqrt(Un^2+a^2);
We=1/sqrt(Ue^2+a^2);
Ww=1/sqrt(Uw^2+a^2);
Ws=1/sqrt(Us^2+a^2);
Hon=Wn/((Wn+We+Ww+Ws)+lambda);
Hoe=We/((Wn+We+Ww+Ws)+lambda);
How=Ww/((Wn+We+Ww+Ws)+lambda);
Hos=Ws/((Wn+We+Ww+Ws)+lambda);
Hoo=lambda/((Wn+We+Ww+Ws)+lambda);
imgn(i,j)=Hon*img(i-1,j)+Hoe*img(i,j+1)+How*img(i,j-1)+Hos*img(i+1,j)+Hoo*img(i,j);
end
end
end
img=imgn;
end
figure;
imshow(img,[])
![]()