【LeetCode】面试算法总结@树、二叉树、图

1、LeetCode----102. 二叉树的层次遍历

https://leetcode-cn.com/problems/binary-tree-level-order-traversal/submissions/

基本思路

#首先根据题解的含义，需要做的是对二叉树进行广度优先的遍历操作。
#但是，从题给的答案我们能看到，题目的要求是我们应该将二叉树的每一层内容分割开来。
#首先想到的广度优先遍历，但是每次遍历我们应该再设置一个队列一个装此层次的所有节点。
#另外一个队列装下一层次的所有节点，每次对每一层的所有节点进行遍历操作。
#遍历完一层之后，我们将下一层的节点复制到本层中再次进行迭代操作。
#外层的循环是一个死循环，想出去的话必须设置break语句
#考虑到节点遍历完成之后存储遍历值的数组是不会改变内容的，所以加入一个答案检验字段进行检验，当遍历一次之后答案数列没有更新则退出遍历。
#依次操作就完成了遍历过程，放回所需的答案。
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        queue = [root]
        next_que = []
        answer = []
        answer_now = []
        answer_tem = []
        if not root:
            return
        while 1:
            while queue:
                node = queue.pop(0)
                answer_tem.append(node.val)
                if node.left:
                    next_que.append(node.left)
                if node.right:
                    next_que.append(node.right)
            if answer_tem:
                answer.append(answer_tem)
            answer_tem = []
            queue = next_que.copy()
            next_que = []
            if answer_now == answer:
                break
            answer_now = answer.copy()
        return answer

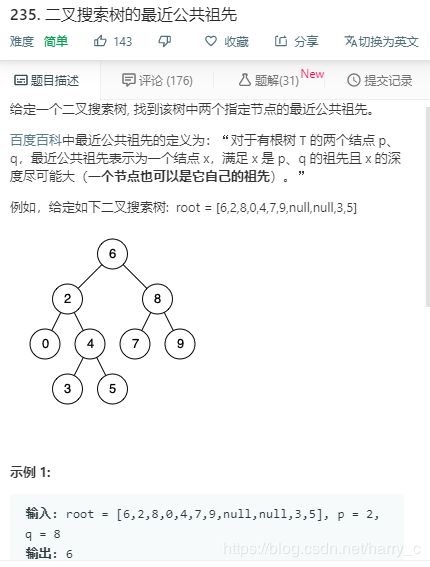
2、LeetCode----235. 二叉搜索树的最近公共祖先

https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/submissions/

基本思路

#首先考虑的是二叉搜索树的特性，右子树永远比根大，左子树永远比根小。
#我们通过其特点构建出逻辑，当pq的值都大于根的时候，公共节点肯定在左子树，反之在右子树。
#如果全大或者全小都不成立，我们能够立刻判断此时访问的节点就是共有根
#注意比较大小的时候没有等于号，要好好推敲。
class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        while root:
            if root.val > p.val and root.val > q.val and root.right:
                root = root.left
            elif root.val < p.val and root.val < q.val and root.left:
                root = root.right
            else:
                return root

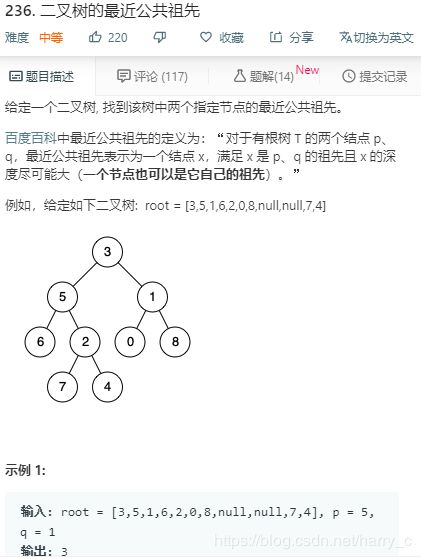
3、LeetCode----236. 二叉树的最近公共祖先

https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/submissions/

基本思路

#首先我们想好使用什么类型的算法，确定使用递归算法。
#通过查找左节点和右节点的方式，如果我们要查找的节点在左子树或者右子树的节点上找到的话，返回节点
#并且此节点不为空时也应该返回此节点以继续递归此节点。否则就返回空
#当一个节点的子树找到了p和q那么此节点为同根节点
#如果只找到了左子树，那么我们返回右子树继续递归
#如果只找到了右子树，那么我们返回左子树继续递归
#一直进行下去，知道找到左右子树返回我们的节点即为最终的共有祖先节点，否则返回空，无此节点。

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        return self.search_node(root, p, q)
    
    def search_node(self, root, p, q):
        if not root or root==p or root ==q:
            return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        if left and right:
            return root
        if not left:
            return right
        if not right:
            return left
        return None

4、LeetCode----104. 二叉树的最大深度

https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/submissions/

Solution1

#求二叉树的最大深度，首先想到的是深度优先遍历，构造深度优先遍历算法使用递归是很方便的。
#每次进行递归查找左右子树时我们记录一个level值，并且把当前的值与返回的lenel1和lenel2比较，取较大的一个。
#递归遍历，首先当为根节点时，访问左子树第一个节点，深度加1，再访问他的左子树，有则深度加一，没有则返回level
#访问完成所有的左根节点时，我们求解到的是左边的最大深度，进而访问右边的子树，最终返回左右子树中较大的作为最终的最大深度。
class Solution1:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        return self.compute(root, 0)
    
    def compute(self, root, level):
        if not root:
            return level
        level_1 = self.compute(root.left, level+1)
        level_2 = self.compute(root.right, level+1)
        if level_1 > level:
            level = level_1
        if level_2 > level:
            level = level_2
        return level

Solution2

#这也是使用递归的算法解决，但比较简洁，原理是一样的，每次都递归求出左右子树的最大深度，每次深度加1，（因为每次求左右子树时深度加了1）
#如此递归下去最终返回的是最大层数
#时间和空间复杂度和上面的代码是相当的
class Solution2:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

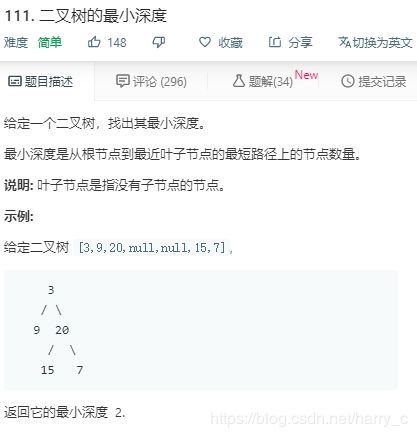
5、LeetCode----111. 二叉树的最小深度

https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/submissions/

基本思路

#与最大深度不同的是，我们应该判断是否为最小深度，我们只需判断此节点是否为叶子结点即可，如果是叶子结点，那么返回的深度为1加上上一次计算#的最小深度就是整棵树的最小深度值
#首先应该保证返回左子树和右子树的最小深度，在保证此条件的基础上我们还应该判断：
#如果没有右子树，我们则返回左子树的最小深度，如果没有左子树我们则返回右子树的最小深度
#如果没有左子树也没有右子树，那么此节点为我们要找的深度节点，返回1即可，无法将此1加上之前求得的上一次的最小深度则为本二叉树的最小深度
#如此递归下去求得最小叶子结点的层数。
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        if not root.left and not root.right:
            return 1
        if not root.left:
            return 1+self.minDepth(root.right)
        if not root.right:
            return 1+self.minDepth(root.left)
        return 1 + min(self.minDepth(root.left), self.minDepth(root.right))