CNN中FLOPs计算
转载地址:https://blog.csdn.net/sinat_34460960/article/details/84779219
在这之前我们先看一下CNN的前向传播计算公式,便于理解什么是parameters和FLOPs,这里参考Andrew老师课堂上的课件,如下:
前向传播过程其实就是将输入或上层输出左乘以一个W,然后加上一个b,最后使用合适的\sigma函数进行激活的过程,结果便是下层的输入或是最终的输出,多层网络就不断重复这个过程。
如果要让网络自己学习到输入数据中的良好特征,一般而言就需要搭建较复杂的网络,也就是包含更多的层,更大的层,更复杂的层等等。这基本是一个正相关的过程,即隐藏在数据中的特征越高层,网络就要越复杂,当然这个复杂是有一个合适的度的,不然就存在欠拟合和过拟合的问题了。
于是这就会产生一些实践上的问题,一是这个复杂的网络到底需要多少参数才能定义它?二是数据过一遍这么复杂的网络需要多大的计算量呢?这也分别就是我们今天要讨论的两个量:parameters和FLOPs。
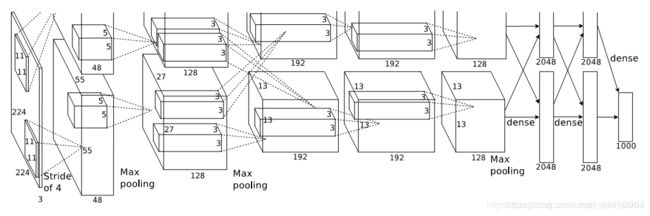
在本文中,我们以下图的AlexNet网络模型来说明在CNN中二者的计算过程:
-
parameters
从Andrew的前向传播PPT中,我们可以知道CNN中的parameters分为两种:W和b,注意这里W是大写,表示一个矩阵,也因此它相比b,既含有更多的信息,同时也是parameters的主要部分。
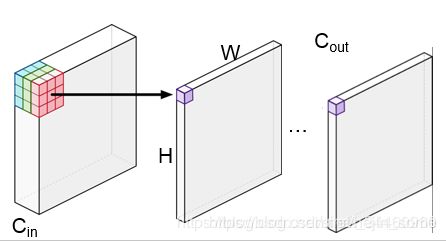
在AlexNet模型结构图中,每个大长方体中的小长方体就是W,它是大小为[K_h, K_w, C_{in}]的三维矩阵,其中K_h表示卷积核(filter或kernel)的高度,K_w表示卷积核的宽度,C_{in}表示输入的通道数(Channels),一般情况下,K_h和K_w的大小是一样的,且一般比较小,3、5、7之类。
同时由于CNN特点,我们知道,一个卷积核在输入数据上从左往右、从上往下扫一遍,便会计算出很多个前向传播的值,这些值就会按原来相对位置拼成一个feature map,当然一个卷积核提取的信息太过有限,于是我们需要N个不同的卷积核各扫数据,于是会产生N个feature map,这N个feature map在拼在一起就是这一层的输出,也是一个三维矩阵,即大长方体。设每个卷积核扫一遍之后输出的高度和宽度分别为H, W(注意区分两个W),同时N就是输出的通道数,记作C_{out},则输出矩阵大小为[H, W, C_{out}}]。
例如在从AlexNet图中左边第一个大长方体(输入图片)到第二个大长方体(图中是两个并列小长方体,这是作者分布式训练的需要,这里分析时可以将二者并起来看)这个过程,即是从[H, W, C_{in}] = [224, 224, 3]的矩阵,经过[K_h, K_w, C_{in}] = [11, 11, 3]的卷积核,变为[H, W, C_{out}] = [55, 55, 48+48]的矩阵的过程。
注意到两个特点,一是W是一个三维矩阵,通道数始终和输入数据保持一致,所以实际是二维空间的扫描,二是W在扫描的过程中是不变的,即一个卷积核是扫一遍数据而不是某个点。于是对于AlexNet模型的第一层卷积,W的大小是[K_h, K_w, C_{in}] = [11, 11, 3],个数是N,也就是C_{out} = 96,于是这一个卷积层的parameters中权重的个数为(K_h * K_w * C_{in}) * C_{out} = (11 * 11 * 3) * 96 = 34,848。
另外对于b,从前向传播公式可以看出,和W是一一对应的,维度也和W是对应的,即[C_{out}, ],还是对于AlexNet的第一个卷积层,parameters中偏置的个数为C_{out} = 96。
于是我们可以总结出规律:对于某一个卷积层,它的parameters个数为:(K_h * K_w * C_{in}) * C_{out} + C_{out},参数定义同上文。
刚才讲的都是对于卷积层的,对于全连接层,比如AlexNet的后三层,其实要更简单,因为这实际是两组一维数据之间(如果是卷积层过度到全连接层,如上图第5层到第6层,会先将第5层三维数据flatten为一维,注意元素总个数未变)的两两连接相乘,然后加上一个偏置即可。所以我们也可以总结出规律:对于某个全连接层,如果输入的数据有N_{in}个节点,输出的数据有N_{out}个节点,它的parameters个数为:N_{in} * N_{out} + N_{out}。如果上层是卷积层,N_{in}就是上层的输出三维矩阵元素个数,即三个维度相乘。
-
FLOPs
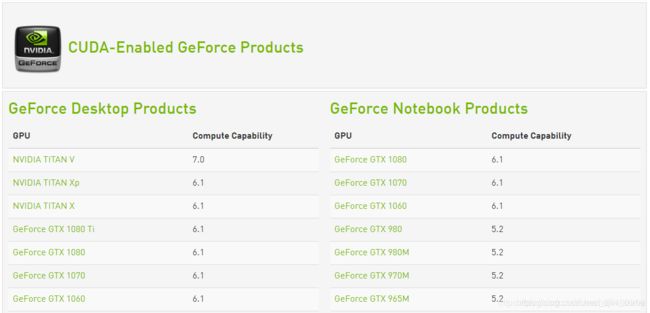
首先介绍一个很形似的概念——FLOPS:全称是floating point operations per second,意指每秒浮点运算次数,即用来衡量硬件的计算性能,比如nvidia官网上列举各个显卡的算力(Compute Capability)用的就是这个指标,如下图,不过图中是TeraFLOPS,前缀Tera表示量级:MM,2^12之意。
这里我们讨论的FLOPs全称是floating point operations,即表示浮点运算次数,小s后缀是复数的缩写,可以看做FLOPS在时间上的积分,区别类似速度和时间。
同样从Andrew的前向传播PPT中,我们也可以看到,这里的浮点运算主要就是W相关的乘法,以及b相关的加法,每一个W对应W中元素个数个乘法,每一个b对应一个加法,因此好像FLOPs个数和parameters是相同的。
但其实有一个地方我们忽略了,那就是每个feature map上每个点的权值是共享,这是CNN的一个重要特性,也可以说是优势(因此才获得特征不变性,以及大幅减少参数数量),所以我们在计算FLOPs是只需在parameters的基础上再乘以feature map的大小即可,即对于某个卷积层,它的FLOPs数量为:[(K_h * K_w * C_{in}) * C_{out} + C_{out}] * (H * W) = num\_params * (H * W),其中num\_params表示该层参数的数目。
还是里AlexNet网络第一卷积层为例,它的FLOPs数目为: [(11 * 11 * 3) * 96 + 96] * (55 * 55) = 105,705,600。
对于全连接层,由于不存在权值共享,它的FLOPs数目即是该层参数数目:N_{in} * N_{out} + N_{out}。
小结
运用上面的规律,我们便可以很轻松地计算出AlexNet网络的parameters和FLOPs数目,如下图(来自网络,出处已不可考):
这里不再重复举例。但是其中就是有一个地方和我算的有出入:第四卷积层的FLOPs数目,我计算是:1.3M * 13 * 13 = 219.7M,图中是112M。
最后还要说一点关于FLOPs的计算,在知乎上也有讨论,另外Nvidia的Pavlo Molchanov等人的文章的APPENDIX中也有介绍,由于是否考虑biases,以及是否一个MAC算两个operations等因素,最终的数字上也存在一些差异。但总的来说,计算FLOPs其实也是在对比之下才显示出某种算法,或者说网络的优势,如果我们坚持一种计算标准下的对比,那么就是可以参考的,有意义的计算结果。