PyTorch实现神经网络优化方法

1. 了解不同的优化方法

1.1 动量法（Momentum）

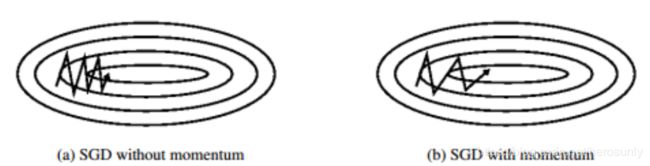
  该适用于隧道型曲面，梯度下降法在狭长的隧道型函数上表现不佳，如下图所示

• 函数主体缓缓向右方下降
• 在主体方向两侧各有一面高墙，导致垂直于主体方向有更大的梯
  度
• 梯度下降法会在隧道两侧频繁震荡

  而动量法每次更新都吸收一部分上次更新的余势。这样主体方向的更新就得到了更大的保留，从而效果被不断放大。物理上这就像是推一个很重的铁球下山，因为铁球保持了下山主体方向的动量，所以在隧道上沿两侧震荡测次数就会越来越少。
$$v_t=\gamma v_{t-1}+\eta {\nabla }_{\theta }J(\theta )$$
$${\theta }_t={\theta }_{t-1}-v_t$$

1.2 Adagrad

  该算法的特点是自动调整学习率，适用于稀疏数据。梯度下降法在每一步对每一个参数使用相同的学习率，这种一刀切的做法不能有效的利用每一个数据集自身的特点。
  Adagrad 是一种自动调整学习率的方法：

• 随着模型的训练，学习率自动衰减
• 对于更新频繁的参数，采取较小的学习率
• 对于更新不频繁的参数，采取较大的学习率

1.3 Adadelta(Adagrad的改进算法)

  Adagrad的一个问题在于随着训练的进行，学习率快速单调衰减。Adadelta则使用梯度平方的移动平均来取代全部历史平方和。
  定义移动平均：$E[g^2{]}_t=\gamma E[g^2{]}_{t-1}+(1-\gamma )g_t^2$
  Adadelta 的第一个版本也叫做 RMSprop，是Geoff Hinton独立于Adadelta提出来的。

1.4 Adam

  如果把Adadelta里面梯度的平方和看成是梯度的二阶矩，那么梯度本身的求和就是一阶矩。Adam算法在Adadelta的二次矩基础之上又引入了一阶矩。而一阶矩，其实就类似于动量法里面的动量。

1.5 如何选择算法

• 动量法与Nesterov的改进方法着重解决目标函数图像崎岖的问题
• Adagrad与Adadelta主要解决学习率更新的问题
• Adam集中了前述两种做法的主要优点
• 目前为止 Adam 可能是几种算法中综合表现最好的

2. 代码实践

2.1 导入数据

import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt

torch.manual_seed(1)    # reproducible

LR = 0.01
BATCH_SIZE = 32
EPOCH = 12

# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))

# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()

torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)

2.2 构建神经网络和优化器

# 默认的 network 形式
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(1, 20)   # hidden layer
        self.predict = torch.nn.Linear(20, 1)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

# 为每个优化器创建一个 net
net_SGD         = Net()
net_Momentum    = Net()
net_RMSprop     = Net()
net_Adam        = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]

# different optimizers
opt_SGD         = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum    = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop     = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam        = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]

loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []]   # 记录 training 时不同神经网络的 loss

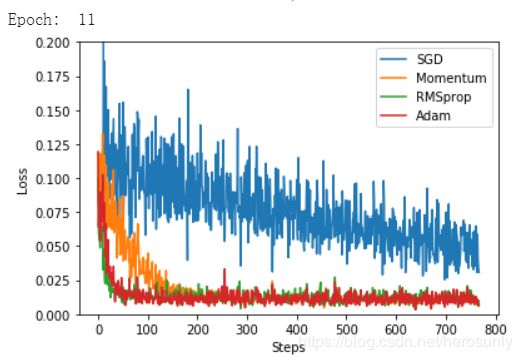
2.3 训练并绘制结果

for epoch in range(EPOCH):
    print('Epoch: ', epoch)
    for step, (b_x, b_y) in enumerate(loader):          # for each training step
        for net, opt, l_his in zip(nets, optimizers, losses_his):
            output = net(b_x)              # get output for every net
            loss = loss_func(output, b_y)  # compute loss for every net
            opt.zero_grad()                # clear gradients for next train
            loss.backward()                # backpropagation, compute gradients
            opt.step()                     # apply gradients
            l_his.append(loss.data.numpy())     # loss recoder

    labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
    for i, l_his in enumerate(losses_his):
        plt.plot(l_his, label=labels[i])
    plt.legend(loc='best')
    plt.xlabel('Steps')
    plt.ylabel('Loss')
    plt.ylim((0, 0.2))
    plt.show()