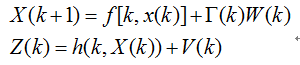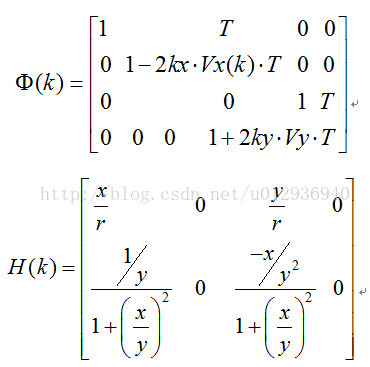扩展卡尔曼滤波原理
转自:https://blog.csdn.net/u012936940/article/details/77249245/
参考自:http://home.wlu.edu/~levys/kalman_tutorial/
https://github.com/simondlevy/SensorFusion
1、理论部分
上一篇介绍了线性卡尔曼滤波器,当系统为线性高斯模型时,滤波器能给出最优的估计,但是实际系统总是存在不同程度的非线性,如平方、三角关系、开方等。对于非线性系统,可以采用的一种方法是通过线性化方法将非线性系统转换为近似的线性系统,即为EKF,核心思想是:围绕滤波值将非线性函数展开成泰勒级数并略去二阶及以上项,得到一个近似的线性化模型,然后应用卡尔曼滤波完成状态估计。
系统方程
各个变量意义同上一节,其中f和h代表状态和观测的非线性函数。
在扩展卡尔曼滤波中,状态的预测以及观测值的预测由非线性函数计算得出,线性卡尔曼滤波中的状态转移矩阵A阵和观测矩阵H阵由f和h函数的雅克比矩阵代替,假设状态有n维,则求法如下:
有了上面矩阵的计算方法,EKF滤波过程同线性卡尔曼滤波相同,公式如下
2、实践部分
根据图中情景,选取横向位置、速度,纵向位置、速度为状态量,列出下面非线性状态方程及观测方程
根据状态方程和观测方程,计算雅克比矩阵如下
close all;
clear all;
%% 真实轨迹模拟
kx = .01; ky = .05; % 阻尼系数
g = 9.8; % 重力
t = 15; % 仿真时间
Ts = 0.1; % 采样周期
len = fix(t/Ts); % 仿真步数
dax = 3; day = 3; % 系统噪声
X = zeros(len,4);
X(1,:) = [0, 50, 500, 0]; % 状态模拟的初值
for k=2:len
x = X(k-1,1); vx = X(k-1,2); y = X(k-1,3); vy = X(k-1,4);
x = x + vx*Ts;
vx = vx + (-kx*vx^2+dax*randn(1,1))*Ts;
y = y + vy*Ts;
vy = vy + (ky*vy^2-g+day*randn(1))*Ts;
X(k,:) = [x, vx, y, vy];
end
%% 构造量测量
dr = 8; dafa = 0.1; % 量测噪声
for k=1:len
r = sqrt(X(k,1)^2+X(k,3)^2) + dr*randn(1,1);
a = atan(X(k,1)/X(k,3))*57.3 + dafa*randn(1,1);
Z(k,:) = [r, a];
end
%% ekf 滤波
Qk = diag([0; dax/10; 0; day/10])^2;
Rk = diag([dr; dafa])^2;
Pk = 10*eye(4);
Pkk_1 = 10*eye(4);
x_hat = [0,40,400,0]';
X_est = zeros(len,4);
x_forecast = zeros(4,1);
z = zeros(4,1);
for k=1:len
% 1 状态预测
x1 = x_hat(1) + x_hat(2)*Ts;
vx1 = x_hat(2) + (-kx*x_hat(2)^2)*Ts;
y1 = x_hat(3) + x_hat(4)*Ts;
vy1 = x_hat(4) + (ky*x_hat(4)^2-g)*Ts;
x_forecast = [x1; vx1; y1; vy1]; %预测值
% 2 观测预测
r = sqrt(x1*x1+y1*y1);
alpha = atan(x1/y1)*57.3;
y_yuce = [r,alpha]';
% 状态矩阵
vx = x_forecast(2); vy = x_forecast(4);
F = zeros(4,4);
F(1,1) = 1; F(1,2) = Ts;
F(2,2) = 1-2*kx*vx*Ts;
F(3,3) = 1; F(3,4) = Ts;
F(4,4) = 1+2*ky*vy*Ts;
Pkk_1 = F*Pk*F'+Qk;
% 观测矩阵
x = x_forecast(1); y = x_forecast(3);
H = zeros(2,4);
r = sqrt(x^2+y^2); xy2 = 1+(x/y)^2;
H(1,1) = x/r; H(1,3) = y/r;
H(2,1) = (1/y)/xy2; H(2,3) = (-x/y^2)/xy2;
Kk = Pkk_1*H'*(H*Pkk_1*H'+Rk)^-1; %计算增益
x_hat = x_forecast+Kk*(Z(k,:)'-y_yuce); %校正
Pk = (eye(4)-Kk*H)*Pkk_1;
X_est(k,:) = x_hat;
end
%%
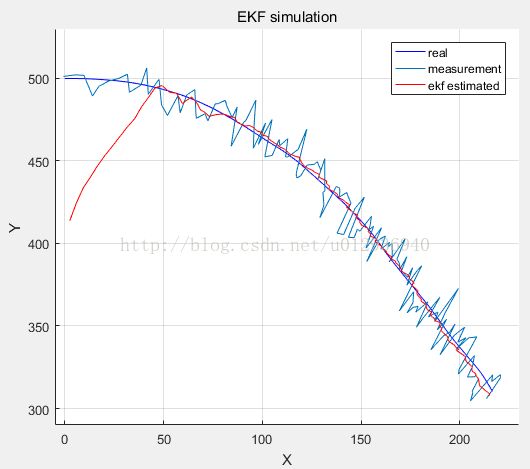
figure, hold on, grid on;
plot(X(:,1),X(:,3),'-b');
plot(Z(:,1).*sin(Z(:,2)*pi/180), Z(:,1).*cos(Z(:,2)*pi/180));
plot(X_est(:,1),X_est(:,3), 'r');
xlabel('X');
ylabel('Y');
title('EKF simulation');
legend('real', 'measurement', 'ekf estimated');
axis([-5,230,290,530]);