NLP Task5

学习内容

朴素贝叶斯
朴素贝叶斯的原理
利用朴素贝叶斯模型进行文本分类

SVM模型
SVM的原理
利用SVM模型进行文本分类

LDA主题模型
pLSA、共轭先验分布
LDA
使用LDA生成主题特征，在之前特征的基础上加入主题特征进行文本分类
LDA数学八卦

朴素贝叶斯

贝叶斯定理

讲朴素贝叶斯之前，先普及一个概率论的小知识点，贝叶斯定理，这个定理也是朴素贝叶斯算法的基础。即
$$P(Y|X)=\frac{P(XY)}{P(X)}=\frac{P(X|Y)P(Y)}{P(X)}$$
因为实际生活中经常遇到这种情况：我们可以很容易直接得出P(X|Y)，P(Y|X)则很难直接得出，但我们更关心P(Y|X)，贝叶斯定理就为我们打通从P(X|Y)获得P(Y|X)的道路。比如Y表示待预测变量，X表示数据的特征，通常情况我们需要根据特征X预测结果Y，所以通过该定理就可以由数据得出预测模型。

朴素贝叶斯分类器

SVM模型

LDA主题模型

pLSA

pLSA主要是改进了LSA模型，在LSA模型在概率层次的拓展，是一种主题模型。LSA是类似SVD在推荐系统中的应用，其使用在文档的表示上面，通过文档中词汇的频数或权重，将其进行矩阵分解，达到降维的目的。
pLSA的原理图如下：

主要的思想是通过引入中间变量Z（主题），来进行建模，算法的流程如下：

通过数据可以得到P(d,w),需要求取P(w|d)则需要对P(z|d)和P(w|z)进行求解。对概率函数求取最大似然可得：

其中，为n（dm,wn）表示文档-单词对出现的次数。为加以区分，之后上标进行修改M’,N’，使用与标识对应文档与词汇数量。

下面就是根据EM算法来进行迭代求解，主要分为E步和M步， 基本实现思想是：
(1)E步骤：求隐含变量Given当前估计的参数条件下的后验概率。
(2)M步骤：最大化Complete data对数似然函数的期望，此时我们使用E步骤里计算的隐含变量的后验概率，得到新的参数值。
两步迭代进行直到收敛。
E步求解隐变量的后验概率:

M步求解该最大似然：

最后可得下式进行迭代循环：


通过M步求得的条件概率，带回E步进行迭代循环。

共轭先验分布

    因为在贝叶斯中有一个规律：先验+最大似然=后验，如果使得先验和后验的分布相同的话，如果后验概率和先验概率满足同样的分布律（同分布），那么，先验分布叫作似然函数的共轭先验分布，先验分布和后验分布被叫作共轭分布。共轭先验的好处主要在于代数上的方便性，可以直接给出后验分布的封闭形式，否则的话只能数值计算。同时从先验到后验的变化过程中从数据补充到的物理知识，也有助于物理解释。

LDA原理

许多背景知识就不详细介绍了，一些数据的相关理论背景可以参考，《LDA数学八卦》和《LDA漫游指南》，这两本的在理论上面介绍的非常详细了。
主要将pLSA和LDA进行对比理解：

首先，我们来看看PLSA和LDA生成文档的方式。在PLSA中，生成文档的方式如下：

1. 按照概率$p(d_i)$选择一篇文档$d_i$
2. 根据选择的文档$d_i$，从从主题分布中按照概率$p({\zeta }_k\mid d_i)$选择一个隐含的主题类别${\zeta }_k$.
3. 根据选择的主题${\zeta }_k$, 从词分布中按照概率$p({\omega }_j\mid {\zeta }_k)$选择一个词${\omega }_j$.

LDA 中，生成文档的过程如下：

1. 按照先验概率$p(d_i)$选择一篇文档$d_i$
2. 从Dirichlet分布$\alpha$中取样生成文档$d_i$的主题分布${\theta }_i$，主题分布${\theta }_i$由超参数为$\alpha$的Dirichlet分布生成
3. 从主题的多项式分布${\theta }_i$中取样生成文档$d_i$第 j 个词的主题$z_{i,j}$
4. 从Dirichlet分布$\beta$中取样生成主题$z_{i,j}$对应的词语分布${\varphi }_{z_{i,j}}$，词语分布${\varphi }_{z_{i,j}}$由参数为$\beta$的Dirichlet分布生成
5. 从词语的多项式分布${\varphi }_{z_{i,j}}$中采样最终生成词语${\omega }_{i,j}$

pLSA原理图：

LDA原理图：

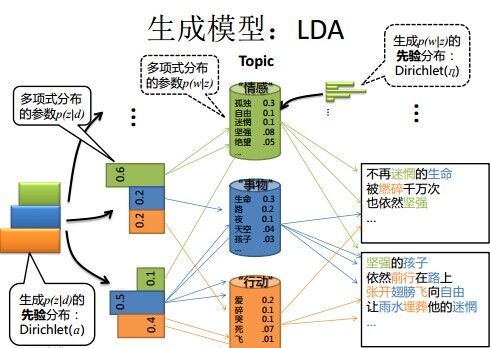
LDA的求解方法一般有两种：第一种是基于Gibbs采样算法求解，第二种是基于变分推断EM算法求解。

代码范例

import tensorflow as tf
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import roc_auc_score
from sklearn.metrics import auc
from sklearn.metrics import f1_score,precision_score,recall_score
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
import lda

#导入sklearn自带的文本分类包，包括20个类别
newsgroups_train = fetch_20newsgroups(subset='train')
from pprint import pprint
pprint(list(newsgroups_train.target_names))

#进取我4个类别作为文本分类样例，并根据词频来进行特征矩阵构建（LDA需要词频矩阵）
categories = ['alt.atheism', 'talk.religion.misc',
              'comp.graphics', 'sci.space']
newsgroups_train = fetch_20newsgroups(subset='train',
                                      categories=categories)
vectorizer = CountVectorizer()
vectors = vectorizer.fit_transform(newsgroups_train.data)
vectors.shape
#训练贝叶斯模型，并计算F1值
newsgroups_test = fetch_20newsgroups(subset='test',
                                     categories=categories)
vectors_test = vectorizer.transform(newsgroups_test.data)
clf = MultinomialNB(alpha=.01)
clf.fit(vectors, newsgroups_train.target)
pred = clf.predict(vectors_test)
metrics.f1_score(newsgroups_test.target, pred, average='macro')
#训练SVM模型并计算F1值
clf = SVC(kernel='linear')
clf.fit(vectors, newsgroups_train.target)
pred = clf.predict(vectors_test)
metrics.f1_score(newsgroups_test.target, pred, average='macro')
#训练LDA模型，并进行数据特征转换，讲主题特征加入原来数据
model = lda.LDA(random_state=1, n_topics=20, n_iter=1000)
model.fit(vectors)
lda_vectors = model.transform(vectors)
lda_vectors_test = model.transform(vectors_test)
#再次模型并计算，F1值
#贝叶斯
newsgroups_test = fetch_20newsgroups(subset='test',
                                     categories=categories)
vectors_test = vectorizer.transform(newsgroups_test.data)
clf = MultinomialNB(alpha=.01)
vectors_add_lda = np.hstack((vectors.toarray(),lda_vectors))
clf.fit(vectors_add_lda, newsgroups_train.target)
vectors_test_add_lad = np.hstack((vectors_test.toarray(),lda_vectors_test))
pred = clf.predict(vectors_test_add_lad)
metrics.f1_score(newsgroups_test.target, pred, average='macro')
#SVM
clf = SVC(kernel='linear')
vectors_add_lda = np.hstack((vectors.toarray(),lda_vectors))
clf.fit(vectors_add_lda, newsgroups_train.target)
vectors_test_add_lad = np.hstack((vectors_test.toarray(),lda_vectors_test))
pred = clf.predict(vectors_test_add_lad)
metrics.f1_score(newsgroups_test.target, pred, average='macro')

结论

最后发现加入LDA后对结果的影响不大，因为本来数据中特征数量大，大于1W，但是训练的主题仅选择20，维度远小于原数据，所以对结果影响不大，样例仅提供参考方法，实际使用的时候，要根据实际情况来进行处理。

参考资料

统计学习方法
https://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html
https://blog.csdn.net/hongyesuifeng/article/details/79674163
https://blog.csdn.net/u013710265/article/details/73480332
https://blog.csdn.net/KIDGIN7439/article/details/69831490
https://blog.csdn.net/puqutogether/article/details/43309717
https://blog.csdn.net/m0_37788308/article/details/78935021
https://blog.csdn.net/fengzhizi76506/article/details/79639585
https://blog.csdn.net/TiffanyRabbit/article/details/76445909