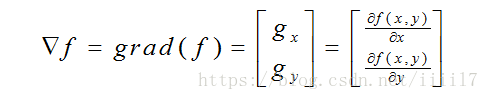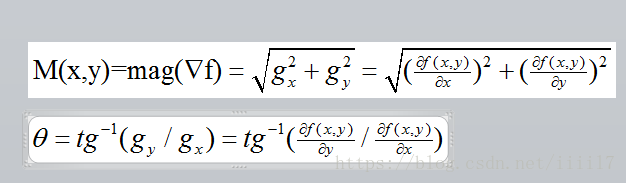（四）图像的空域锐化_一阶梯度算子

一，实验原理

图像锐化：增强图像的边缘或轮廓。

图像平滑通过积分过程使得图像边缘模糊，图像锐化则通过微分而使图像边缘突出、清晰。

梯度锐化法：

图像处理中应用微分最常用的方法是计算梯度。对于图像f(x，y)，在点(x，y)处的梯度定义为：

梯度是一个向量，其大小和方向为

离散图像处理时，常用到梯度的大小，因此习惯称梯度的大小为“梯度”。并且一阶偏导数采用一阶差分近似表示，即 

gx=f(x+1,y)-f(x,y)  

 gy=f(x,y +1)-f(x,y)

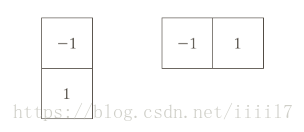
对应的模板为

为简化梯度的计算，经常使用

           grad( f )=Max(|gx|, |gy|)

  或   grad( f ）=|gx|+|gy|

除梯度算子以外，还可采用Roberts、Prewitt和Sobel算子计算梯度，来增强边缘。

Roberts算子：

    gx =f(x+1,y+1)-f(x,y) 

    gy =f(x+1,y)-f(x,y+1)

对应的模板

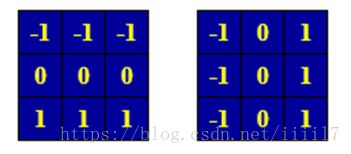
Prewitt算子:

    gx =f(x+1,y-1)-f(x-1,y-1)​​​​​​​+f(x+1,y) -f(x-1,y)+f(x+1,y+1)-f(x-1,y+1)

    gy =f(x-1,y+1)-f(x-1,y-1)​​​​​​​+f(x,y+1) -f(x,y-1)+f(x+1,y+1)-f(x+1,y-1)

对应的模板为：

Sobel算子：

    gx =f(x+1,y-1)-f(x-1,y-1)​​​​​​​+2f(x+1,y) -2f(x-1,y)+f(x+1,y+1)-f(x-1,y+1)

    gy =f(x-1,y+1)-f(x-1,y-1)​​​​​​​+2f(x,y+1) -2f(x,y-1)+f(x+1,y+1)-f(x+1,y-1)

二，实验代码和结果

%原图 Roberts边缘检测 Prewitt边缘检测 Sobel边缘检测
clc;
clear;
close all;

I=imread('test4.gif','gif');        %自己设置路径
subplot(2,2,1);
imshow(I);
title('test4原始图像');
G1=edge(I,'Roberts');
subplot(2,2,2);	
imshow(G1,[]);
title('test4Roberts边缘检测');
G2=edge(I,'Prewitt');
subplot(2,2,3);
imshow(G2,[]);
title('test4Prewitt边缘检测');
G3=edge(I,'Sobel');
subplot(2,2,4);
imshow(G3,[]);
title('test4Sobel边缘检测');

三，实验总结

一阶微分算子能有效提取图像边缘，但如果是整幅图片使用一阶微分算子提取，增强的图像仅显示灰度变化比较徒的边缘轮廓，而灰度变化比较平缓或均匀的区域则呈黑色。

附上实验原图