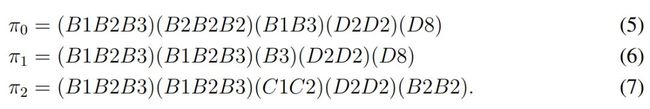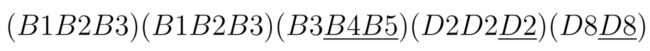一篇AI打麻将的论文，理科生眼中的麻将是这样的

额……报道了下围棋、打德州扑克的 AI 程序之后，小编终于看到了 AI 打麻将的一篇研究，两位作者分别来自悉尼科技大学和陕西师范大学。不过，自信麻将技术不错的小编翻译地一脸懵逼。本文强行为大家介绍了这篇 AI 麻将论文，感兴趣的同学可以查看原英文文章。

从 AI 研究的早期阶段，游戏就开始充当许多 AI 技术和想法的试验台，从跳棋、国际象棋、围棋、扑克到星际争霸 II。在过去的几十年里，AI 程序已经在跳棋、国际象棋、围棋等完整信息游戏中接连打败最优秀的人类棋手。在这些游戏中，玩家在做出决策之前可以知道所有信息。相比较而言，非完整信息游戏更加具有挑战性。最近，AI 在两人对决有限制和无限制德州扑克游戏中都取得了重要进展，这是人类在竞争中玩的最小的扑克变体。在本文中，研究者对更流行、更复杂的麻将游戏展开了数学和 AI 研究。

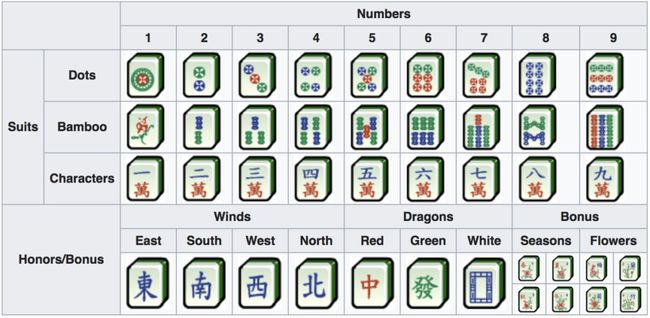
麻将是一种风靡全世界的多人对抗游戏。一套麻将有 144 张牌，牌面上有汉字或符号（见图 1），其出牌规则、得分灵活多变。开始的时候，每个玩家都有 13 张牌。接下来，他们会摸牌、出牌，直到攒够 14 张可以胡的牌型。

在这篇论文中，研究者对麻将进行数学和 AI 方面的研究，尝试回答两个最基本的问题：当前 14 张牌的牌面到底有多好；我们该打出哪一张牌？作者定义了缺牌数的概念，并提出最优策略来确定当前该打的牌，以在 k 次牌面变换（k ≥ 1）的条件下增加胡牌的概率。

在此论文中，为了简化问题，我们只考虑麻将最基础的打法 Mahjong-0。其他的打法可以用类推的方式处理。在 Mahjong-0 打法中，只有三类牌：

• 条：从 B1 至 B9 表示一条到九条，每类 4 张；

• 万：从 C1 至 C9 表示一万到九万，每类 4 张；

• 筒：从 D1 至 D9 表示一筒到九筒，每类 4 张。

此论文把牌面称为条（B）、万（C）、筒（D），把整副麻将记为 M_0，总共 108 张。

麻将规则

定义 1：将牌（eye）指一对同样的牌，碰（杠）指三张或者四张同样的牌。吃（chow）指同类牌组成连续的三张牌。杠子、刻子或者顺子都称之为组（meld）。

在此论文中，作者也给出了一些非标准概念。

定义 2：待吃（pseudochow，缩写为 pchow）是指一对同花色的牌，吃了一张牌之后能够成为一组顺子。待组（pseudomeld，缩写为 pmeld）是指一个待吃或者对。牌 c 能够和 ab 组成一组，就是一摊（abc）。类似的，一张牌 t 加上另一张 t 就是一将。

例如，B3B4B5 就是吃，C1C1 是将，B7B7B7 是碰，D9D9D9D9 是杠，B1B3 和 C2C3 都可以吃。

论文的第二部分介绍了很多形式化的麻将规则，包括什么是清一色，怎么样才算完整的牌面（胡牌）等等。例如定义 4 展示了 14 张牌的标准形式，其中作者将条（B）、万（C）、筒（D）表示为 0、1、2，因此 (0, 3) 就表示 B3：三条。

定义牌面的组合后，我们需要一种度量方法以确定到底当前 14 张牌离胡牌还有多远，这里作者引入了缺牌数（deficiency）。简单而言，缺牌数表示的就是当前牌面到胡牌还差多少张牌。

理科生怎样看待牌面？

如果我们定义了随机 14 张牌的牌面表示和缺牌数，现在只需要知道怎样评估当前牌面的好坏，并通过打牌来把缺牌数降低到 0 就行了。首先对于清一色的 14 张牌，它的缺牌数少于等于 3 张，论文的第三章主要就在讨论和证明这一点。

如下对于清一色的牌，只有在以下情况才会令缺牌数为 3：

对于常规牌，最大的缺牌数为 6，论文的第四章主要就在讨论和证明这一点。

现在根据缺牌数的定义与证明，我们就能度量当前牌面的好坏。我们首先需要定义根据缺牌完善后的完整牌面，然后计算缺牌和胡牌之间的成本。

这里我们可以举个栗子，如果我们摸上来的 14 张牌为：T = (B1B1B2B2B2B2B3B3)(C1C2C8)(D2D2D8)，其中 C2 表示二万。那么现在 p-decompositions 可以表示为：

π_0 中的 (B1 B3) 并不能组成顺，因为π_0 中已经有 4 张 B2 了。π_1 和 π_2 都是饱和与可被组合完全的，例如π_1 缺少的牌为：

它的成本 cost (π_1) = 4。确定最优成本后我们就需要寻找最优策略，并尽可能在最小的轮数下将成本或缺牌数降低为 0。当然，如果需要对打牌的过程建模，并找到最优策略，我们还需要更多的研究。

结语与讨论

在此论文中，作者开启了对麻将的数学和 AI 研究。在设计玩麻将的计算机程序时，本文先描述了缺牌数的定义，知识库的概念和步骤 k 值扮演者重要角色。

尽管麻将是个非常流行的棋牌游戏，但少有专门研究麻将的数学或者 AI 论文。据我们所知，Yuan Cheng 等人的论文 [4] 是首个使用数学技术（主要是基本组合理论）严肃研究麻将的论文。在那篇论文中，作者们研究了麻将中一组特殊的组合问题，也就是 k-gate 问题。

清一色的 13 张牌 T 可以称为 nine-gate，其中我们可以向 T 中添加任意同类牌而胡牌。对于 1 ≤ k ≤ 9，如果存在不同值的 K 张牌，且只能由这 k 张牌补全 T，那么 T 就可以称为 k-gate 问题。很容易看出，k-gate 问题能通过这篇论文构建的形式化表达进行描述。为了找到所有的 k-gate，我们只需要为每一个清一色的 13 张牌做决策，而不需要管是否正好有 k 张牌使得 T 加上 i 就能补全。

至少有三个可以扩展上述研究的方向。首先，我们可以在 M_0 中囊括更多牌，例如，东南西北这些风牌，红中、发财、白板这些箭牌，以及花牌。其次，我们可以增加或者减少 14 张手牌的规定，例如可以允许任意 7 对，或者要求至少两个花色。第三，不同的 14 张牌可以有不同的得分，例如，清一色比杂牌得分多。未来研究可以尝试解决这些问题。

论文：Let's Play Mahjong!

    论文地址：https://arxiv.org/pdf/1903.03294.pdf

作者：Sanjiang Li、Xueqing Yan

来源:arXiv, 机器之心

∞∞∞∞∞

公众号回复“IT派”，

邀你加入 IT派 { 深广创投圈 }