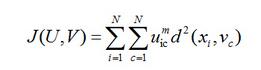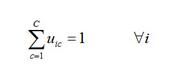FCM 算法

一 FCM算法概述

 FCM算法的全称是模糊C均值聚类算法，和K-means算法同属于聚类算法，但却有着本质的区别，就其命名而言，模糊二字无疑是该算法的重点，下面就先简单介绍一下：

1. 隶属度和模糊集

   　　隶属度函数用来描述元素x属于一个集合B的程度，假定为UB(x)，其中x为B中的任意元素，UB(x)的取值范围为[0,1]。在隶属度函数的基础上，称空间上X={x}上的隶属度函数为一个模糊集合。

2. 模糊聚类分析

   　　传统的聚类分析是把每个元素严格的划分到一个类中，属于硬划分。模糊聚类分析将聚类生成的每个簇均看做模糊集合，通过隶属度来确定聚类关系，是一种柔性划分，得到元素属于各个簇的不确定性程度，使得聚类结果更加准确灵活，因此，模糊聚类分析逐渐成为聚类分析的主流。

3.FCM

FCM算法是将N个L维向量分为C个模糊组，通过迭代不断更新隶属度以及聚类中心，最小化目标函数对数据进行聚类。

其中，目标函数为：

约束条件为：

根据隶属度的非负性，有

这里，m指的是模糊加权系数，它的值大于1；d(xi,vc)表示的是第i个数据点与第c个聚类中心的欧式距离；uic是隶属度矩阵中的元素，且[0,1]；vc是对应于每个聚类的聚类中心。

为了求含有约束条件的目标函数的极值，引入拉格朗日因子构造新的目标函数：

对于目标函数求极值的最优化条件如下：

从而得到隶属度和聚类中心的计算公式为：

根据上述公式不断迭代求出满足条件的隶属度以及聚类中心。具体的FCM算法步骤如下：

首先，给定一个由N个L维向量组成的数据集X以及所要分得的类别个数C，自定义隶属度矩阵

（1）设定类别的个数C和模糊系数m；

（2）‚初始化隶属度矩阵且满足公式（2）中的归一化条件；

（3）根据公式（5）计算聚类中心；

（4）根据公式（4）更新隶属度矩阵；

（5）根据矩阵范数比较迭代的隶属度矩阵，如果，迭代停止，否则返回（3）。

二 MATLAB实现

根据上述公式及步骤，采用MATLAB实现，具体如下：

（1）选取UCI数据库中的wine数据实现，代码：

clear all
clc;
%% 导入数据
load wine.txt;
cluster_n=6;

data = wine;
data(:,1) = [];
data(:,size(data,2)) = [];
data_n = size(data, 1); %数据的个数 
in_n = size(data, 2);% 数据维数

%% 定义变量
default_options = [10;    % 隶属度函数的幂次方
        300;    % 最大迭代次数
        1e-5;    %步长
        1];    % 判定条件

options = default_options;
expo = options(1);        % Exponent for U 隶属度函数的幂次方
max_iter = options(2);        % Max. iteration 最大迭代次数
min_impro = options(3);        % Min. improvement  最小进化步长
display = options(4);        % Display info or not 显示信息与否
obj_fcn = zeros(max_iter, 1);    % Array for objective function

tic
%% 初始化隶属度矩阵并归一
U = rand(cluster_n, data_n); %rand()产生随机矩阵 
col_sum = sum(U);
U = U./col_sum(ones(cluster_n, 1), :);%归一化

%% 开始迭代
for i = 1:max_iter,%迭代次数控制
    tic
    mf = U.^expo;      % MF matrix after exponential modification
    center = mf*data./((ones(size(data, 2), 1)*sum((mf')))'); % 建立新的聚类中心

       out = zeros(size(center, 1), size(data, 1));  %每个点到每个中心的距离，行数为中心数

        if size(center, 2) > 1,%样本的维数大于一执行以下程序
            for k = 1:size(center, 1),%给K赋值
                abc = ((data-ones(size(data,1),1) * center(k,:)).^2)';
                  out(k, :) = sqrt(sum(abc));%得到欧氏距离
            end
       else    % 1-D data
            for k = 1:size(center, 1),
                  out(k, :) = abs(center(k)-data)';
            end
        end

    obj_fcn(i) = sum(sum((out.^2).*mf));  % 目标函数
    tmp = out.^(-2/(expo-1));      % 根据新的隶属度矩阵求解公式求出
    U= tmp./(ones(cluster_n, 1)*sum(tmp));  % 新的隶属度矩阵

    if display, 
        fprintf('Iteration count = %d, obj. fcn = %f\n', i, obj_fcn(i));
        %输出迭代次数和函数的结果
    end
    % check termination condition
    if i > 1,  %进化步长控制
        if abs(obj_fcn(i) - obj_fcn(i-1)) < min_impro, break; end,
    end
    toc
end
toc

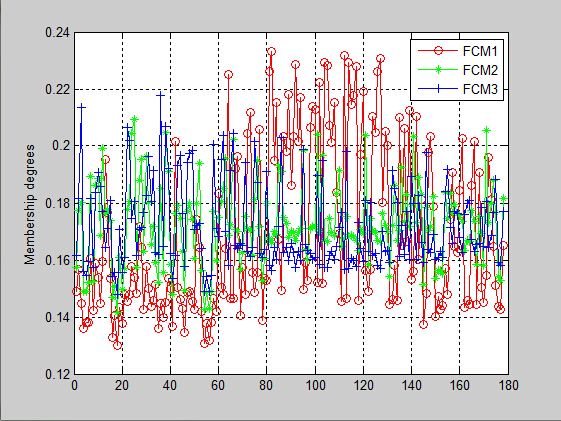
plot(U(1,:),'-ro');
grid on
hold on
plot(U(2,:),'-g*');
plot(U(3,:),'-b+');

ylabel('Membership degrees')
legend('FCM1','FCM2','FCM3','location','northeast');

toc

结果如下：

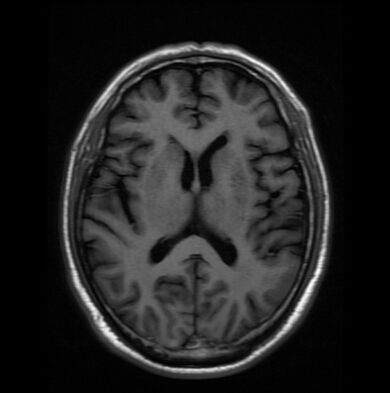
（2）选取一张MRI图像，进行图像分割，代码如下：

clear all 
clc;

a=imread('MRI.jpg');
I=imnoise(a,'salt & pepper',0.05);
figure(1);           
 imshow(I);title('加噪图像');

[height,width,c]=size(a);
if c~=1
    a=rgb2gray(a);
end

a=double(a);
[row,column]=size(a); 
data = a(:);
data_n = size(data,1);

cluster_num = 4;
default_options = [2.0;    % 隶属度函数的幂次方
        300;    % 最大迭代次数
        1e-5;    %步长
        1];    % 判定条件

options = default_options;


expo = options(1);        % Exponent for U 隶属度函数的幂次方
max_iter = options(2);        % Max. iteration 最大迭代次数
min_impro = options(3);        % Min. improvement  最小进化步长
display = options(4);        % Display info or not 显示信息与否

obj_fcn = zeros(max_iter, 1);    % Array for objective function
membership = zeros(height,width,cluster_num);
center = zeros(cluster_num,1);

tic
% 初始化隶属度并归一
for i=1:height 
    for j=1:width
        member_sum=0;
        for k=1:cluster_num
            membership(i,j,k)=rand();
            member_sum = member_sum + membership(i,j,k);
        end        
        for p =1:cluster_num
            membership(i,j,p) = membership(i,j,p) / member_sum;
        end
    end
end

tic
for i = 1:max_iter,%迭代次数控制
    mf = membership.^expo;     
    %%%%%%%%建立聚类中心
    for m = 1:cluster_num
        to = 0;
        tp =0;
        for j = 1:height
            for t = 1:width
                to = to + membership(j,t,m) * a(j,t);
                tp = tp + membership(j,t,m);
            end
        end
        center(m,1) = to / tp; 
    end

    %%%%%%%得到欧式距离以及目标函数
    out = zeros(height,width,cluster_num);
    for m =1:height
        for j =1:width
            for t = 1:cluster_num
                out(m,j,t) = abs(a(m,j) - center(t,1));
                obj_fcn(i) = obj_fcn(i) + (membership(m,j,t).^expo) * (out(m,j,t).^2);
            end
        end
    end

    for m = 1:height
        for j = 1:width
            for r = 1:cluster_num
                top =0;
                for t = 1:cluster_num
                    top = top + (out(m,j,r) / out(m,j,t)).^(expo - 1);
                end
                membership(m,j,r) = 1 / top;
            end
        end
    end

    %%%%%%归一化隶属度
    for m=1:height 
        for j = 1:width
            member_sum = 0;
            for k = 1:cluster_num
                member_sum = member_sum + membership(m,j,k);
            end
            for p = 1:cluster_num
                membership(m,j,p) = membership(m,j,p) / member_sum;
            end
        end
    end

     if display, 
        fprintf('Iteration count = %d, obj. fcn = %f\n', i, obj_fcn(i));
        %输出迭代次数和函数的结果
    end
    % check termination condition
    if i > 1,  %进化步长控制
        if abs(obj_fcn(i) - obj_fcn(i-1)) < min_impro, break; end,
    end
end
toc

%%%%%%证得如自定义图像中的MCR不能计算，故在此继续尝试直接用newing和A相比较

A = ones(height,width,1);
for i = 1:height
    for j = 1:width
        if (fix(a(i,j) / 85) == 1)
            A(i,j,1) = 2;
        end
        if (fix(a(i,j) / 85) == 2)
            A(i,j,1) = 3;
        end
        if (fix(a(i,j,1) / 85) == 3)
            A(i,j,1) = 4;
        end
    end
end    
A = reshape(A,1,data_n);

  newing = zeros(row,column);
for i=1:row
    for j=1:column         
        maxmembership=membership(i,j,1);
        index=1;
        for k=2:cluster_num            
            if(membership(i,j,k)>maxmembership)
                maxmembership=membership(i,j,k);
                index=k;
            end
        end
        newing(i,j) = round(255 * (1-(index-1)/(cluster_num-1)));
    end 
end

B = reshape(newing,1,data_n);
b = fix((max(B) - B(1,1)) / cluster_num);
for i = 2:data_n
    if B(1,i) == B(1,1)
        B(1,i) = 1;
    elseif (fix(B(1,i) / b) == 2)
        B(1,i) = 2;
    elseif (fix(B(1,i) / b)  == 3)
        B(1,i) = 3;
    else
        B(1,i) = 4;
    end
end
B(1,1) = 1;

sum = 0;
for i = 1:data_n
    if ( A(1,i) ~= B(1,i))
        sum = sum + 1;
    end
end
MCR = sum / data_n;
fprintf('MCR = %d\n',MCR);

S = 0;
for i = 1:data_n
    S = S + (A(1,i) - B(1,i)).^2;
end

RMS = sqrt(S / (data_n * (data_n -1)));
fprintf('RMS = %d\n',RMS);

figure(2);
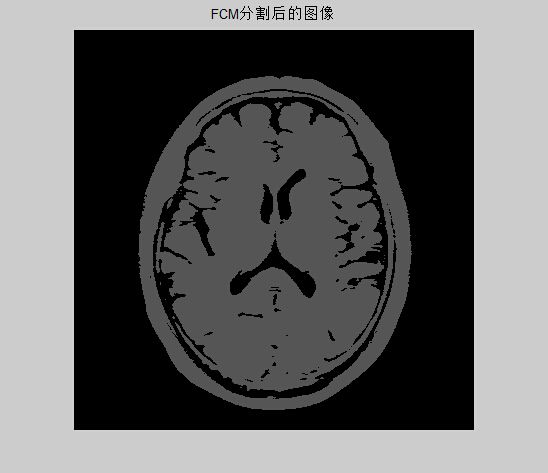
imshow((uint8(newing)));
title('FCM分割后的图像');   

结果如下：

转载自： http://www.cnblogs.com/ybjourney/p/4735335.html