李宏毅机器学习笔记(1)-Regression
李宏毅机器学习笔记(1)-Regression
视频来自李宏毅机器学习2017·1-Regression,笔记个人学习用
回归
回归:预测有“问题”,有“答案”的例子,如房价预测,“问题”就是有关房子的多个变量(面积,卧室数等等),“答案”就是最终的房价。
步骤
Step1:model
从众多的方程中选择合适的拟合方程:
y = w ⋅ x c p + b y=w·x_{cp}+b y=w⋅xcp+b
Step2:Goodness of Function
获得多组真实数据,分别包含输入与输出:
损失函数(loss function):input a function,output how bad it is
L ( f ) = ∑ i = 1 n ( y ^ n − f ( x c p n ) ) 2 L(f)=\sum_{i =1}^{n}({\hat{y}^n - f(x_{cp}^{n})})^2 L(f)=i=1∑n(y^n−f(xcpn))2
y ^ n \hat{y}^n y^n代表真实值, f ( x c p n ) f(x_{cp}^{n}) f(xcpn)代表预测值,如果写成w和b的形式就是:
L ( w , b ) = ∑ i = 1 n ( y ^ n − ( w ⋅ x c p n + b ) ) 2 L(w,b)=\sum_{i=1}^{n}(\hat{y}^n - (w·x_{cp}^{n}+b))^{2} L(w,b)=i=1∑n(y^n−(w⋅xcpn+b))2

Step3:Gradient Descent
使用梯度下降法可以使损失函数最小化,步骤如下:

假设只有一个参数 w w w
w = w − η d L d w ( i t e r a t i o n ) w = w -\eta\frac{dL}{dw} (iteration) w=w−ηdwdL(iteration)
其中 η \eta η叫做学习率(learning rate),他决定了学习速度(梯度下降速率)
如果有多个参数(如 w w w, b b b)
(1)随机选取w和b
(2)计算偏导数值
(3)多次迭代
w = w − η ∂ L ∂ w ( i t e r a t i o n ) w = w -\eta\frac{\partial L}{\partial w} (iteration) w=w−η∂w∂L(iteration)
b = b − η ∂ L ∂ b ( i t e r a t i o n ) b = b -\eta\frac{\partial L}{\partial b} (iteration) b=b−η∂b∂L(iteration)
梯度下降有可能达到全局收敛,也有可能达到局部收敛
梯度下降到局部最优与全局最优会停下,但是到达鞍点saddle point也会停下
结果
另外选取一些数据来做测试集:这里采用测试数据集计算得到的平均误差大于训练集属于正常现象

改进策略

可以适当使用多次向函数进行逼近,但是并不是function越复杂,次数越大拟合效果就越好,容易造成过拟合与欠拟合的发生,由图中可以看出使用三次函数的拟合效果最好。四次以上过拟合出现,三次以下欠拟合出现。
改进步骤:
(1)重新设计model(考虑种类(属性)进去)有了新的函数写法:

(2)Regularization正则化
y = b + ∑ w ⋅ x i y=b+\sum{}{}w·x_{i} y=b+∑w⋅xi
L = ∑ n ( y ^ n − ( b + ∑ w ⋅ x i ) ) 2 + λ ∑ ( w i ) 2 L=\sum_{n}(\hat{y}^{n}-(b+\sum{}{}w·x_{i}))^{2}+\lambda\sum{}{}(w_{i})^{2} L=n∑(y^n−(b+∑w⋅xi))2+λ∑(wi)2
这样可以使损失函数更加平滑(smooth):输入变化大时输出变化较小
为什么要选用更加平滑的函数:通常情况下认为函数越平滑,结果越有可能正确(避免挑选出“抖动”很厉害的model)
1. λ \lambda λ是一个需要手调的参数,如何调整见后续的讲解
2.不需要再偏置上加入正则项,偏置对函数的平滑影响可以忽略
Regression Demo
ERROR来自哪里?–bias and variance(方差)
bias代表距离中心的距离,即预测值距离真实值的距离;variance代表预测值的散布程度。通俗说法就是bias代表准,variance代表集中,最好的情况是打的准分布又集中。诊断错误的来源可以挑选适当的方法,从而更好地优化模型。
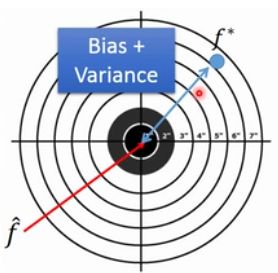
举例来说,为了预测一组样本的期望 μ \mu μ和方差 σ 2 \sigma^{2} σ2,取到了N个样本点 x 1 . . x n {x_{1}..x_{n}} x1..xn,估计 μ \mu μ则有:
m = 1 N ∑ i = 1 N x i ≠ μ m=\frac{1}{N}\sum_{i=1}^{N}x_{i}\neq\mu m=N1i=1∑Nxi̸=μ
选择不同的样本数据会得到不同的样本均值,样本均值都散布在期望周围。
E ( m ) = E ( 1 N ∑ i = 1 N x i ) = 1 N ∑ i = 1 N E ( x i ) = μ E(m)=E(\frac{1}{N}\sum_{i=1}^{N}x_{i})=\frac{1}{N}\sum_{i=1}^{N}E(x_{i})=\mu E(m)=E(N1i=1∑Nxi)=N1i=1∑NE(xi)=μ
估计 σ 2 \sigma^{2} σ2时有 m = 1 N ∑ i = 1 N x i , S 2 = 1 N ∑ i = 1 N ( x i − m ) 2 m=\frac{1}{N}\sum_{i=1}^{N}x_{i},\quad S^{2}=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-m)^{2} m=N1i=1∑Nxi,S2=N1i=1∑N(xi−m)2
E ( S 2 ) = N − 1 N σ 2 ≠ σ 2 E(S^{2})=\frac{N-1}{N}\sigma^{2}\neq\sigma^{2} E(S2)=NN−1σ2̸=σ2

从图中可以看出来,越简单的model受数据影响越小,它的variance也就越集中,但是它的biases越大;越复杂的model受数据影响就越大,分散程度也就越大。但是它的bias越小。可以用一张图形象地说明模型的复杂程度与bias和variance的关系:如果误差出现在bias,就是欠拟合;误差出现在variance,就是过拟合

诊断
1.如果model没有很好地拟合数据,即所预测出来的回归方程直线距离真实值还有一段差距,那么就是bias过大–欠拟合
2.如果model可以拟合training data得到一个小的error,但是在testing data中得到了一个大的error,这种情况有可能是variance较大–过拟合
措施
1.bias比较大:从上面的小图可以看到,数据没有“包括中心点target”
(1)增加更多的features
(2)使model更加复杂
2.variance比较大:
(1)增加你的数据(有效但是不经常实用)
(2)正则化Regularization
补充内容:最小二乘算法
上面内容说道,如果模型没有很好地拟合数据,就会出现真实数据点和拟合函数曲线之间存在“距离”。注意这个距离并不是垂直距离,在后续《计量经济学》课程学习介绍最小二乘估计中了解到,“距离”学名为残差。
最小二乘法是一种经典的机器学习算法,它是一种通过最小化残差平方和来进行未知参数估计的方法:(图片来自百度)
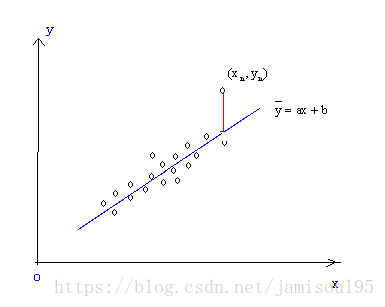
如图,我们首先规定一下函数符号,假设图中的数据点为 ( x i , y i ) (x_{i},y_{i}) (xi,yi),横坐标 x n x_{n} xn对应的预测出来的回归方程上的点的纵坐标为 y i ^ \hat{y_{i}} yi^,则图中红色线段的距离就是残差,数学表示为: e i = Y i − Y i ^ e_{i}=Y_{i}-\hat{Y_{i}} ei=Yi−Yi^
样本的回归模型是: Y = β 0 ^ + β 1 ^ X i + e i Y=\hat{\beta_{0}}+\hat{\beta_{1}}X_{i}+e_{i} Y=β0^+β1^Xi+ei则有 e i = Y − β 0 ^ − β 1 ^ X i e_{i}=Y-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i} ei=Y−β0^−β1^Xi预测方程是: Y ^ = β 0 ^ + β 1 ^ X i \hat{Y}=\hat{\beta_{0}}+\hat{\beta_{1}}X_{i} Y^=β0^+β1^Xi注意如果Y头上加了个“帽子”代表预测值,此时方程就不能加上 e i e_{i} ei。
欠拟合问题使得残差存在,我们优化的目标就是让这些残差的和最小,但是问题出现了: ( y n − y n ^ ) (y_{n}-\hat{y_{n}}) (yn−yn^)有正有负,那么就存在一种极端情况,残差和为零,问题就变得不可优化了。所以我们采用残差平方和的表示方式,那么优化的目标就是最小化残差平方和:
Q = arg min β 0 , β 1 ^ ^ ∑ e i 2 Q=\mathop{\arg\min}_{\hat{\beta_{0},\hat{\beta_{1}}}}\sum{}{}{e_{i}}^{2} Q=argminβ0,β1^^∑ei2
其中arg表示使目标函数取最小(最大)时的变量的取值,也就是我们要预测的 β 0 ^ 、 β 1 ^ \hat{\beta_{0}}、\hat{\beta_{1}} β0^、β1^,将他们看作变量,则原问题转化为二元函数求极值,它的充分条件即一阶偏导数等于0,于是有了关于他们两个的二元一次方程组:从而解出两个变量。
{ ∂ Q ∂ β 0 ^ = 2 ∑ i = 1 n ( Y − β 0 ^ − β 1 ^ X i ) ( − 1 ) = 0 ∂ Q ∂ β 1 ^ = 2 ∑ i = 1 n ( Y − β 0 ^ − β 1 ^ X i ) ( − X i ) = 0 \begin{cases} \frac{\partial Q}{\partial \hat{\beta_{0}}}=2\sum_{i=1}^{n}(Y-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i})(-1)=0 \\ \\ \frac{\partial Q}{\partial \hat{\beta_{1}}}=2\sum_{i=1}^{n}(Y-\hat{\beta_{0}}-\hat{\beta_{1}}X_{i})(-X_{i})=0 \\ \end{cases} ⎩⎪⎪⎨⎪⎪⎧∂β0^∂Q=2∑i=1n(Y−β0^−β1^Xi)(−1)=0∂β1^∂Q=2∑i=1n(Y−β0^−β1^Xi)(−Xi)=0
你不应该做的事情

用手中有的数据分为训练数据和测试数据,然后任意选择若干个模型导入训练数据训练,再用测试数据进行检验,选择使用误差最小的模型,这样做欠妥当,因为所谓的“training data”和“testing data”是你手头现有的数据分成的两个部分,而真正的testing data是你手头没有的,误差较小的模型放到真正的testing data上面不一定有较好的表现
正确的做法:交叉验证(crossing validation)
做法
将训练数据分为training data和validation data,使用training data来训练model,使用validation来验证选择model。如图validation在model3的误差最小,选择model3如果不放心,还可以将全部的training data放到model3中再training一次。

K-fold crossing validation

一部分数据作为train,另一部分作为val;再更换train和val,分别计算模型的性能,最后分别根据模型求性能平均值,选出合适的模型(K通常情况下取10)
Python编程练习参考CSDN博主yueguizhilin的文章:机器学习练习(三)——交叉验证Cross-validation
