R语言时间序列分析

原文：http://a-little-book-of-r-for-time-series.readthedocs.org/en/latest/src/timeseries.html

作者：Avril Coghlan Email：[email protected] 

中文档由梁德明、赵华蕾合译；联系方式：[email protected]；内容遵循许可协议CC 3.0 BY

中文档PDF版本地址为：http://doc.datapanda.net/a-Little-Book-of-R-for-Time-Series.pdf

本文在原中文文档的基础上，增加了部分新分析功能，并修正了原文中自定义函数的错误！

R语言时间序列初探！

读取时间序列数据

kings<-scan("http://robjhyndman.com/tsdldata/misc/kings.dat",skip=3)
kings
##  [1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69
## [24] 59 48 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56
# 在这个案例中有42位英国国王的去世年龄数据被读入到变量”kings”中。
# 一旦你将时间序列数据读入到R，下一步便是将数据存储到R中的一个时间序列对象里，以便你能使用R的很多函数分析时间序列数据。我们在R中使# 用ts()函数将数据存储到一个时间序列对象中去。例如存储“kings”这个变量中的数据到时间序列对象中，我们输入以下代码：
kingstimeseries<-ts(kings)
kingstimeseries
## Time Series:
## Start = 1 
## End = 42 
## Frequency = 1 
##  [1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69
## [24] 59 48 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56
# 有时候时间序列数据集是少于一年的间隔相同的数据，比如月度或者季度数据。在这种情况下，你可以使用ts()函数中的“frequency”参数指定收# 集数据在一年中的频数。如月度数据就设定frequency=12，季度数据就设定frequency=4。
# 你也可以通过ts()函数中的“start”参数来指定收集数据的第一年和这一年第一个间隔期。例如，如果你想指定第一个时间点为1986年的第二个季# 度，你只需设定start=c(1986,2)。
# 一个样本数据集是从1946年1月到1959年12月的纽约每月出生人口数量（由牛顿最初收集）数据集可以从此链接下载（http://robjhyndman.com# # /tsdldata/data/nybirths.dat）。我们将数据读入R，并且存储到一个时间序列对象中，输入以下代码：
births<-scan("http://robjhyndman.com/tsdldata/data/nybirths.dat")
birthstimeseries<-ts(births,frequency = 12,start=c(1946,1))
birthstimeseries
##         Jan    Feb    Mar    Apr    May    Jun    Jul    Aug    Sep    Oct
## 1946 26.663 23.598 26.931 24.740 25.806 24.364 24.477 23.901 23.175 23.227
## 1947 21.439 21.089 23.709 21.669 21.752 20.761 23.479 23.824 23.105 23.110
## 1948 21.937 20.035 23.590 21.672 22.222 22.123 23.950 23.504 22.238 23.142
## 1949 21.548 20.000 22.424 20.615 21.761 22.874 24.104 23.748 23.262 22.907
## 1950 22.604 20.894 24.677 23.673 25.320 23.583 24.671 24.454 24.122 24.252
## 1951 23.287 23.049 25.076 24.037 24.430 24.667 26.451 25.618 25.014 25.110
## 1952 23.798 22.270 24.775 22.646 23.988 24.737 26.276 25.816 25.210 25.199
## 1953 24.364 22.644 25.565 24.062 25.431 24.635 27.009 26.606 26.268 26.462
## 1954 24.657 23.304 26.982 26.199 27.210 26.122 26.706 26.878 26.152 26.379
## 1955 24.990 24.239 26.721 23.475 24.767 26.219 28.361 28.599 27.914 27.784
## 1956 26.217 24.218 27.914 26.975 28.527 27.139 28.982 28.169 28.056 29.136
## 1957 26.589 24.848 27.543 26.896 28.878 27.390 28.065 28.141 29.048 28.484
## 1958 27.132 24.924 28.963 26.589 27.931 28.009 29.229 28.759 28.405 27.945
## 1959 26.076 25.286 27.660 25.951 26.398 25.565 28.865 30.000 29.261 29.012
##         Nov    Dec
## 1946 21.672 21.870
## 1947 21.759 22.073
## 1948 21.059 21.573
## 1949 21.519 22.025
## 1950 22.084 22.991
## 1951 22.964 23.981
## 1952 23.162 24.707
## 1953 25.246 25.180
## 1954 24.712 25.688
## 1955 25.693 26.881
## 1956 26.291 26.987
## 1957 26.634 27.735
## 1958 25.912 26.619
## 1959 26.992 27.897
# 查看开始日期
start(birthstimeseries)
## [1] 1946    1
# 查看结束日期
end(birthstimeseries)
## [1] 1959   12
# 查看一个周期的频数
frequency(birthstimeseries)
## [1] 12
# 同样的，这个文件（http://robjhyndman.com/tsdldata/data/fancy.dat ）包含着一家位于昆士兰海滨度假圣地的纪念品商店从1987年1月到198# 7年12月的每月销售数据（原始数据源于Wheelwright and Hyndman，1998）。我们将数据读入R使用以下代码：
souvenir<-scan("http://robjhyndman.com/tsdldata/data/fancy.dat")
souvenirtimeseries<-ts(souvenir,frequency = 12,start=c(1987,1))
souvenirtimeseries
##            Jan       Feb       Mar       Apr       May       Jun       Jul
## 1987   1664.81   2397.53   2840.71   3547.29   3752.96   3714.74   4349.61
## 1988   2499.81   5198.24   7225.14   4806.03   5900.88   4951.34   6179.12
## 1989   4717.02   5702.63   9957.58   5304.78   6492.43   6630.80   7349.62
## 1990   5921.10   5814.58  12421.25   6369.77   7609.12   7224.75   8121.22
## 1991   4826.64   6470.23   9638.77   8821.17   8722.37  10209.48  11276.55
## 1992   7615.03   9849.69  14558.40  11587.33   9332.56  13082.09  16732.78
## 1993  10243.24  11266.88  21826.84  17357.33  15997.79  18601.53  26155.15
##            Aug       Sep       Oct       Nov       Dec
## 1987   3566.34   5021.82   6423.48   7600.60  19756.21
## 1988   4752.15   5496.43   5835.10  12600.08  28541.72
## 1989   8176.62   8573.17   9690.50  15151.84  34061.01
## 1990   7979.25   8093.06   8476.70  17914.66  30114.41
## 1991  12552.22  11637.39  13606.89  21822.11  45060.69
## 1992  19888.61  23933.38  25391.35  36024.80  80721.71
## 1993  28586.52  30505.41  30821.33  46634.38 104660.67
Plotting Time Series绘制时间序列图

# 一旦我们将时间序列读入R，下一步通常是用这些数据绘制时间序列图，我们可以使用R中的plot.ts()函数。 例如，绘制英国国王（依次的）去世年龄数据的时间序列图，我们输入代码：
plot.ts(kingstimeseries) # 等价于plot(kingstimeseries)
# 还可以增加线性拟合曲线
abline(lm(kingstimeseries~time(kingstimeseries)))




# 从时间曲线图可以看出，这个时间序列可以用相加模型来描述，因为在这一段时间内的随机变动大致是不变的。
# 同样的，我们画一个纽约每月出生人口数量的时间序列图，输入代码：
plot.ts(birthstimeseries)
# 增加线性拟合曲线
abline(lm(birthstimeseries~time(birthstimeseries)),col="red")




# 我们可以看到这个时间序列在一定月份存在的季节性变动：在每年的夏天都有一个出生峰值，在冬季的时候进入波谷。同样，这样的时间序列也可# 能是一个相加模型，随着时间推移，季节性波动时大致稳定的而不是依赖于时间序列水平，且对着时间的变化，随机波动看起来也是大致稳定的。
分解时间序列


分解一个时间序列意味着把它拆分成构成元件，一般序列包含一个趋势部分、一个不规则部分，如果是一个季节性时间序列，则还有一个季节性部分。
分解非季节性数据
一个非季节性时间序列包含一个趋势部分和一个不规则部分。
为了估计出一个非季节性时间序列的趋势部分，使之能够用相加模型进行描述，最常用的方法便是平滑法，比如计算时间序列的简单移动平均。
在R的“TTR”包中的SMA()函数可以用简单的移动平均来平滑时间序列数据
library(TTR)
## Loading required package: xts
## Loading required package: zoo
## 
## Attaching package: 'zoo'
## 
## The following objects are masked from 'package:base':
## 
##     as.Date, as.Date.numeric
# 使用SMA()函数时，你需要通过参数“n”指定来简单移动平均的跨度
# 例如如上所述的，这个42位英国国王的去世年龄数据呈现出非季节性，并且由于其随机变动在整个时间段内是大致不变的，这个序列也可以被描述称为一个相加模型。
# 因此，我们可以尝试使用简单移动平均平滑来估计趋势部分。我们使用跨度为3的简单移动平均平滑时间序列数据，并且作图，代码如下：
kingstimeseriesSMA3<-SMA(kingstimeseries,n=3)
plot.ts(kingstimeseriesSMA3)




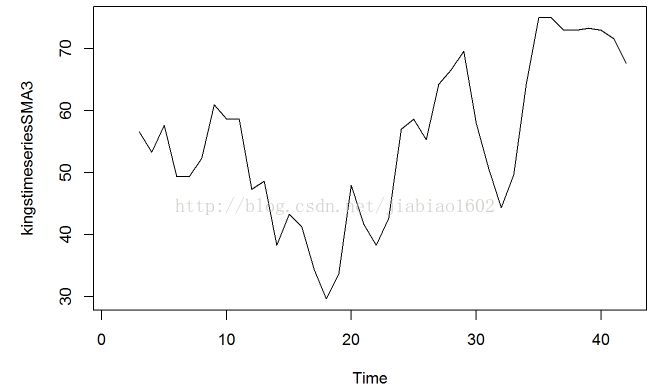
# 当我们使用跨度为3的简单移动平均平滑后，时间序列依然呈现出大量的随便波动。因此，为了更加准确地估计这个趋势部分，我们也许应该尝试下更大的跨度进行平滑。
kingstimeseriesSMA8<-SMA(kingstimeseries,n=8)
plot.ts(kingstimeseriesSMA8)




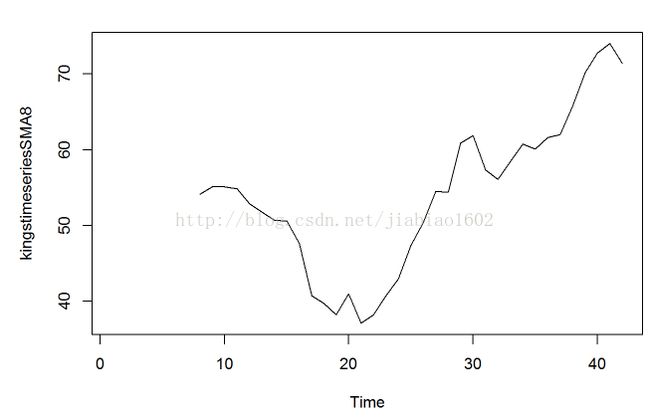
# 这个跨度为8的简单移动平均平滑数据的趋势部分看起来更加清晰了，我们可以发现这个时间序列前20为国王去世年龄从最初的55周岁下降到38周岁，然后一直上升到第40届国王的73周岁。
分解季节性数据


一个季节性时间序列包含一个趋势部分，一个季节性部分和一个不规则部分。分解时间序列就意味着要把时间序列分解称为这三个部分：也就是估计出这三个部分。
对于可以使用相加模型进行描述的时间序列中的趋势部分和季节性部分，我们可以使用R中“decompose()”函数来估计。这个函数可以估计出时间序列中趋势的、季节性的和不规则的部分，而此时间序列须是可以用相加模型描述的。
# 例如前文所述的，纽约每月出生人口数量是在夏季有峰值、冬季有低谷的时间序列，当在季节性和随机变动在真个时间段内看起来像大致不变的时候，那么此模型很有可能是可以用相加模型来描述。
# 为了估计时间序列的趋势的、季节性和不规则部分，输入代码：
birthstimeseriescomponents<-decompose(birthstimeseries)

plot(birthstimeseriescomponents)

 #### 季节性因素调整 + 如果这个季节性时间序列可以用相加模型来描述，你可以通过估计季节性部分修正时间序列，也可以从原始序列中去除掉估计得季节性部分。我们可以通过“decompose()”函数使用估计出的季节性部分进行计算。

# 例如，对纽约每月出生人口数量进行季节性修正，我们可以用“decompose()”估计季节性部分，也可以把这个部分从原始时间序列中去除。
birthstimeseriesseasonallyadjusted<-birthstimeseries-birthstimeseriescomponents$seasonal
# 我们可以使用“plot()”画出季节性修正时间序列，代码如下：
plot(birthstimeseriesseasonallyadjusted)




# 你可以看到这个去除掉季节性变动的修正序列。这个季节性修正后的时间序列现在仅包含趋势部分和不规则变动部分。
使用指数平滑法进行预测


指数平滑法可以用于时间序列数据的短期预测。
简单指数平滑法


如果你有一个可用相加模型描述的，并且处于恒定水平和没有季节性变动的时间序列，你可以使用简单指数平滑法对其进行短期预测。
简单指数平滑法提供了一种方法估计当前时间点上的水平。为了准确的估计当前时间的水平，我们使用alpha参数来控制平滑。Alpha的取值在0到1之间。当alpha越接近0的时候，临近预测的观测值在预测中的权重就越小。
# 例如，这个文件（ http://robjhyndman.com/tsdldata/hurst/precip1.dat）包含了伦敦从1813年到1912年全部的每年每英尺降雨量（初始数据来自Hipel and McLeod, 1994）。我们可以将这些数据读入R并且绘制时序图，代码如下：
rain<-scan("http://robjhyndman.com/tsdldata/hurst/precip1.dat",skip=1)
rainseries <- ts(rain,start=c(1813))
plot.ts(rainseries)
abline(lm(rainseries~time(rainseries)),col="green")




# 从这个图可以看出整个曲线处于大致不变的水平（意思便是大约保持的25英尺左右）。其随机变动在整个时间序列的范围内也可以认为是大致不变的，所以这个序列也可以大致被描述成为一个相加模型。因此，我们可以使用简单指数平滑法对其进行预测。
# 为了能够在R中使用简单指数平滑法进行预测，我们可以使用R中的“HoltWinters()”函数对预测模型进行修正。为了能够在指数平滑法中使用HotlWinters()，我们需要在HoltWinters()函数中设定参数beta=FALSE和gamma=FALSE（beta和gamma是Holt指数平滑法或者是Holt-Winters指数平滑法的参数，如下所述）。
# HoltWinters()函数返回的是一个变量列表，包含了一些元素名。
# 比如，使用简单指数平滑发对伦敦每年下雨量进行预测，代码如下：
rainseriesforecasts<-HoltWinters(rainseries,beta=FALSE,gamma=FALSE)
rainseriesforecasts
## Holt-Winters exponential smoothing without trend and without seasonal component.
## 
## Call:
## HoltWinters(x = rainseries, beta = FALSE, gamma = FALSE)
## 
## Smoothing parameters:
##  alpha: 0.02412151
##  beta : FALSE
##  gamma: FALSE
## 
## Coefficients:
##       [,1]
## a 24.67819
# HoltWinters()的输出告诉我们alpha参数的估计值约为0.024。这个数字非常接近0，告诉我们预测是基于最近的和较远的一些观测值（尽管更多的权重在现在的观测值上）。
# 默认的时候，HoltWinters()默认仅给出在原始时间序列所覆盖时期内的预测。在本案例中，原始时间序列包含伦敦1813-1912年降雨量，因此预测的时段也是1813-1912年。
# 在上面案例中，我们将HoltWinters()函数的输出结果存储在“rainseriesforecasts”这个列表变量里。这个HoltWinters()产生的预测呗存储在一个元素名为“fitted”的列表变量里，我们可以通过以下代码获得这些值：
# rainseriesforecasts$fitted
# 我们可以再画出原始时间序列和预测的，代码如下：
plot(rainseriesforecasts)




# 这个图用黑色画出了原始时间序列图，用红色画出了预测的线条。在这里，预测的时间序列比原始时间序列数据平滑非常多。
# 作为预测准确度的一个度量，我们可以计算样本内预测误差的误差平方之和，即原始时间序列覆盖的时期内的预测误差。这个误差平方法将存储在一个元素名为“rainseriesforecasts”（我们称之为“SSE”）的列表变量里，我们通过以下代码获取这些值：
rainseriesforecasts$SSE
## [1] 1828.855
# 也就是说，这里的误差平方和是1828.855。
# 用时间序列的第一个值作为这个水平的初始值在简单指数平滑法中常见的操作。例如，在伦敦降雨量这个时间序列里，第一个值为1813年的23.56（英尺）。你可以在HoltWinters()函数中使用“l.start”参数指定其味初始值。例如，我们将预测的初始值水平设定为23.56，代码如下：
HoltWinters(rainseries, beta=FALSE, gamma=FALSE, l.start=23.56)
## Holt-Winters exponential smoothing without trend and without seasonal component.
## 
## Call:
## HoltWinters(x = rainseries, beta = FALSE, gamma = FALSE, l.start = 23.56)
## 
## Smoothing parameters:
##  alpha: 0.02412151
##  beta : FALSE
##  gamma: FALSE
## 
## Coefficients:
##       [,1]
## a 24.67819
# 如上所说，HoltWinters()的默认仅仅是预测时期即覆盖原始数据的时期，像上面的1813-1912年的降雨量数据。我们可以使用R中的“forecast”包中的“forecast.HoltWinters()”函数进行更远时间点上的预测。
library(forecast)
## Loading required package: timeDate
## This is forecast 5.8
# 你可以使用forecast.HoltWinters()中的参数”h”来制定你想要做多少时间点的预测。例如，要使用forecast.HoltWinters()做1814-1820年（之后8年）的下雨量预测，我们输入：
rainseriescasts2<-forecast.HoltWinters(rainseriesforecasts,h=8)
rainseriescasts2
##      Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
## 1913       24.67819 19.17493 30.18145 16.26169 33.09470
## 1914       24.67819 19.17333 30.18305 16.25924 33.09715
## 1915       24.67819 19.17173 30.18465 16.25679 33.09960
## 1916       24.67819 19.17013 30.18625 16.25434 33.10204
## 1917       24.67819 19.16853 30.18785 16.25190 33.10449
## 1918       24.67819 19.16694 30.18945 16.24945 33.10694
## 1919       24.67819 19.16534 30.19105 16.24701 33.10938
## 1920       24.67819 19.16374 30.19265 16.24456 33.11182
# forecast.HoltWinters()函数给出了一年的预测，一个80%的预测区间和一个95%的预测区间的两个预测。例如，1920年的下雨量预测为24.68英寸，95%的预测区间为(16.24, 33.11)。
# 为了画出forecast.HoltWinters()的预测结果，我们可以使用“plot.forecast()”函数：
plot.forecast(rainseriescasts2)




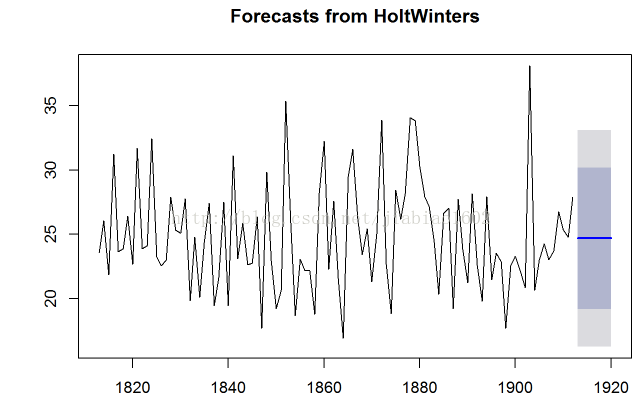
# 这的蓝色线条是预测的1913-1920的降雨量，橙色阴影区域为80%的预测区间，黄色阴影区域为95%的预测区间。
# 使用forecast.HoltWinters()返回的样本内预测误差将被存储在一个元素名为“residuals”的列表变量中。如果预测模型不可再被优化，连续预测中的预测误差是不相关的。换句话说，如果连续预测中的误差是相关的，很有可能是简单指数平滑预测可以被另一种预测技术优化。
# 为了验证是否如此，我们获取样本误差中1-20阶的相关图。我们可以通过R里的“acf()”函数计算预测误差的相关图。为了指定我们想要看到的最大阶数，可以使用acf()中的“lag.max”参数。
# 例如，为了计算伦敦降雨量数据的样本内预测误差延迟1-20阶的相关图，我们输入代码：
acf(rainseriescasts2$residuals,lag.max = 20)




# 你可以从样本相关图中看出自相关系数在3阶的时候触及了置信界限。为了验证在滞后1-20阶（lags 1-20）时候的非0相关是否显著，我们可以使用Ljung-Box检验。这可以通过R中的“Box.test()”函数实现。最大阶数我们可以通过Box.test()函数中的“lag”参数来指定。
# 例如，为了检验伦敦降雨量数据的样本内预测误差在滞后1-20阶（lags 1-20）是非零自相关的，我们输入代码：
Box.test(rainseriescasts2$residuals,lag=20,type="Ljung-Box")
## 
##  Box-Ljung test
## 
## data:  rainseriescasts2$residuals
## X-squared = 17.4008, df = 20, p-value = 0.6268
# 这里Ljung-Box检验统计量为17.4，并且P值是0.6，所以这是不足以证明样本内预测误差在1-20阶是非零自相关的。
# 为了确定预测模型不可继续优化，我们需要一个好的方法来检验预测误差是正态分布，并且均值为零，方差不变。为了检验预测误差是方差不变的，我们可以画一个样本内预测误差图：
plot.ts(rainseriescasts2$residuals)




# 这个图展现了在整个时间区域样本内预测误差似乎是大致不变的方差的，尽管时间序列的前期（1820-1830）的波动大小与后期（如1840-1850）相比略小。
# 为了检验预测误差是均值为零的正态分布，我们可以画出预测误差的直方图，并覆盖上均值为零、标准方差的正态分布的曲线图到预测误差上。为了实现这一，我们可以定义R中的“plotForecastErrors()”函数，如下：
plotForecastErrors<-function(forecasterrors){
  # make a red histogram of the forecast errors:
  mybinsize<-IQR(forecasterrors)/4
  mysd<-sd(forecasterrors)
  mymin<-min(forecasterrors)-mysd*3
  mymax<-max(forecasterrors)+mysd*3
  mybins<-seq(mymin,mymax,mybinsize)
  hist(forecasterrors,col="red",freq=FALSE,breaks=mybins)
  # freq=FALSE ensures the area under the histogram = 1
  # generate normally distributed data with mean 0 and standard deviation mysd
  mynorm<-rnorm(10000,mean=0,sd=mysd)
  myhist<-hist(mynorm,plot=FALSE,breaks=mybins)
  # plot the normal curve as a blue line on top of the histogram of forecast errors:
  points(myhist$mids,myhist$density,type="l",col="blue",lwd=2)
}
# 然后你可以使用plotForecastErrors()画降雨量预测的预测误差直方图（和附着在上面的正太曲线）：
plotForecastErrors(rainseriescasts2$residuals)




# 这个图展现出预测误差大致集中分布在零附近，或多或少的接近正太分布，尽管图形看起来是一个偏向右侧的正态分布。然后，右偏是相对较小的，我们可以可以认为预测误差是服从均值为零的正态分布。
# 这个Ljung-Box检验告诉我们并不足以证明样本内预测误差是非零自相关的，预测误差的分布看起来似乎也是零均值的正态分布。这暗示我们这个简单指数平滑法为伦敦降雨提供了一个适当的预测模型，它是不能再被优化的。此外，假定基于80%和95%的预测区间是可能有效的（这里预测误差没有自相关系数，并且预测误差服从零均值，方差不变的正态分布）。 
霍尔特指数平滑法


如果你的时间序列可以被描述为一个增长或降低趋势的、没有季节性的相加模型，你可以使用霍尔特指数平滑法对其进行短期预测。
Holt指数平滑法估计当前时间点的水平和斜率。其平滑化是由两个参数控制的，alpha，用于估计当前时间点的水平，beta，用于估计当前时间点趋势部分的斜率。正如简单指数平滑法一样，alpha和beta参数都介于0到1之间，并且当参数越接近0，大多数近期的观测则将占据预测更小的权重。
# 一个可能可以用相加模型描述的有趋势的、无季节性的时间序列案例就是这1866年到1911年每年女人们裙子的直径。这个数据可以从该文件获得（http://robjhyndman.com/tsdldata/roberts/skirts.dat）（初始数据来自Hipel and McLeod, 1994）
skirts <- scan("http://robjhyndman.com/tsdldata/roberts/skirts.dat",skip=5)
skirtsseries<-ts(skirts,start=c(1866))
plot.ts(skirtsseries)




# 我们可以从此图看出裙子直径长度从1866年的600增加到1880的1050，并且在此之后有下降到1911年的520。
# 为了进行预测，我们使用R中的HoltWinters()函数对预测模型进行调整。为了使用HoltWinters()进行Holt指数平滑法，我们需要设定其参数gamma=FALSE（gamma参数常常用于Holt-Winters指数平滑法，后文将解释）
# 例如，为了使用Holt指数平滑法修正一个裙边直径的预测模型，我们输入代码：
skirtsseriesforecasts<-HoltWinters(skirtsseries,gamma=FALSE)
skirtsseriesforecasts
## Holt-Winters exponential smoothing with trend and without seasonal component.
## 
## Call:
## HoltWinters(x = skirtsseries, gamma = FALSE)
## 
## Smoothing parameters:
##  alpha: 0.8383481
##  beta : 1
##  gamma: FALSE
## 
## Coefficients:
##         [,1]
## a 529.308585
## b   5.690464
skirtsseriesforecasts$SSE
## [1] 16954.18
# 这里的alpha预测值为0.84，beta预测值为1.00。这都是非常高的值，告诉我们无论是水平上，还是趋势的斜率，当前值大部分都基于时间序列上最近的观测值。这样的直观感觉很好，因为其时间序列上的水平和斜率在整个时间段发生了巨大的变化。预测样本内误差的误差平方和是16954。
# 我们可以用黑色线条画出原始时间序列分布，用红色线条画出顶部的预测值，代码如下：
plot(skirtsseriesforecasts)




# 从该图我们可以看到样本内预测非常接近观测值，尽管他们对观测值来说有一点点延迟。
# 如果你想的话，你可以通过HoltWinters()函数中的“l.start”和“b.start”参数去指定水平和趋势的斜率的初始值。常见的设定水平初始值是让其等于时间序列的第一个值（在裙子数据中是608），而斜率的初始值则是其第二值减去第一个值（在裙子数据中是9）。
# 例如，为了使用Holt指数平滑法找到一个在裙边直径数据中合适的预测模型，我们设定其水平初始值为608，趋势部分的斜率初始值为9，代码如下：
HoltWinters(skirtsseries,gamma=FALSE,l.start = skirtsseries[1],b.start = skirtsseries[2]-skirtsseries[1])
## Holt-Winters exponential smoothing with trend and without seasonal component.
## 
## Call:
## HoltWinters(x = skirtsseries, gamma = FALSE, l.start = skirtsseries[1],     b.start = skirtsseries[2] - skirtsseries[1])
## 
## Smoothing parameters:
##  alpha: 0.8346775
##  beta : 1
##  gamma: FALSE
## 
## Coefficients:
##         [,1]
## a 529.278637
## b   5.670129
# 正如我们的简单指数平滑法一样，我们可以使用“forecast”包中的forecast.HoltWinters()函数预测未来时间而无需覆盖原始序列。
# 例如，我们的现在有的1866年到1911年的裙边直径时间序列数据，因此我们可以预测1912年到1930年（19个点或者更多），并且画出他们，代码如下：
skirtsseriescasts2<-forecast.HoltWinters(skirtsseriesforecasts,h=19)
plot.forecast(skirtsseriescasts2)




# 和简单指数平滑法一样，我们瞧瞧样本内预测误差是否在延迟1-20阶时是非零自相关的，以此来检验模型是否还可以被优化。
# 如裙边数据中，我们可以创建一个相关图，进行Ljung-Box检验，代码如下：
acf(skirtsseriescasts2$residuals,lag.max = 20)




Box.test(skirtsseriescasts2$residuals,lag=20,type="Ljung-Box")
## 
##  Box-Ljung test
## 
## data:  skirtsseriescasts2$residuals
## X-squared = 19.7312, df = 20, p-value = 0.4749
# 这个相关图呈现出样本内预测误差的样本自相关系数在滞后5阶的时候超过了置信边界。不管怎样，我们可以界定在前20滞后期中有1/20的自相关值超出95%的显著边界是偶然的，当我们进行Ljung-Box检验时，P值为0.47，意味着我们是不足以证明样本内预测误差在滞后1-20阶的时候是非零自相关的。
# 和简单指数平滑法一样，我们应该检查整个序列中的预测误差是否是方差不变、服从零均值正态分布的。
# 我们可以画出一个时间段预测误差图，和一个附上正太曲线的预测误差分布的直方图：
plot.ts(skirtsseriescasts2$residuals)




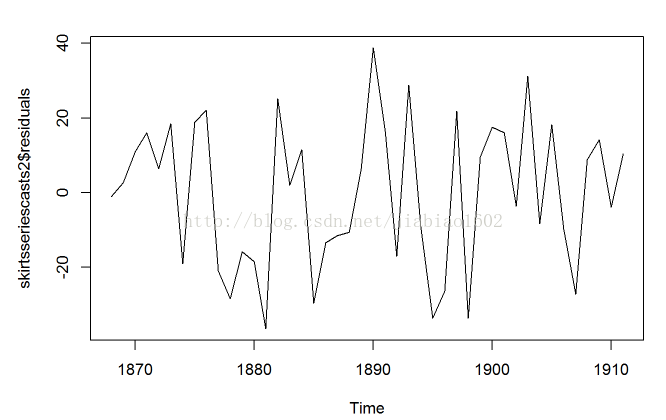
plotForecastErrors(skirtsseriescasts2$residuals)




# 这个预测误差的时间曲线图告诉我们预测误差在整个时间段内是大致方差不变的。这个预测误差的直方图告诉我们预测误差似乎是零均值、方差不变的正态分布。
# 因此，Ljung-Box检验告诉我们这是不足以证明预测误差是自相关的，而其预测误差的时间曲线图和直方图表示出似乎预测误差是服从零均值、方差不变的正态分布的。因此，我们可以总结这Holt指数平滑法为裙边直径提供了一个合适的预测，并且是不可再优化的。另外，这也意味着基于80%预测区间和95%预测区间的假设是非常合理的。
Holt-Winters指数平滑法


如果你有一个增长或降低趋势并存在季节性可被描述成为相加模型的时间序列，你可以使用霍尔特-温特指数平滑法对其进行短期预测。
Holt-Winters指数平滑法估计当前时间点的水平，斜率和季节性部分。平滑化依靠三个参数来控制：alpha，beta和gamma，分别对应当前时间点上的水平，趋势部分的斜率和季节性部分。参数alpha，beta和gamma的取值都在0和1之间，并且当其取值越接近0意味着对未来的预测值而言最近的观测值占据相对较小的权重。
# 一个可以用相加模型描述的并附有趋势性和季节性的时间序列案例，便是澳大利亚昆士兰州的海滨纪念品商店的月度销售日志。（上方讨论过）
# 为了实现预测，我们可以使用HoltWinters()函数对预测模型进行修正。比如，我们对纪念品商店的月度销售数据预测模型进行对数变换，代码如下：
logsouvenirtimeseries<-log(souvenirtimeseries)
souvenirtimeseriesforecasts<-HoltWinters(logsouvenirtimeseries)
souvenirtimeseriesforecasts
## Holt-Winters exponential smoothing with trend and additive seasonal component.
## 
## Call:
## HoltWinters(x = logsouvenirtimeseries)
## 
## Smoothing parameters:
##  alpha: 0.413418
##  beta : 0
##  gamma: 0.9561275
## 
## Coefficients:
##            [,1]
## a   10.37661961
## b    0.02996319
## s1  -0.80952063
## s2  -0.60576477
## s3   0.01103238
## s4  -0.24160551
## s5  -0.35933517
## s6  -0.18076683
## s7   0.07788605
## s8   0.10147055
## s9   0.09649353
## s10  0.05197826
## s11  0.41793637
## s12  1.18088423
souvenirtimeseriesforecasts$SSE
## [1] 2.011491
# 这里alpha，beta和gamma的估计值分别是0.41,0.00和0.96。alpha（0.41）是相对较低的，意味着在当前时间点估计得水平是基于最近观测和历史观测值。beta的估计值是0.00，表明估计出来的趋势部分的斜率在整个时间序列上是不变的，并且应该是等于其初始值。这是很直观的感觉，水平改变非常多，但是趋势部分的斜率b却仍然是大致相同的。与此相反的，gamma的值（0.96）则很高，表明当前时间点的季节性部分的估计仅仅基于最近的观测值。
# 正如简单指数平滑法和Holt指数平滑法一样，我们用黑线画出原始数据的时间曲线图，用红线在上面画出预测值的时间曲线图：
plot(souvenirtimeseriesforecasts)




# 我们可以从途中看出Holt-Winters指数平滑法是非常成功得预测了季节峰值，其峰值大约发生在每年的11月份。
# 为了预测非原始时间序列的未来一段时间，我们使用“forecast”包中的“forecast.HoltWinters()”函数。
# 例如，纪念品销售的原始数据是1987年1月到1993年12月。如果我们想预测1994年1月到1998年12月（48月或者更多），并且画出预测，代码如下：
souvenirtimeseriesforecasts2<-forecast.HoltWinters(souvenirtimeseriesforecasts,h=48)
plot.forecast(souvenirtimeseriesforecasts2)




# 我们可以通过画相关图和进行Ljung-Box检验来检查样本内预测误差在延迟1-20阶时否是非零自相关的，并以此确定预测模型是否可以再被优化
acf(souvenirtimeseriesforecasts2$residuals,lag.max=20)




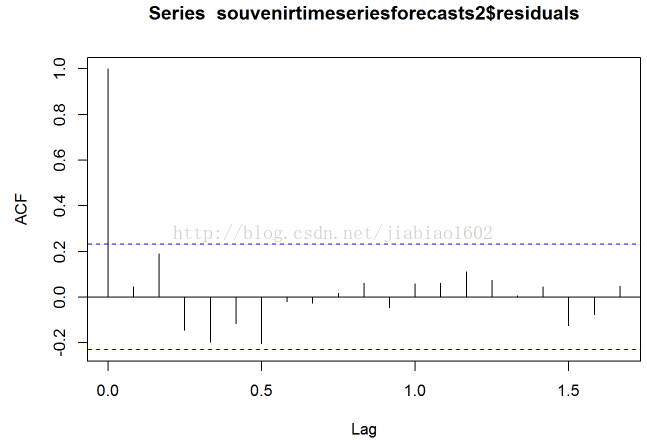
Box.test(souvenirtimeseriesforecasts2$residuals,lag=20,type="Ljung-Box")
## 
##  Box-Ljung test
## 
## data:  souvenirtimeseriesforecasts2$residuals
## X-squared = 17.5304, df = 20, p-value = 0.6183
# 这个样本内预测误差的相关图并没有在延迟1-20阶内自相关系数超过置信界限的。而且，Ljung-Box检验的P值是0.6，意味着是不足以证明延迟1-20阶是非零自相关的。
# 我们可以在整个时间段内检验预测误差是否是方差不变，并且服从零均值正态分布的。方法是画出预测误差的时间曲线图和直方图（并覆盖上正太曲线）：
plot.ts(souvenirtimeseriesforecasts2$residuals) # make a time plot




plotForecastErrors(souvenirtimeseriesforecasts2$residuals)  # make a histogram




# 从这个时间曲线图，它似乎告诉我们预测误差在整个时间段是方差不变的。从预测误差的直方图，似乎其预测误差是服从均值为零的正态分布的。
# 因此 ，这是不足以证明预测误差 ，这是不足以证明预测误差 ，这是不足以证明预测误差 ，这是不足以证明预测误差 ，这是不足以证明预测误差 ，不变的正态分布。这 不变的正态分布。这 不变的正态分布。这 不变的正态分布。这 暗示着 暗示着 Holt Holt-WintersWintersWinters WintersWintersWinters指数平滑法为 指数平滑法为 指数平滑法为 纪念品商店的销售数据提供了一个合适预测模型 纪念品商店的销售数据提供了一个合适预测模型。 此外 ， 在假设条件下， 在假设条件下， 在假设条件下， 在假设条件下基于 预测 区间的假设 区间的假设 区间的假设 也是 合理 的。
ARIMA模型


指数平滑法对于预测来说是非常有帮助的，而且它对时间序列上面连续的值之间相关性没有要求。但是，如果你想使用指数平滑法计算出预测区间，那么预测误差必须是不相关的，而且必须是服从零均值、方差不变的正态分布。
即使指数平滑法对时间序列连续数值之间相关性没有要求，在某种情况下，我们可以通过考虑数据之间的相关性来创建更好的预测模型。自回归移动平均模型（ARIMA）包含一个确定（explicit）的统计模型用于处理时间序列的不规则部分，它也允许不规则部分可以自相关。
时间序列的差分


ARIMA模型为平稳时间序列定义的。因此，如果你从一个非平稳的时间序列开始，首先你就需要做时间序列差分直到你得到一个平稳时间序列。如果你必须对时间序列做d阶差分才能得到一个平稳序列，那么你就使用ARIMA(p,d,q)模型，其中d是差分的阶数。
在R中你可以使用diff()函数作时间序列的差分。例如，每年女人裙子边缘的直径做成的时间序列数据，从1866年到1911年在平均值上是不平稳的。随着时间增加，数值变化很大。
# 我们可以通过键入下面的代码来得到时间序列（数据存于“skirtsseries”）的一阶差分，并画出差分序列的图：
skirtsseriesdiff1<-diff(skirtsseries,differences=1)
plot.ts(skirtsseriesdiff1)




# 一阶差分时间序列结果（上图）的均值看起来并不平稳。因此，我们需要再次做差分，来看一下是否能得到一个平稳时间序列：
skirtsseriesdiff2<-diff(skirtsseries,differences=2)
plot.ts(skirtsseriesdiff2)




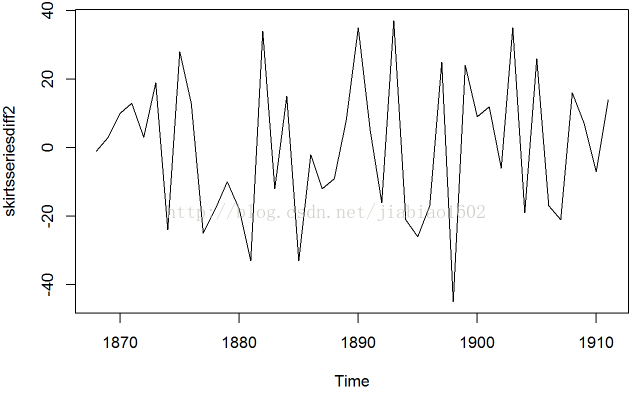
# 对于平稳性正式的检验称作“单位根测试”，可以在fUnitRoots包中得到
# 二次差分（上面）后的时间序列在均值和方差上确实看起来像是平稳的，随着时间推移，时间序列的水平和方差大致保持不变。因此，看起来我们需要对裙子直径进行两次差分以得到平稳序列。
# 如果你需要对你的原始时间序列数据做d阶差分来获得一个平稳时间序列，那么意味着你可以对你的时间序列使用ARIMA(p,d,q,)模型，其中d是差分的阶数。例如，对于女人裙子直径的时间序列，我们必须进行两次差分，所以差分的阶数就是2. 这意味着你可以使用ARIMA(p,2,q)模型。接下来我们需要找到ARIMA模型中的p值和q值。
# 另外一个时间序列的例子是英国（几位）国王依次去世年龄的时间序列(如图)
plot.ts(kingstimeseries)




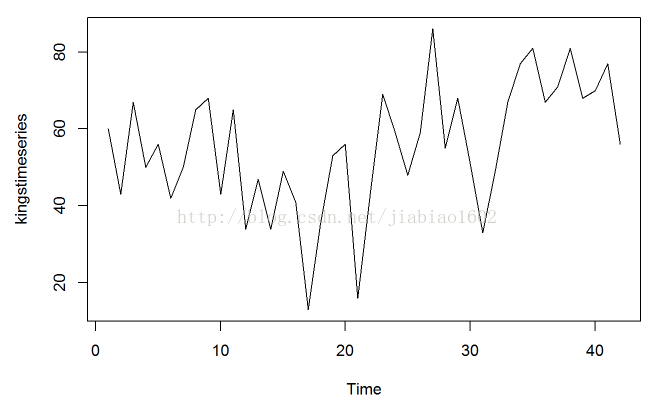
# 通过上面的时间曲线图我们可以看出，时间序列在平均值上并不平稳。为了计算时间序列的一阶差分并画出图形，我们输入如下命令：
kingstimeseriesdiff1<-diff(kingstimeseries,differences=1)
plot.ts(kingstimeseriesdiff1)




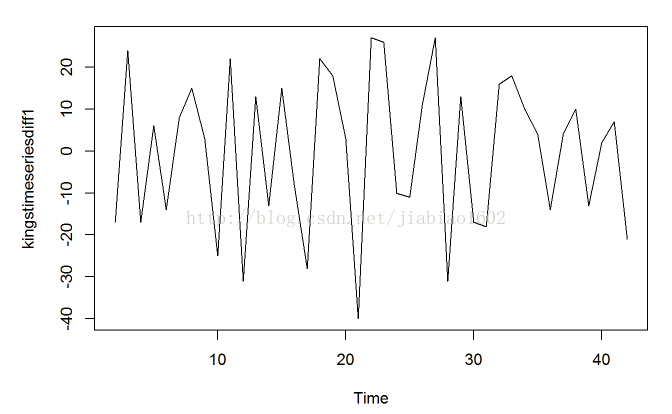
# 一阶差分的时间序列看起来在平均值和方差上是平稳的，所以对于英国国王（依次的）去世年龄时间序列使用ARIMA(p,1,q)模型是很适合的。通过一阶差分，我们去除了国王去世年龄序列的趋势部分，剩下了不规则的部分。现在我们可以检验不规则部分中邻项数值是否具有相关性；如果有的话，可以帮助我们建立一个预测模型来预测国王的年龄趋势。
选择一个合适的ARIMA模型


如果你的时间序列是平稳的，或者你通过做n次差分转化为一个平稳时间序列，接下来就是要选择合适的ARIMA模型，这意味着需要寻找ARIMA(p,d,q)中合适的p值和q值。为了得到这些，通常需要检查平稳时间序列的（自）相关图和偏相关图。
我们使用R中的“acf()”和“pacf”函数来分别（自）相关图和偏相关图。在“acf()”和“pacf设定“plot=FALSE”来得到自相关和偏相关的真实值。
# 英国国王去世年龄的例子
# 例如，要画出国王去世年龄一阶差分序列滞后1-20阶数（lags 1-20）的相关图，并且得到其自相关系数，我们输入：
acf(kingstimeseriesdiff1,lag.max=20)  #plot a correlogram




acf(kingstimeseriesdiff1,lag.max=20,plot=FALSE) # get the autocorrelation values
## 
## Autocorrelations of series 'kingstimeseriesdiff1', by lag
## 
##      0      1      2      3      4      5      6      7      8      9 
##  1.000 -0.360 -0.162 -0.050  0.227 -0.042 -0.181  0.095  0.064 -0.116 
##     10     11     12     13     14     15     16     17     18     19 
## -0.071  0.206 -0.017 -0.212  0.130  0.114 -0.009 -0.192  0.072  0.113 
##     20 
## -0.093
# 我们从上面相关图中可以看出在滞后1阶（lag1）的自相关值（-0.360）超出了置信边界，但是其他所有在滞后1-20阶（lags 1-20）的自相关值都没有超出置信边界。
# 要画出英国国王去世年龄在滞后1-20阶（lags 1-20）一阶差分时间序列的偏相关图，并得到偏相关的值，我们使用“pcf()”函数，输入：
pacf(kingstimeseriesdiff1,lag.max=20)  #plot a partial correlogram



pacf(kingstimeseriesdiff1,lag.max=20,plot=FALSE) # get the parital autocorrelation values
## 
## Partial autocorrelations of series 'kingstimeseriesdiff1', by lag
## 
##      1      2      3      4      5      6      7      8      9     10 
## -0.360 -0.335 -0.321  0.005  0.025 -0.144 -0.022 -0.007 -0.143 -0.167 
##     11     12     13     14     15     16     17     18     19     20 
##  0.065  0.034 -0.161  0.036  0.066  0.081 -0.005 -0.027 -0.006 -0.037
# 偏相关图显示在滞后1，2和3阶（lags 1,2,3）时的偏自相关系数超出了置信边界，为负值，且在等级上随着滞后阶数的增加而缓慢减少（lag 1：-0.360，lag 2：-0.335，lag 3：-0.321）。从lag 3之后偏自相关系数值缩小至0.
# 既然自相关值在滞后1阶（lag 1）之后为0，且偏相关值在滞后3阶（lag 3）之后缩小至 0，那么意味着接下来的ARIMA（自回归移动平均）模型对于一阶时间序列有如下性质：
## ARMA(3,0)模型：即偏自相关值在滞后3阶（lag 3）之后缩小至0且自相关值缩小至0（即使此模型中说自相关值缩小至0有些不太合适），则是一个阶层p=3自回归模型。 
## ARMA(0,1)模型：即自相关图在滞后1阶（lag 1）之后为0且偏自相关图缩小至0，则是一个阶数q=1的移动平均模型。
## ARMA(p,q)模型：即自相关图和偏相关图都缩小至0（即使此模型中说自相关图缩小至0有些不太合适），则是一个具有p和q大于0的混合模型。 
### 我们利用简单的原则来确定哪个模型是最好的：即我们认为具有最少参数的模型是最好的。ARMA(3,0)有3个参数，ARMA(0,1)有1个参数，而ARMA(p,q)至少有2个变量。因此ARMA(0,1)模型被认为是做好的模型。
### ARMA(0,1)模型是一阶的移动平均模型，或者称作MA(1)。这个模型可以写作：X_t - mu = Z_t - (theta * Z_t-1)，其中X_t是我们学习的平稳时间序列（英国国王去世年龄的一阶差分），mu是时间序列X_t的平均值，Z_t是具有平均值为0且方差为常数的白噪音，theta是可以被估计的参数。
### 移动平均模型通常用于建模一个时间序列，此序列具有邻项观察值之间短期相关的特征。直观地，可以很好理解MA模型可以用来描述英国国王去世年龄的时间序列中不规则的成分，比如我们可能期望某位英国国王的去世年龄对接下来的1或2个国王的去世年龄有某种影响，而对更远之后的国王去世年龄没有太大的影响。
快捷方式：auto.arima() 函数


auto.arima() 函数可以用来发现合适的ARIMA模型，例如输入 “library(forecast)”, 然后 “auto.arima(kings)”. 那么输出说明合适的模型是ARIMA(0,1,1). 既然对于英国国王去世年龄的时间序列，ARIMA(0,1)被认为是最合适的模型，那么原始的时间序列可以使用ARIMA(0,1,1) (p=0,d=1,q=1，这里d是差分阶层所需要的)来建模。
北半球的火山灰覆盖实例


让我们看一个另外选择合适ARIMA模型的实例。文件（http://robjhyndman.com/tsdldata/annual/dvi.dat）包含1500-1969年在北半球火山灰覆盖指数数据（从Mcleod和Hipel得到的原始数据，1994）。这是对火山爆发所散发出来的灰尘和喷雾对环境造成影响的量化度量。我们可以将其读入R并作出时间曲线图，代码如下：
volcanodust <- scan("http://robjhyndman.com/tsdldata/annual/dvi.dat", skip=1)
volcanodustseries <- ts(volcanodust,start=c(1500))
plot.ts(volcanodustseries)




# 从图上看出，随着时间增加，时间序列上面的随机波动逐渐趋与一个常数，所以添加一个合适的模型可以很好地描述这个时间序列。
# 进一步地，此时间序列看起来在平均值和方差上面是平稳的，即随着时间变化，他们的水平和方差大致趋于常量。因此，我们不需要做差分来适应ARIMA模型，而是用原始数据就可以找到合适的ARIMA模型（序列进行差分还是需要的，d为0）。
# 我们现在可以画出滞后1-20阶（lags 1-20）的自相关图和偏相关图来观察我们需要使用哪个ARIMA模型。
acf(volcanodustseries,lag.max=20) # plot a correlogram




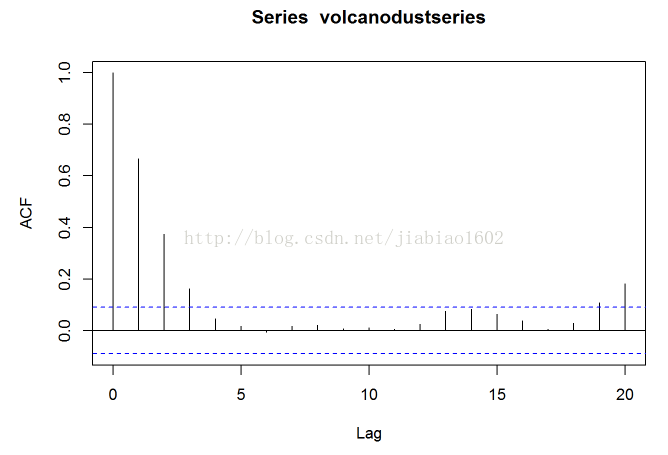
acf(volcanodustseries,lag.max=20,plot=FALSE) # get the values of the autocorrelations
## 
## Autocorrelations of series 'volcanodustseries', by lag
## 
##      0      1      2      3      4      5      6      7      8      9 
##  1.000  0.666  0.374  0.162  0.046  0.017 -0.007  0.016  0.021  0.006 
##     10     11     12     13     14     15     16     17     18     19 
##  0.010  0.004  0.024  0.075  0.082  0.064  0.039  0.005  0.028  0.108 
##     20 
##  0.182
# 我们从相关图可以看到，自相关系数在滞后1,2和3阶（lags 1,2,3） 时超出了置信边界，且自相关值在滞后3阶（lag 3）之后缩小至0. 自相关值在滞后1,2,3阶（lags 1,2,3）上是正值, 且随着滞后阶数的增加而在水平上逐渐减少(lag 1: 0.666, lag 2: 0.374, lag 3: 0.162)。
# 自相关值在滞后19和20阶（lags 19,20）上也超出了显著（置信）边界，但既然它们刚刚超出置信边界（特别是lag19），那么很可能属于偶然出现的，而自相关值在滞后4-18阶（lags 4-18）上都没有超出显著边界，而且我们可以期望1到20之间的会偶尔超出95%的置信边界。
pacf(volcanodustseries,lag.max=20)




pacf(volcanodustseries,lag.max=20,plot=FALSE)
## 
## Partial autocorrelations of series 'volcanodustseries', by lag
## 
##      1      2      3      4      5      6      7      8      9     10 
##  0.666 -0.126 -0.064 -0.005  0.040 -0.039  0.058 -0.016 -0.025  0.028 
##     11     12     13     14     15     16     17     18     19     20 
## -0.008  0.036  0.082 -0.025 -0.014  0.008 -0.025  0.073  0.131  0.063
# 从偏自相关图中我们看出在滞后1阶（lag 1）上偏自相关值(0.666)为正且超出了显著边界, 而在滞后2阶（lag 2）上面偏自相关值(-0.126)是负的且也同样超出了置信边界。偏自相关值在滞后2阶（lag 2）之后缩小至0. 既然自相关图在滞后3阶（lag 3）之后缩小为0，且偏相关图在滞后2阶（lag 2）之后缩小为0，那么下面的ARMA模型可能适合此时间序列：
## ARMA(2,0) 模型，既然偏自相关图在滞后2阶（lag 2）之后缩小至0，且自相关图在滞后3阶（lag 3）之后缩小至0，且偏相关图在滞后2阶（lag 2）之后为0. 
## ARMA(0,3) 模型，既然自相关图在滞后3阶（lag 3）之后为0，且偏相关缩小至0 (尽管这点对于此模型不太合适) 
## ARMA(p,q) 混合模型， 既然自相关图和偏相关图都缩小至0 (尽管自相关图缩小太突然对这个模型不太合适) 
Shortcut: the auto.arima() function快捷方式：auto.arima()函数


同样，我们可以使用auto.arima()来寻找合适的模型，通过输入“auto.arima(volcanodust)”, 给出ARIMA(1,0,2), 这里含有3个参数. 但是, 可以使用不同的标准来选择合适的模型（参见 auto.arima()的帮助页 面）。如果你使用 “bic” 标准, 这里对参数个数要求非常严格, 我们可以得到ARIMA(2,0,0), 即ARMA(2,0): “auto.arima(volcanodust,ic=”bic”)”
ARMA(2,0) 模型有2个参数， ARMA(0,3) 模型有3 个参数，而ARMA(p,q) 模型有至少2个参数。因此，使用简单的原则， ARMA(2,0) 模型和ARMA(p,q) 模型在这里是同样优先的选择模型。
ARMA(2,0)是2阶的自回归模型，或者称作RA(2)模型。此模型可以写作： X_t - mu = (Beta1 * (X_t-1 - mu)) + (Beta2 * (Xt-2 - mu)) + Z_t, 其中X_t 是我们学习的平稳时间序列（火山灰覆盖指数的时间序列），mu 是时间序列 X_t的平均值, Beta1 和Beta2 是估计的参数, Z_t 是平均值为0且方差为常数的白噪音。
AR (autoregressive) 模型通常被用来建立一个时间序列模型，此序列在邻项观测值上具有长期相关性。直观地，AR 模型可以用描述火山灰覆盖指数的时间序列来很好地理解，如我们可以期望在某一年的火山灰水平将会影响到后面的很多年，既然火山灰并不可能会迅速的消失。
如果ARMA(2,0) 模型(with p=2, q=0) 被用于建模火山灰覆盖指数的时间序列，它也将意味着ARIMA(2,0,0) 模型也可以使用。(with p=2, d=0, q=0, 其中d是差分的阶数). 类似地，如果ARMA(p,q) 混合模型可以使用， 其中p和q的值均大于0, 那么ARIMA(p,0,q) 模型也可以使用。
使用ARIMA模型进行预测


使用ARIMA模型进行预测 一旦你为你的时间序列数据选择了最好的ARIMA(p,d,q) 模型，你可以估计ARIMA模型的参数，并使用它们做出预测模型来对你时间序列中的未来值作预测。
你可以使用R中的“arima()”函数来估计ARIMA(p,d,q)模型中的参数。 #### 英国国王去世年龄的例子
例如，我们上面讨论的ARIMA(0,1,1) 模型看起来对英国国王去世年龄的时间序列是非常合适的模型。你可以使用R中的“arima()”函数的“order”参数来确定ARIMA模型中的p,d,q值。为了对这个时间序列(它存放在 “kingstimeseries”变量中, 见上)使用合适的ARIMA(p,d,q) 模型, 我们输入：
kingstimeseriesarima<-arima(kingstimeseries,order=c(0,1,1)) #fit an ARIMA(0,1,1) model
kingstimeseriesarima
## Series: kingstimeseries 
## ARIMA(0,1,1)                    
## 
## Coefficients:
##           ma1
##       -0.7218
## s.e.   0.1208
## 
## sigma^2 estimated as 230.4:  log likelihood=-170.06
## AIC=344.13   AICc=344.44   BIC=347.56
# 上面提到，如果我们对时间序列使用ARIMA(0,1,1)模型，那就意味着我们对一阶时间序列使用了ARMA(0,1) 模型。 ARMA(0,1) 模型可以写作X_t - mu = Z_t - (theta * Z_t-1)，其中theta是被估计的参数。 从R 中“arima()”函数的输入（上面），在国王去世年龄的时间序列中使用ARIMA(0,1,1) 模型的情况下，theta 的估计值(在R输出中以‘ma1’给出) 为-0.7218。
指定预测区间的置信水平


你可以使用forecast.Arima() 中“level”参数来确定预测区间的置信水平。例如，为了得到99.5%的预测区间，我们输入： “forecast.Arima(kingstimeseriesarima, h=5, level=c(99.5))”.
然后我们可以使用ARIMA模型来预测时间序列未来的值，使用R中forecast包的“forecast.Arima()” 函数。例如，为了预测接下来5个英国国王的去世年龄，我们输入：
library(forecast)
kingstimeseriesforecasts<-forecast.Arima(kingstimeseriesarima,h=5)
kingstimeseriesforecasts
##    Point Forecast    Lo 80    Hi 80    Lo 95     Hi 95
## 43       67.75063 48.29647 87.20479 37.99806  97.50319
## 44       67.75063 47.55748 87.94377 36.86788  98.63338
## 45       67.75063 46.84460 88.65665 35.77762  99.72363
## 46       67.75063 46.15524 89.34601 34.72333 100.77792
## 47       67.75063 45.48722 90.01404 33.70168 101.79958
# 原始时间序列中包括42位英国国王的去世年龄。forecast.Arima()函数给出接下去5个国王(国王43-47)去世年龄的预测，对于这些预测的预测区间我们同时设置为80%和95% 。第42位英国国王的去世年龄是56岁(在我们时间序列中的最后一位观察值),，ARIMA模型给出接下来5位国王的预测去世年龄为67.8岁。
# 我们可以画出42位国王去世年龄的观察值，同样画出使用ARIMA(0,1,1)模型得到的42位国王的预测去世年龄和接下去5位国王的预测值，输入：
plot.forecast(kingstimeseriesforecasts)




# 在指数平滑模型下，观察ARIMA模型的预测误差是否是平均值为0且方差为常数的正态分布（服从零均值、方差不变的正态分布）是个好主意，同时也要观察连续预测误差是否（自）相关。
# 例如，我们可以对国王去世年龄使用ARIMA(0,1,1)模型后所产生的预测误差做（自）相关图，做LjungLjungLjungLjungLjung-BoxBoxBox检 验， 输入：
acf(kingstimeseriesforecasts$residuals,lag.max=20)




Box.test(kingstimeseriesforecasts$residuals,lag=20,type="Ljung-Box")
## 
##  Box-Ljung test
## 
## data:  kingstimeseriesforecasts$residuals
## X-squared = 13.5844, df = 20, p-value = 0.8509
# 既然相关图显示出在滞后1-20阶（lags 1-20）中样本自相关值都没有超出显著（置信）边界，而且Ljung-Box检验的p值为0.9，所以我们推断在滞后1-20阶（lags 1-20）中没有明显证据说明预测误差是非零自相关的。
# 为了调查预测误差是否是平均值为零且方差为常数的正态分布（服从零均值、方差不变的正态分布），我们可以做预测误差的时间曲线图和直方图（具有正态分布曲线）：
plot.ts(kingstimeseriesforecasts$residuals) # make time plot of forecast errors




plotForecastErrors(kingstimeseriesforecasts$residuals)  # make a histogram




# 示例（中的）预测中的时间曲线图显示出对着时间增加，方差大致为常数（大致不变）（尽管下半部分的时间序列方差看起来稍微高一些）。时间序列的直方图显示预测误大致是正态分布的且平均值接近于0（服从零均值的正态分布的）。因此，把预测误差看作平均值为0方差为常数正态分布（服从零均值、方差不变的正态分布）是合理的。
# 既然依次连续的预测误差看起来不是相关，而且看起来是平均值为0方差为常数的正态分布（服从零均值、方差不变的正态分布），那么对于英国国王去世年龄的数据，ARIMA(0,1,1)看起来是可以提供非常合适预测的模型。
北半球的火山灰覆盖问题


# 我们上面讨论了，处理火山灰覆盖的时间序列数据最合适的模型可能就是ARIMA(2,0,0)。为了使用ARIMA(2,0,0)来处理这个时间序列，我们输入：
volcanodustseriesarima<-arima(volcanodustseries,order=c(2,0,0))
volcanodustseriesarima
## Series: volcanodustseries 
## ARIMA(2,0,0) with non-zero mean 
## 
## Coefficients:
##          ar1      ar2  intercept
##       0.7533  -0.1268    57.5274
## s.e.  0.0457   0.0458     8.5958
## 
## sigma^2 estimated as 4870:  log likelihood=-2662.54
## AIC=5333.09   AICc=5333.17   BIC=5349.7
# 如上所述，ARIMA(2,0,0)模型可以写作： X_t - mu = (Beta1 * (X_t-1 - mu)) + (Beta2 * (Xt-2 - mu)) + Z_t,，这里Beta1和Beta2是估计参数。arima()函数的输出告诉我们这里Betal和Beta2估计值为 0.7533和-0.1268(由arima()输出中的ar1和ar2分别给出)。 
# 现在我们要使用ARIMA(2,0,0) 模型， 我们可以用“forecast.ARIMA()” 模型来预测火山灰覆盖的未来。原始数据包含了1500至1969年间的数据。为了预测1970年至2000年的数据，我们输入：
volcanodustseriesforecasts<-forecast.Arima(volcanodustseriesarima,h=31)
volcanodustseriesforecasts
##      Point Forecast     Lo 80    Hi 80     Lo 95    Hi 95
## 1970       21.48131 -67.94860 110.9112 -115.2899 158.2526
## 1971       37.66419 -74.30305 149.6314 -133.5749 208.9033
## 1972       47.13261 -71.57070 165.8359 -134.4084 228.6737
## 1973       52.21432 -68.35951 172.7881 -132.1874 236.6161
## 1974       54.84241 -66.22681 175.9116 -130.3170 240.0018
## 1975       56.17814 -65.01872 177.3750 -129.1765 241.5327
## 1976       56.85128 -64.37798 178.0805 -128.5529 242.2554
## 1977       57.18907 -64.04834 178.4265 -128.2276 242.6057
## 1978       57.35822 -63.88124 178.5977 -128.0615 242.7780
## 1979       57.44283 -63.79714 178.6828 -127.9777 242.8634
## 1980       57.48513 -63.75497 178.7252 -127.9356 242.9059
## 1981       57.50627 -63.73386 178.7464 -127.9145 242.9271
## 1982       57.51684 -63.72330 178.7570 -127.9040 242.9376
## 1983       57.52212 -63.71802 178.7623 -127.8987 242.9429
## 1984       57.52476 -63.71538 178.7649 -127.8960 242.9456
## 1985       57.52607 -63.71407 178.7662 -127.8947 242.9469
## 1986       57.52673 -63.71341 178.7669 -127.8941 242.9475
## 1987       57.52706 -63.71308 178.7672 -127.8937 242.9479
## 1988       57.52723 -63.71291 178.7674 -127.8936 242.9480
## 1989       57.52731 -63.71283 178.7674 -127.8935 242.9481
## 1990       57.52735 -63.71279 178.7675 -127.8934 242.9481
## 1991       57.52737 -63.71277 178.7675 -127.8934 242.9482
## 1992       57.52738 -63.71276 178.7675 -127.8934 242.9482
## 1993       57.52739 -63.71275 178.7675 -127.8934 242.9482
## 1994       57.52739 -63.71275 178.7675 -127.8934 242.9482
## 1995       57.52739 -63.71275 178.7675 -127.8934 242.9482
## 1996       57.52739 -63.71275 178.7675 -127.8934 242.9482
## 1997       57.52739 -63.71275 178.7675 -127.8934 242.9482
## 1998       57.52739 -63.71275 178.7675 -127.8934 242.9482
## 1999       57.52739 -63.71275 178.7675 -127.8934 242.9482
## 2000       57.52739 -63.71275 178.7675 -127.8934 242.9482
# 我们可以画出原始时间序列和预测数值，输入：
plot(volcanodustseriesforecasts)




# 一个棘手的问题这个模型预测中火山灰覆盖数据有负值，但是这个值只有正值才有意义。出现负值的原因是arima()和forecast.Arima()函数并不知道这个数值必须是正的。明显地，我们现在的预测模型中有并不令人满意的一面。
# 我们应该再次观察预测误差是否相关，且他们是否是平均值为0方差为常数的正态分布（服从零均值、方差不变的正态分布）。为了检测相邻预测误差之间的相关性，我们做出相关图并使用Ljung-Box检验：
acf(volcanodustseriesforecasts$residuals,lag.max=20)




Box.test(volcanodustseriesforecasts$residuals,lag=20,type="Ljung-Box")
## 
##  Box-Ljung test
## 
## data:  volcanodustseriesforecasts$residuals
## X-squared = 24.3642, df = 20, p-value = 0.2268
# 相关图显示出示例在滞后20阶（lag 20）自相关值超出了显著（置信）边界。但是，这很可能是偶然的，既然我们认为1/20的样本自相关值是可以超出95%显著边界的。另外，Ljung-Box检验的p值为0.2，表明没有证据证明在滞后1-20阶（lags 1-20）中预测误差是非零自相关的。 
# 为了检查预测误差是否是平均值为0且方差为常数的正态分布，我们做一个预测误差的时间曲线图和一个直方图：
plot.ts(volcanodustseriesforecasts$residuals) # make time plot of forecast errors




plotForecastErrors(volcanodustseriesforecasts$residuals) # make a histogram




# 预测误差的时间曲线图显示随着时间推移预测误差的方差大致是常数，但是，预测误差的时间序列看起来有一个负值，而不是0. 通过计算预测误差的平均我们可以确定其值为-0.22.
mean(volcanodustseriesforecasts$residuals)
## [1] -0.2205417
# 预测误差的直方图（上图）显示尽管预测误差的平均值为负，与正态分布相比，预测误差的分布是向左偏移的。因此，我们推断说它是平均值为0且方差为常数的正态分布是不太准确的。因此，ARIMA(2,0,0)很可能对火山灰覆盖时间序列数据来说并非是最好的模型，显然它是可以被优化的