李宏毅机器学习课程10~~~卷积神经网络

---

卷积的意义

---

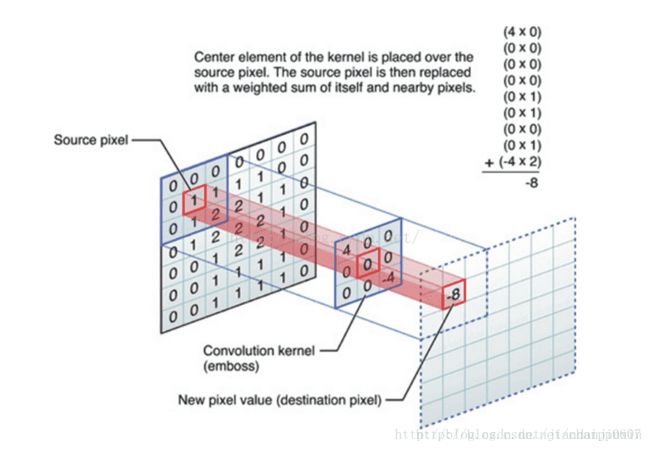
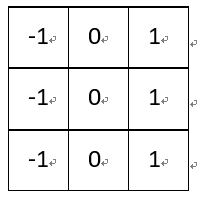
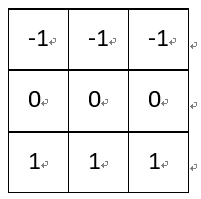
数字图像是一个二维的离散信号，对数字图像做卷积操作其实就是利用卷积核（卷积模板）在图像上滑动，将图像点上的像素灰度值与对应的卷积核上的数值相乘，然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值，并最终滑动完所有图像的过程。

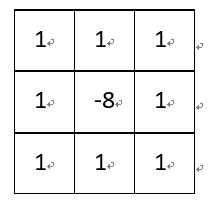
这张图可以清晰的表征出整个卷积过程中一次相乘后相加的结果：该图片选用3*3的卷积核，卷积核内共有九个数值，所以图片右上角公式中一共有九行，而每一行都是图像像素值与卷积核上数值相乘，最终结果-8代替了原图像中对应位置处的1。这样沿着图片一步长为1滑动，每一个滑动后都一次相乘再相加的工作，我们就可以得到最终的输出结果。除此之外，卷积核的选择有一些规则：

1）卷积核的大小一般是奇数，这样的话它是按照中间的像素点中心对称的，所以卷积核一般都是3x3，5x5或者7x7。有中心了，也有了半径的称呼，例如5x5大小的核的半径就是2。
2）卷积核所有的元素之和一般要等于1，这是为了原始图像的能量（亮度）守恒。其实也有卷积核元素相加不为1的情况，下面就会说到。

3）如果滤波器矩阵所有元素之和大于1，那么滤波后的图像就会比原图像更亮，反之，如果小于1，那么得到的图像就会变暗。如果和为0，图像不会变黑，但也会非常暗。

4）对于滤波后的结构，可能会出现负数或者大于255的数值。对这种情况，我们将他们直接截断到0和255之间即可。对于负数，也可以取绝对值。

卷积操作有两个问题：
1. 图像越来越小；
2. 图像边界信息丢失，即有些图像角落和边界的信息发挥作用较少。因此需要padding。

卷积核大小通常为奇数，
一方面是为了方便same卷积padding对称填充，左右两边对称补零；
n+2p-f+1=n
p=(f-1)/2
另一方面，奇数过滤器有中心像素，便于确定过滤器的位置。

更多细节见
理解图像卷积操作的意义
padding

输入：n*c0*w0*h0
输出：n*c1*w1*h1
其中，c1就是参数中的num_output，生成的特征图个数
 w1=floor((w0+2*pad-kernel_size)/stride)+1;向下取整
 h1=floor((h0+2*pad-kernel_size)/stride)+1;向下取整
如果设置stride为1，前后两次卷积部分存在重叠。如果设置pad=(kernel_size-1)/2,则运算后，宽度和高度不变。
由pad, kernel_size和stride三者共同决定。

更多细节可见卷积步长

不同卷积核下卷积意义

我们经常能看到的，平滑，模糊，去燥，锐化，边缘提取等等工作，其实都可以通过卷积操作来完成，下面我们一一举例说明一下：
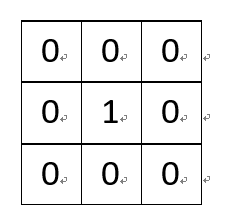
（1）一个没有任何作用的卷积核：

将原像素中间像素值乘1，其余全部乘0，显然像素值不会发生任何变化。
（2）平滑均值滤波：
选择卷积核：

该卷积核的作用在于取九个值的平均值代替中间像素值，所以起到的平滑的效果：

（3）高斯平滑：
卷积核：

高斯平滑水平和垂直方向呈现高斯分布，更突出了中心点在像素平滑后的权重，相比于均值滤波而言，有着更好的平滑效果。

（4）图像锐化：
卷积核：

该卷积利用的其实是图像中的边缘信息有着比周围像素更高的对比度，而经过卷积之后进一步增强了这种对比度，从而使图像显得棱角分明、画面清晰，起到锐化图像的效果。

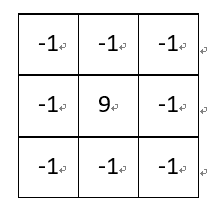
除了上述卷积核，边缘锐化还可以选择：

（5）梯度Prewitt：
水平梯度：

垂直梯度：

梯度Prewitt卷积核与Soble卷积核的选定是类似的，都是对水平边缘或垂直边缘有比较好的检测效果。

（6）Soble边缘检测：
Soble与上述卷积核不同之处在于，Soble更强调了和边缘相邻的像素点对边缘的影响。
水平梯度：

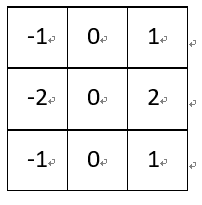
垂直梯度：

以上的水平边缘与垂直边缘检测问题可以参考：Soble算子水平和垂直方向导数问题

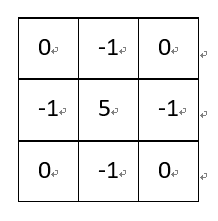
（7）梯度Laplacian：

卷积核：

Laplacian也是一种锐化方法，同时也可以做边缘检测，而且边缘检测的应用中并不局限于水平方向或垂直方向，这是Laplacian与soble的区别。下面这张图可以很好的表征出二者的区别：来源于OpenCV官方文档

代码实现

可以利用OpenCV提供的filter2D函数完成对图像进行卷积操作，其函数接口为：

CV_EXPORTS_W void filter2D(
InputArray src, 
OutputArray dst, 
int ddepth,
InputArray kernel, 
Point anchor=Point(-1,-1),
double delta=0, 
int borderType=BORDER_DEFAULT );

第一个参数: 输入图像
第二个参数: 输出图像，和输入图像具有相同的尺寸和通道数量
第三个参数: 目标图像深度，输入值为-1时，目标图像和原图像深度保持一致。
第四个参数: 卷积核，是一个矩阵
第五个参数：内核的基准点(anchor)，其默认值为(-1,-1)说明位于kernel的中心位置。基准点即kernel中与进行处理的像素点重合的点。
第五个参数: 在储存目标图像前可选的添加到像素的值，默认值为0
第六个参数: 像素向外逼近的方法，默认值是BORDER_DEFAULT。

#include 
#include 
#include 
#include 
#include 
using namespace std;
using namespace  cv;

int main()
{
    Mat srcImage = imread("1.jpg");
    namedWindow("srcImage", WINDOW_AUTOSIZE);
    imshow("原图", srcImage);
    Mat kernel = (Mat_<double>(3,3) << 
        -1, 0 ,1,
        -2, 0, 2,
        -1, 0, 1);
    Mat dstImage;
    filter2D(srcImage,dstImage,srcImage.depth(),kernel);
    namedWindow("dstImage",WINDOW_AUTOSIZE);
    imshow("卷积图",dstImage);
    waitKey(0);
    return 0;
}

所以代码的实现就非常简单了，不同的卷积操作只需要改变卷积核kernel 即可。

更多细节见
理解图像卷积操作的意义

TensorFlow基本操作 实现卷积和池化

---

A Beginner’s Guide To Understanding Convolutional Neural Networks

---

卷积的可视化图

---

A guide to convolution arithmetic for deep learning

A guide to convolution arithmetic for deep learning-github

---

原来，动物的眼睛看世界都是自带滤镜的！
看问题的角度不一样，导致图像识别的任务就不一样。

---

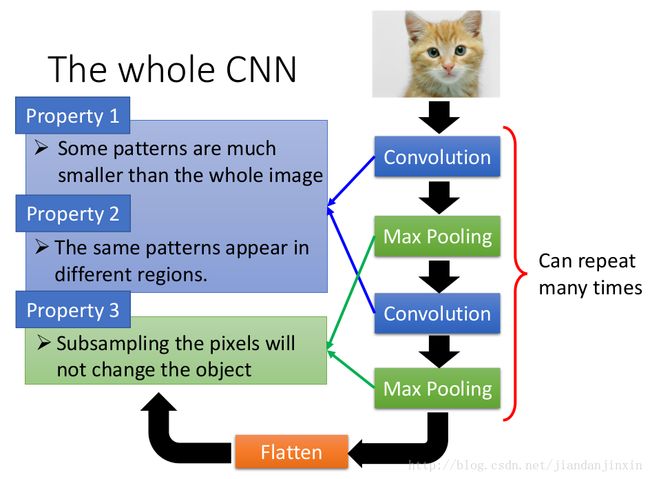
Why CNN for Image-motivation

---

CNN的动机就是减少参数。CNN相当于Fully Connected Network简化版本. CNN的Function set 的Space 比较小，而Fully Connected Network的Function set 的Space 比较大。

pattern 往往小于图片，因此neuron没有必要discover整副图片

同样的pattern可能出现到图片中不同的位置

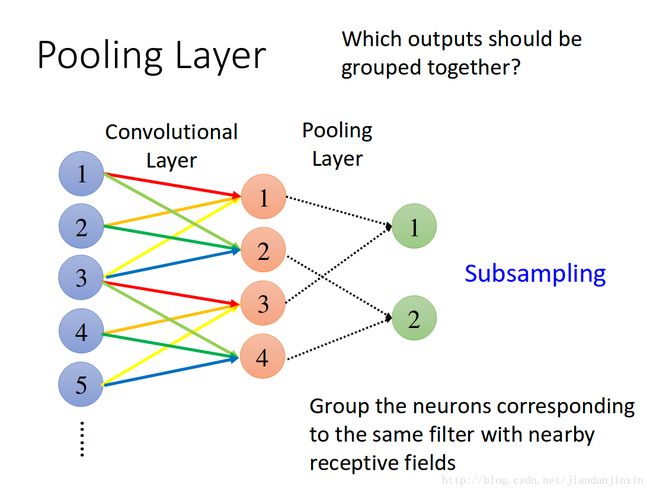
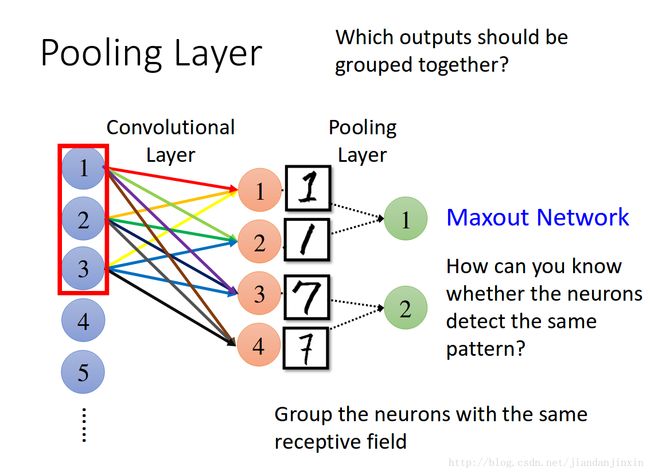
下采样不会影响图片辨识的结果

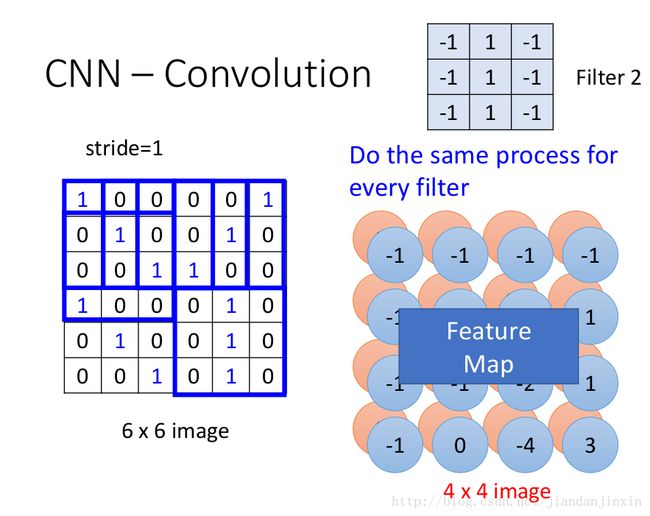
Convolution考虑Property1 和Property2,Pooling考虑的是Property3.

convolution卷积　也称为核，滤波器，Feature Detection.

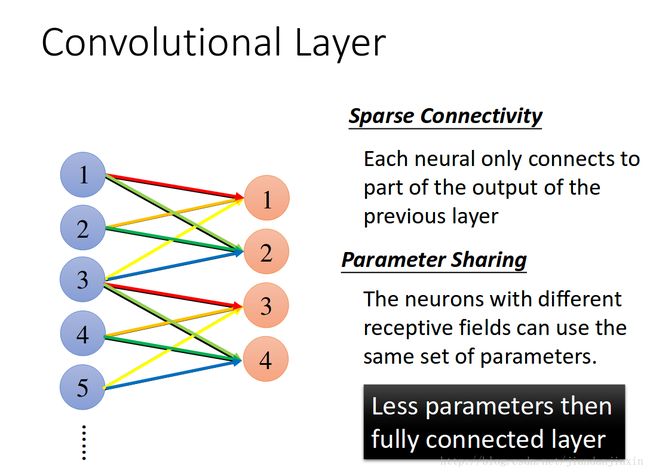
卷积层两个主要优势：共享参数和稀疏连接。

共享参数

稀疏连接

卷积神经网络有一定的平移不变性属性

例如平移图像中的猫，依然可以检测到平移后的猫，这是因为局部连接，猫的特征在同一副图的任何位置都可被检测出来，只要这个滤波器检测到猫的特征，那么不论猫在图像中的任何位置都是可以被检测出来的。

CNN具有一定的平移、旋转和缩放不变性

CNN 的平移不变性的一个重要来源就是池化（Pooling）操作。
池化可以提供一定的平移、旋转不变性。maxpool能保证在在一定范围内平移特征能得到同样的激励，也就是说最大池化操作会提取出相同的值而不管你是否有一定程度内的平移或旋转。CNN具有一定的旋转缩放不变性，见How is a convolutional neural network able to learn invariant features?但是这个旋转不变性是有一定的角度控制的，当然起作用的是maxpooling 层，当我们正面拍一些照片的时候，也许我们学习得到的一些地方的activation会比较大，当我们略微的转过一点角度之后，由于maxpooling的存在，会使得我们的maxpooling依然在那个地方取到最大值，所以有一定的旋转不变性。但是，对于角度很大的来说，maxpooling可能也会失效，所以需要一定的data augmentation，或者你也可以提高maxpooling的窗口，来提高一定的旋转不变性。。所以说maxpooling的窗口越大可以旋转保持抽取特征不变性的角度就越大。现在很多人解决这种问题的方法都是用data augmentation。

data augmentation:人工增加训练集的大小. 通过平移, 翻转, 加噪声等方法从已有数据中创造出一批”新”的数据

权值共享还赋予了卷积网络对平移的容忍性，而池化层降采样则进一步降低了输出参数量，同时赋予模型对轻度变形的容忍性，提高了模型的泛化能力。

为何使用卷积？

pool层的组合方式

各种好基本网络结构组合的方式

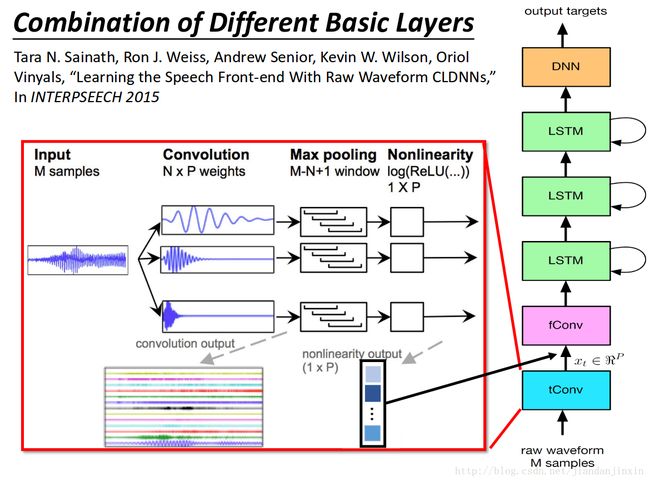
http://speech.ee.ntu.edu.tw/~tlkagk/courses/MLDS_2017/Lecture/Basic%20Structure%20(v8).pdf

权值共享这个词说全了就是整张图片在使用同一个卷积核内的参数，比如一个3*3*1的卷积核，这个卷积核内9个的参数被整张图共享，而不会因为图像内位置的不同而改变卷积核内的权系数。说的再直白一些，就是用一个卷积核不改变其内权系数的情况下卷积处理整张图片。

！LeNet首次把卷积的思想加入到神经网络模型中，这是一项开创性的工作，而在此之前，神经网络输入的都是提取到的特征而已，就比如想要做一个房价预测，我们选取了房屋面积，卧室个数等等数据作为特征。而将卷积核引入到了神经网络去处理图片后，自然而然就会出现一个问题，神经网络的输入是什么？如果还是一个个像素点上的像素值的话，那就意味着每一个像素值都会对应一个权系数，这样就带来了两个问题：
1.每一层都会有大量的参数
2.将像素值作为输入特征本质上和传统的神经网络没有区别，并没有利用到图像空间上的局部相关性。

而权值共享的卷积操作有效解决了这个问题，无论图像的尺寸是多大，都可以选择固定尺寸的卷积核，LeNet中最大的卷积核只有5*5*1，而在AlexNet中最大的卷积核也不过是11*11*3。而卷积操作保证了每一个像素都有一个权系数，只是这些系数是被整个图片共享的，着大大减少了卷积核中的参数量。此外卷积操作利用了图片空间上的局部相关性，这也就是CNN与传统神经网络或机器学习的一个最大的不同点，特征的自动提取。

这也就是为什么卷积层往往会有多个卷积核（甚至几十个，上百个），因为权值共享后意味着每一个卷积核只能提取到一种特征，为了增加CNN的表达能力，当然需要多个核，不幸的是，它是一个Hyper-Parameter。
更多细节见
如何理解卷积神经网络中的权值共享

卷积层在CNN中扮演着很重要的角色——特征的抽象和提取。

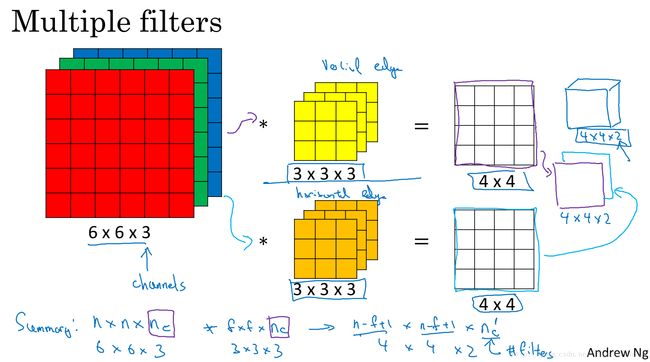
在CNN中，卷积核的尺寸是人为指定的，但是卷积核内的数全部都是需要不断学习得到的。比如一个卷积核的尺寸为3*3*3，分别是宽，高和厚度，那么这一个卷积核中的参数有27个。

在这里需要说明一点：
卷积核的厚度=被卷积的图像的通道数
卷积核的个数=卷积操作后输出的通道数

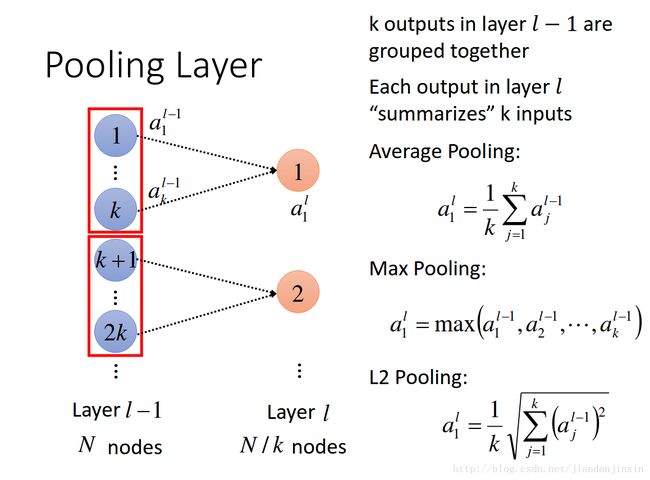
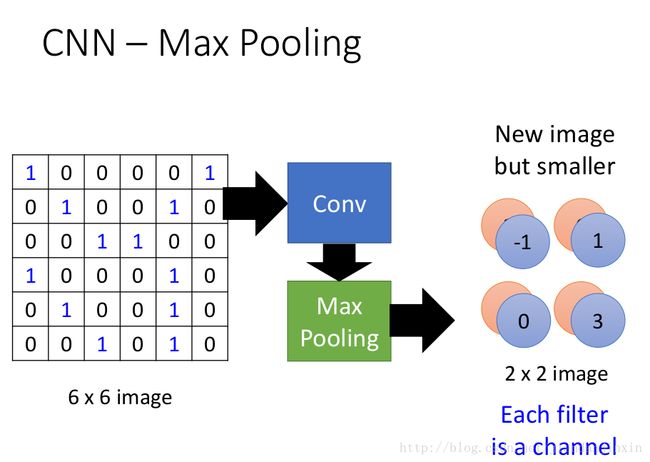
池化操作（Pooling）用于卷积操作之后，其作用在于特征融合和降维，其实也是一种类似卷积的操作，只是池化层的所有参数都是超参数，都是不用学习得到的。

上面这张图解释了最大池化（Max Pooling）的操作过程，核的尺寸为2*2，步长为2，最大池化的过程是将2*2尺寸内的所有像素值取最大值，作为输出通道的像素值。
除了最大池化外，还有平均池化（Average Pooling），也就是将取最大改为取平均。
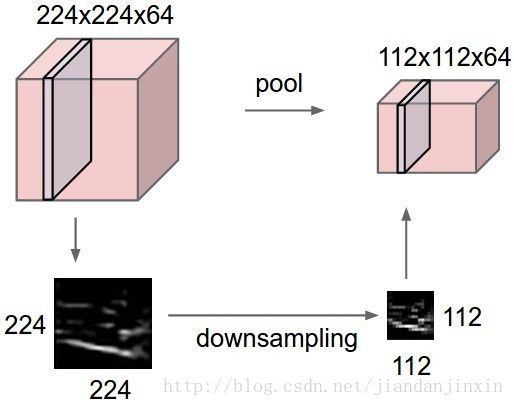
一个输入为224*224*64的图像，经过最大池化后的尺寸变为112*112*64，可以看到池化操作的降维改变的是图像的宽高，而不改变通道数。

---

设计CNN

---

3X3意味着用3X3可以catch 到这个pattern－－－Property 1

Pattern Size <= 3X3

3X3 filter的设计使得pattern响应最大的设计为好。—-Property 2

同样的pattern，filter都会使得其响应最大，所以在不同位置pattern 都可以使用同样的filter.

最大池化，平均池化，随机池化。可以同时做最大池化和平均池化。

1) mean-pooling，即对邻域内特征点只求平均，对背景保留更好；
2) max-pooling，即对邻域内特征点取最大，对纹理提取更好；
3) Stochastic-pooling，介于两者之间，通过对像素点按照数值大小赋予概率，再按照概率进行亚采样；

4) 重叠池化（Overlapping Pooling）
重叠池化的相邻池化窗口之间会有重叠区域。该部分详见 Krizhevsky, I. Sutskever, andG. Hinton, “Imagenet classification with deep convolutional neural networks”

5) 空间金字塔池化（Spatial Pyramid Pooling）
空间金字塔池化拓展了卷积神经网络的实用性，使它能够以任意尺寸的图片作为输入。该部分详见Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition，这篇paper主要的创新点在于提出了空间金字塔池化。paper主页：http://research.microsoft.com/en-us/um/people/kahe/eccv14sppnet/index.html 这个算法比R-CNN算法的速度快了n多倍。
理解见# 深度学习（十九）基于空间金字塔池化的卷积神经网络物体检测

6) ROIs Pooling
ROI pooling layer实际上是SPP-NET的一个精简版，SPP-NET对每个proposal使用了不同大小的金字塔映射，而ROI pooling layer只需要下采样到一个7x7的特征图.对于VGG16网络conv5_3有512个特征图，这样所有region proposal对应了一个7*7*512维度的特征向量作为全连接层的输入.

pooling是一种信息汇集,信息粗粒度化

SUM Pooling, AVE Pooling, MAX Pooling,MOP Pooling, CROW Pooling , RMAC Pooling

SUM pooling基于SUM pooling的中层特征表示方法，指的是针对中间层的任意一个channel（比如VGGNet16, pool5有512个channel），将该channel的feature map的所有像素值求和，这样每一个channel得到一个实数值，N个channel最终会得到一个长度为N的向量，该向量即为SUM pooling的结果。

作者：小白菜
链接：https://www.zhihu.com/question/41948919/answer/196459630

---

Max pooling的主要功能是downsamping，却不会损坏识别结果。 这意味着卷积后的Feature Map中有对于识别物体不必要的冗余信息。

最大化操作的功能是只要在任何一个象限内提取到某个特征，它都会保留在最大池化的输出里。池化层并没有参数学习，梯度下降无需改变任何值。

池化层

---

filter为何随着层数加深而越来越多，这是因为前面的层是catch 比较小的patter,后面的层是catch 比较丰富的pattern,所以需要的参数比较多，因而需要更多的filter.

有些问题不适合使用Pooling,要根据具体问题来设计CNN结构。

pooling是一种信息汇集,信息粗粒度化。Pooling实际上也可以当做一种尺度缩放，conv后面不一定要有pooling。

conv后面不一定要有pooling.像VGG结构，都会在很多个conv之后才加一个pooling. ResNet, 152层里面总共就三四个pooling. Pooling只是用来减小feature map的大小，可能其实并不是那么必要。在论文Striving for Simplicity: The All Convolutional Net研究表明用stride大于１的conv来代替pooling效果是一样的。

---

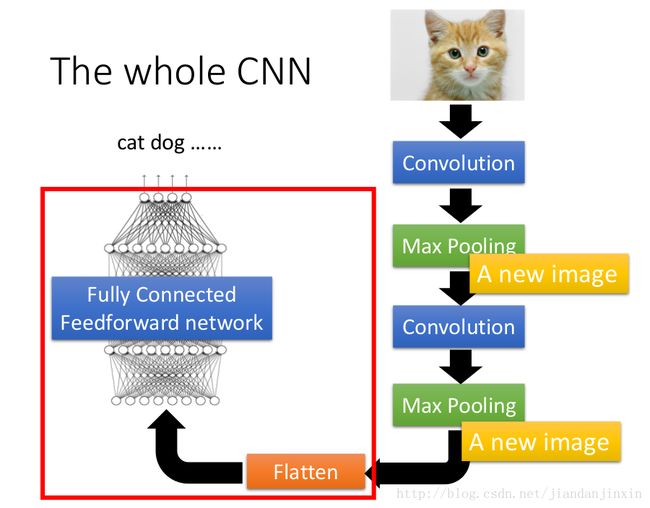
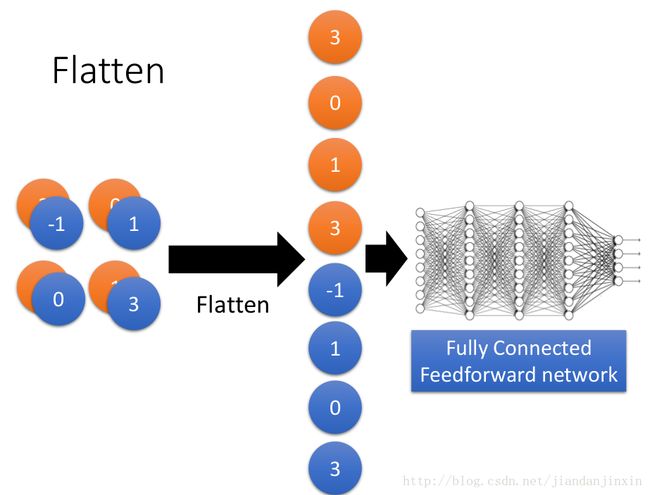
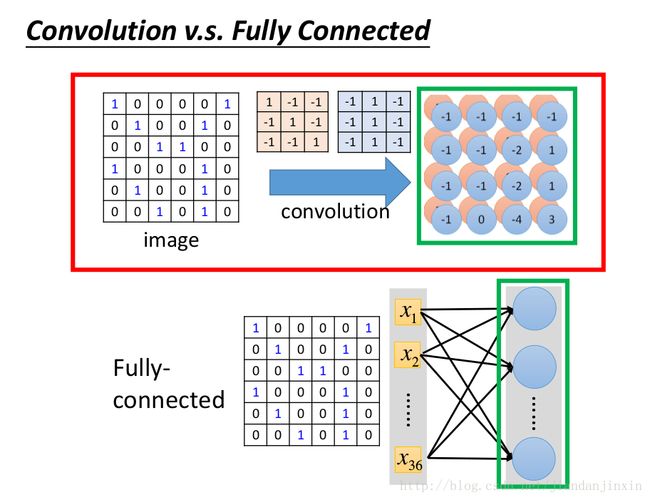
Convolution v.s. Fully Connected

---

卷积后的图像比原图小

原图中的每个patch，在卷积后的图像中都有多个位置对应。（多个filter卷积后的图），上图中每个3X3的patch，都有两个位置对应，因为使用了两个filter.

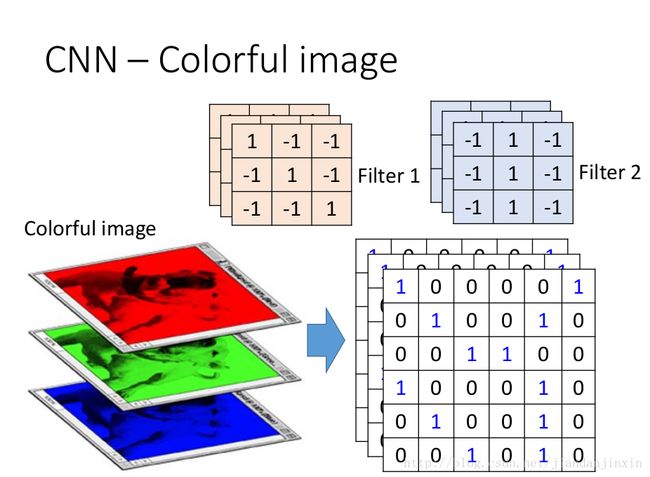
彩图中的原图中有三个通道，那么对应的每个filter也应该有三个通道，这些filter都是通过学习得到的。

---

该部分内容转自：YJango的卷积神经网络——介绍
Depth维的处理

现在我们已经知道了depth维度只有1的灰度图是如何处理的。 但前文提过，图片的普遍表达方式是下图这样有3个channels的RGB颜色模型。 当depth为复数的时候，每个feature detector是如何卷积的？

**现象：**2x2所表达的filter size中，一个2表示width维上的局部连接数，另一个2表示height维上的局部连接数，并却没有depth维上的局部连接数，是因为depth维上并非局部，而是全部连接的。

在2D卷积中，filter在张量的width维, height维上是局部连接，在depth维上是贯串全部channels的。

类比：想象在切蛋糕的时候，不管这个蛋糕有多少层，通常大家都会一刀切到底，但是在长和宽这两个维上是局部切割。

下面这张图展示了，在depth为复数时，filter是如何连接输入节点到输出节点的。 图中红、绿、蓝颜色的节点表示3个channels。 黄色节点表示一个feature detector卷积后得到的Feature Map。 其中被透明黑框圈中的12个节点会被连接到黄黑色的节点上。

    在输入depth为1时：被filter size为2x2所圈中的4个输入节点连接到1个输出节点上。
    在输入depth为3时：被filter size为2x2，但是贯串3个channels后，所圈中的12个输入节点连接到1个输出节点上。
    在输入depth为n时：2x2xn个输入节点连接到1个输出节点上。

注意：三个channels的权重并不共享。 即当深度变为3后，权重也跟着扩增到了三组，如式子(3)所示，不同channels用的是自己的权重。 式子中增加的角标r,g,b分别表示red channel, green channel, blue channel的权重。

(3)

计算例子：用x_{r0}表示red channel的编号为0的输入节点，x_{g5}表示green channel编号为5个输入节点。x_{b1}表示blue channel。如式子(4)所表达，这时的一个输出节点实际上是12个输入节点的线性组合。

每个filter会在width维, height维上，以局部连接和空间共享，并贯串整个depth维的方式得到一个Feature Map。

更多细节理解见
3D卷积

Summary of notation

---

Convolution中每个neuron仅仅连接了９个input,而不是连接所有的input.

---

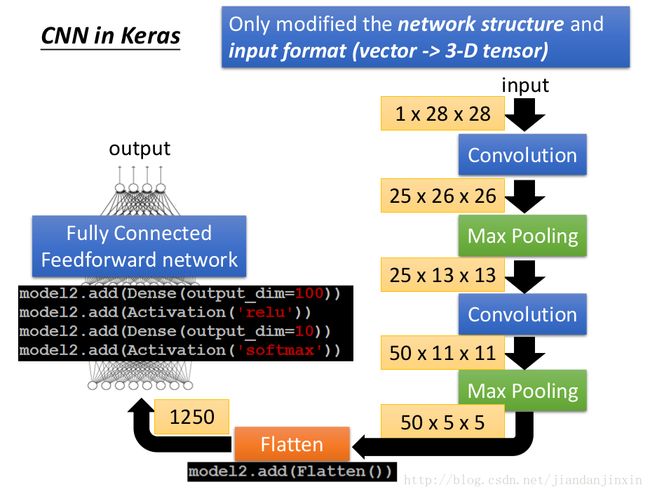
CNN in Keras

---

filter为何随着层数加深而越来越多，这是因为前面的层是catch 比较小的patter,后面的层是catch 比较丰富的pattern,所以需要的参数比较多，因而需要更多的filter.

有些问题不适合使用Pooling,要根据具体问题来设计CNN结构。

---

(5x5+1)x8=208
(5x5+1)x16=416
400x120+1=48001
120x84+1=10081

卷积核的厚度=被卷积的图像的通道数
卷积核的个数=卷积操作后输出的通道数

池化层不需要训练参数。全连接层的参数最多。卷积核的个数逐渐增多。激活层的size，逐渐减少。

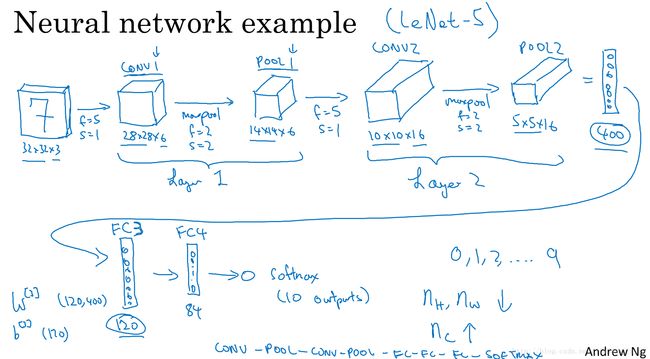
卷积神经网络示例

---

分析CNN的结果

---

1. First Convolution Layer

查看第一个layer，这是因为第一个layer通常是比较简单的可理解的layer.　而第二个layer或者后面的layer,往往不可理解，说白了就是生成了我们无法理解的东西。

2. How about higher layer?

Higher layers,通常是其他层layer的输出结果，所以管辖的范围比较大，所以查看higher layer会看到比较大的范围（前面filter的结果组合）。不同的filter对应不同的pattern.

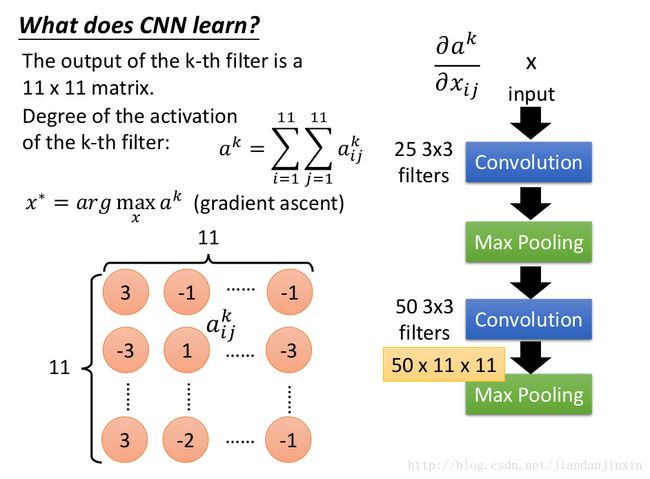
3. What does CNN learn?

找到一张图片使得某个filter响应最大。相当于filter固定，未知的是输入的图片。

对Fully connected Network做同样的分析。

同样可以对要求的未知图像做一些限制，比如加regulation项。

遮挡某个部位，来判别该部位对模型的影响。

---

Deep Dream

强化CNN所看到的东西。使得每个filter得到的结果夸张化，大的更大，小的更小。

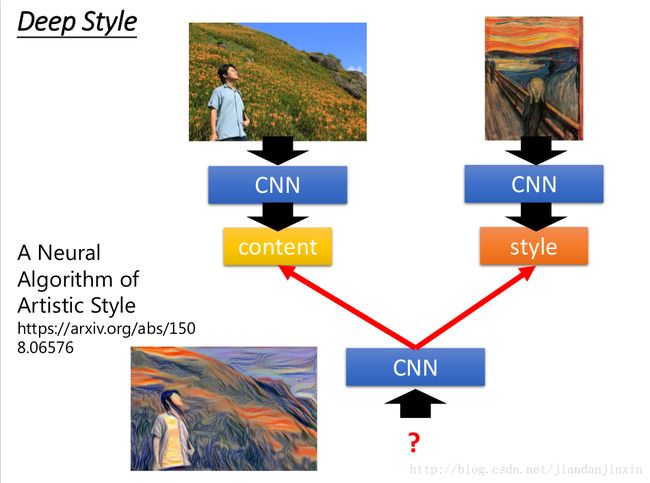
画风迁移

CNN的一些filter结果代表内容，一些filter结果代表风格。在找另外一张图片，使得一些filter结果更像内容，另外一些filter结果更像风格。

https://deepart.io/

---

DeepDream的代码实现
Understanding Deep Dreams
Inceptionism: Going Deeper into Neural Networks
Autoencoding beyond pixels using a learned similarity metric

更多解读见
瞎谈CNN：通过优化求解输入图像

---

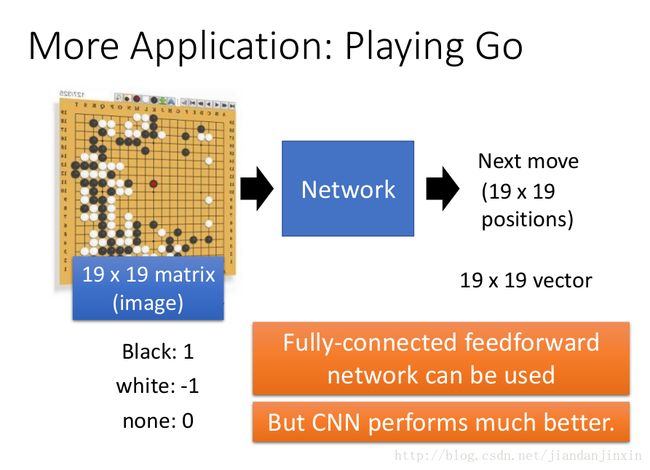
Alphago

---

---

参考文献

---

Home: http://speech.ee.ntu.edu.tw/~tlkagk/courses_ML17.html

YJango的卷积神经网络——介绍

问题

１．　Pooling 同时max, average?
2. 查看Fully Connected Network 中第一层layer,看看具体是代表的什么？
3. 多个不同核，是否可以借助手动设置呢？
4. P24里面的　50X11X11 如何得出的呢？解释见YJango的卷积神经网络——介绍