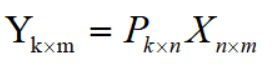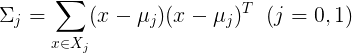ML-降维：PCA、SVD、LDA、MDS、LLE、LE算法总结

1.PCA主成分分析

PCA是不考虑样本类别输出的无监督降维技术，实现的是高维数据映射到低维的降维。

PCA原理这个介绍的不错：https://www.cnblogs.com/pinard/p/6239403.html

线性代数矩阵性质背景：特征值表示的是矩阵在特征值对应的特征向量方向上的伸缩大小；线性代数的本质这个课有不错介绍：https://www.bilibili.com/video/av6731067

步骤：

1）组成数据矩阵

def get_date():
    m_vec = np.array([0, 0, 0])
    cov_vec = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
    # 20个3维，且每个维度以m_vec为均值，以cov_vec为方差的多元正态分布随机数
    c1 = np.random.multivariate_normal(m_vec, cov_vec, 20).T

    m_vec2 = np.array([1, 1, 1])
    cov_vec2 = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
    # 20个3维，且每个维度以m_vec2为均值，以cov_vec2为方差的多元正态分布随机数
    c2 = np.random.multivariate_normal(m_vec2, cov_vec2, 20).T
    # 合并构造一个3 x 40 的数据集
    data = np.concatenate((c1, c2), axis=1)
    return data


X = get_date()

 

2） 计算特征均值

mean_X = np.mean(X, axis=1).reshape(X.shape[0], 1)

 

3） 去中心化的新数据矩阵

 

dmean_X = X - mean_X

4）计算协方差矩阵

 

m = dmean_X.shape[1]
C = np.dot(dmean_X, dmean_X.T) / m

 5）C的分解

计算C的特征值，特征向量，（大到小排列，特征值-向量一一对应）

eig_val_sc, eig_vec_sc = np.linalg.eig(C)

 6）取得投影矩阵

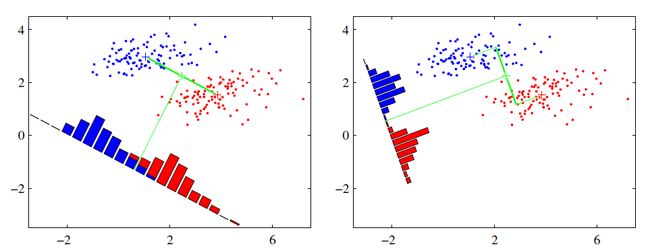
选择取C分解的前k(k

 

k=2
# 从大到小特征值的k个索引
argsort_eigv = np.argsort(eig_val_sc)[-k:][::-1]
# 从大到小特征值的k个索引对应的特征向量，构造新矩阵
W = eig_vec_sc[argsort_eigv]

 7）实现数据降维，n维到k维

# 构造的新矩阵对原数据X降维
new_X = np.dot(W, X)

然后用Yk.m替代Xn.m，作为降维数据集使用

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt


def get_date():
    m_vec = np.array([0, 0, 0])
    cov_vec = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
    # 20个3维，且每个维度以m_vec为均值，以cov_vec为方差的多元正态分布随机数
    c1 = np.random.multivariate_normal(m_vec, cov_vec, 20).T

    m_vec2 = np.array([1, 1, 1])
    cov_vec2 = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1]])
    # 20个3维，且每个维度以m_vec2为均值，以cov_vec2为方差的多元正态分布随机数
    c2 = np.random.multivariate_normal(m_vec2, cov_vec2, 20).T
    # 合并构造一个3 x 40 的数据集
    data = np.concatenate((c1, c2), axis=1)
    return data


X = get_date()

k = 2

# ====基于线性代数实现PCA降维======
mean_X = np.mean(X, axis=1).reshape(X.shape[0], 1)
dmean_X = X - mean_X
m = dmean_X.shape[1]
C = np.dot(dmean_X, dmean_X.T) / m

# 矩阵分解 奇异值，特征向量
eig_val_sc, eig_vec_sc = np.linalg.eig(C)

# 从大到小特征值的k个索引
argsort_eigv = np.argsort(eig_val_sc)[-k:][::-1]
# 从大到小特征值的k个索引对应的特征向量，构造新矩阵
W = eig_vec_sc[argsort_eigv]
# 构造的新矩阵对原数据X降维
new_X = np.dot(W, X)
# 显示降维后的数据
plt.scatter(new_X.T[:, 0], new_X.T[:, 1], c='y')

plt.show()

 可以看到降维到2的数据，还是有明显的区分的。

sklearn-PCA

decomposition.PCA(n_components=None, copy=True, whiten=False)

from sklearn.decomposition import PCA
pca = PCA(n_components=3)
pca.fit(X)
print pca.explained_variance_ratio_
print pca.explained_variance_

X_new = pca.transform(X)#实现对X的降维

n_components:  PCA算法中所要保留的主成分个数n，也即保留下来的特征个数n
copy:表示是否在运行算法时，将原始训练数据复制一份。
若为True，则运行PCA算法后，原始训练数据的值不会有任何改变，因为是在原始数据的副本上进行运算；若为False，则运行PCA算法后，原始训练数据的值会改，因为是在原始数据上进行降维计算。
whiten: bool，缺省时默认为False，True使得每个特征具有相同的方差。
explained_variance_ratio_：计算了每个特征方差贡献率，所有总和为1
explained_variance_：方差值 

可以看到，sklearn的效果和前面编程实现的一样。 

---

梯度上升PCA

前面是基于矩阵分解，这个是用梯度下降：

https://www.jianshu.com/p/1e9cab07d54d

 

---

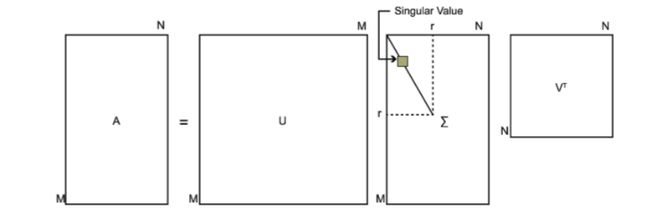
2.SVD

原理参考：https://www.cnblogs.com/pinard/p/6251584.html

这里不加证明的写出如下总结：

对于任意矩阵Amxn，其奇异值是的特征值的平方根；

的特征向量是：v1,v2,v3，则A的特征向量是：

若特征值<0，mn时需要根据已求出的特征向量计算正交，得出多个正交向量要正交化。 

 

2.1SVD降维：

通常，按大小排列的奇异值，减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：，可以实现降维。（线性代数中，特征向量意味着方向，对应的特征值意味着矩阵在特征向量上的拉伸程度，取大的k个特征值对应的特征向量，可以近似的描述这个拉伸过程，极大程度上保存原有数据形状）

sklearn实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import load_iris

# ======创建数据集========
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
labels = df.iloc[:, -1].values
data = df.iloc[:, :-1].values
samples, features = df.shape
print(samples, features)

# =======这里SVD========
U, s, V = np.linalg.svd(data)

# =====取前3维数据显示===========
newdata = U[:, :3]
fig = plt.figure()
ax = Axes3D(fig)

# =======每个类型的形状和颜色=====
marks = ['o', '*', '+']
colors = ['r', 'b', 'g']
for i in range(samples):
    ax.scatter(newdata[i, 0], newdata[i, 1], newdata[i, 2], c=colors[int(labels[i])], marker=marks[int(labels[i])])

plt.show()

 

---

3 LDA

LDA是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。核心思想是投影后类内方差最小，类间方差最大，如下右图（2维到1维），显然比左图更符合这个思想，LDA就是希望降维后的数据，能最大化的满足这个。

原理介绍：https://www.cnblogs.com/pinard/p/6244265.html

考虑二类别情况：

定义均值向量：

协方差：

希望同类更近，异类更远，意味着希望如下关系尽可能大：

定义类内散度矩阵：

类间散度矩阵：

目标变成了：

对上目标进行求解，其实是转为对某矩阵的分解，我的另一个文章的最后一张图有介绍：https://blog.csdn.net/jiang425776024/article/details/87607301 ，最后会得出结论，问题的求解等价于关系，只要对其矩阵分解得到，就找到了w的解（最大维度<2）。

多分类的情况也是一样的，最后的关键也是对矩阵分解求w。

3.1LDA算法流程

有数据集：

，

希望降维到d

1） 计算类内散度矩阵Sw:：

2）计算类间散度矩阵Sb，u为所有样本均值向量：

　　　3) 计算矩阵

4）矩阵分解，得到最大的d个特征值及对应的d个特征向量,得到投影矩阵W

5) 对样本集中的每一个样本特征xi转化为新的样本

6) 得到输出新样本集：

---

numpy实现，加强对原理的理解： 

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, 2, -1]])
X = data[:, :-1]
Y = data[:, -1]

# 类别数
class_labels = np.unique(Y)
n_class = class_labels.shape[0]

# 类均值向量
mean_vec = []
for c in range(n_class):
    mean_vec.append(np.mean(X[Y == class_labels[c]], axis=0))

# 类内散度矩阵Sw
SW = np.zeros((3, 3))
for cl, mv in zip(class_labels, mean_vec):
    sc_matrix_class = np.zeros((3, 3))
    for row in X[Y == cl]:  # 所有X中类别=cl的样本
        row, mv = row.reshape(3, 1), mv.reshape(3, 1)
        sc_matrix_class += (row - mv).dot((row - mv).T)
    SW += sc_matrix_class

# Sb
all_mean_vec = np.mean(X, axis=0)
n_features = X.shape[1]
SB = np.zeros((n_features, n_features))
for i, mea_v in enumerate(mean_vec):
    n = X[Y == class_labels[i]].shape[0]
    mea_v = mea_v.reshape(n_features, 1)
    all_mean_vec = all_mean_vec.reshape(n_features, 1)
    SB += n * (mea_v - all_mean_vec).dot((mea_v - all_mean_vec).T)

# Sw^-1 Sb矩阵分解
e_val, e_vec = np.linalg.eig(np.linalg.inv(SW).dot(SB))

dindex = np.argsort(e_val)[-2:][::-1]
W = e_vec[dindex]
new_X = np.dot(W, X.T)
plt.scatter(new_X.T[:, 0], new_X.T[:, 1])
plt.show()

 

 

sklearn 实现3维到2维：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets.samples_generator import make_classification

X, y = make_classification(n_samples=1000, n_features=3, n_redundant=0, n_classes=3, n_informative=2,
                           n_clusters_per_class=1, class_sep=0.5, random_state=10)
# fig = plt.figure()
# ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
# ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker='o', c=y)

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X, y)
X_new = lda.transform(X)
plt.scatter(X_new[:, 0], X_new[:, 1], marker='o', c=y)
plt.show()

---

4 MDS 流形学习（Manifold Learning）

流形学习（Manifold Learning）的一类，多维缩放MDS要求原始空间中的样本之间的距离在低维空间中保持，思想是构造距离矩阵，然后矩阵分解，和前面的降维流程基本上是一致的，只是矩阵分解时的构造不一样，没有特别之处。

具体细节参考《机器学习》周志华 P228。或者博客：https://blog.csdn.net/AI_BigData_wh/article/details/78242052

MDS流程：

sklearn API:https://scikit-learn.org/stable/modules/generated/sklearn.manifold.MDS.html

from sklearn.datasets import load_digits
from sklearn.manifold import MDS
X, _ = load_digits(return_X_y=True)
X.shape

embedding = MDS(n_components=2)
X_transformed = embedding.fit_transform(X[:100])
X_transformed.shape

---

4.1 Isomap 等度量映射

  Isomap：通过“改造一种原本适用于欧氏空间的算法”，达到了“将流形映射到一个欧氏空间”的目的。

流形Manifold：“嵌入在高维空间中的低维流形”，最直观的例子通常都会是嵌入在三维空间中的二维或者一维流形。比如说一块布，可以把它看成一个二维平面，这是一个二维的欧氏空间，现在我们（在三维）中把它扭一扭，它就变成了一个流形（当然，不扭的时候，它也是一个流形，欧氏空间是流形的一种特殊情况）。

MDS 是针对欧氏空间设计的，对于距离的计算也是使用欧氏距离来完成的。如果数据分布在流形上欧氏距离不适用。

Isomap通过把数据点连接起来构成一个邻接 Graph 来离散地近似原来的流形，而测地距离也相应地通过 Graph 上的最短路径来近似，通过这样的距离计算，把 MDS 中原始空间中距离的计算从欧氏距离换为了流形上的测地距离。

如下图：两点间的距离不再是欧氏距离！！

 

算法流程： 核心就是把MDS的距离计算改为了最短路径（Dijikstra、Floyd）等算法的计算。

sklearn API:https://scikit-learn.org/stable/modules/generated/sklearn.manifold.Isomap.html#sklearn.manifold.Isomap

from sklearn.datasets import load_digits
from sklearn.manifold import Isomap
X, _ = load_digits(return_X_y=True)
X.shape

embedding = Isomap(n_components=2)
X_transformed = embedding.fit_transform(X[:100])
X_transformed.shape

Isomap等距映射算法有一个问题就是他要找所有样本全局的最优解，当数据量很大，样本维度很高时，计算非常的耗时，鉴于这个问题，出现了只关注局部的LLE

 

---

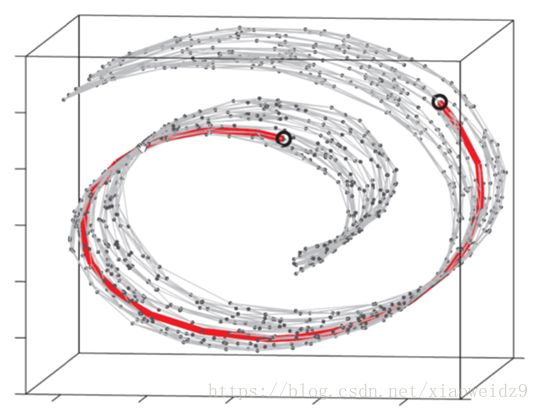
5 LLE 局部线性嵌入

局部线性嵌入(Locally Linear Embedding，以下简称LLE)，也是流形学习算法，LLE关注于降维时保持样本局部的线性关系，由于LLE在降维时保持了样本的局部关系，它广泛的用于图像图像识别，高维数据可视化等领域。

参考：https://www.cnblogs.com/pinard/p/6266408.html

LLE首先假设数据在较小的局部是线性的，也就是说，某一个数据可以由它邻域中的几个样本来线性表示，如原来的线性关系：

降维后的线性关系：

也就是说降维前后（局部）线性权重不变。

---

sklearn API:https://scikit-learn.org/stable/modules/generated/sklearn.manifold.locally_linear_embedding.html#sklearn.manifold.locally_linear_embedding

官方例子：https://scikit-learn.org/stable/auto_examples/manifold/plot_swissroll.html#sphx-glr-auto-examples-manifold-plot-swissroll-py

---

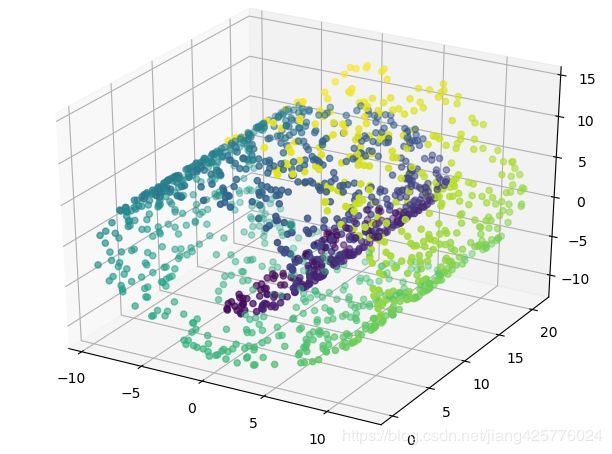
6 LE 拉普拉斯特征映射

其思路和LLE很相似，也是基于图的降维算法，希望相互关联的点降维后的空间尽可能靠近，通过构建邻接矩阵，最后推导，矩阵分解等步骤，实现降维。

sklearn API:https://scikit-learn.org/stable/modules/generated/sklearn.manifold.SpectralEmbedding.html#sklearn.manifold.SpectralEmbedding

from sklearn import manifold, datasets
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)

X, color = datasets.samples_generator.make_swiss_roll(n_samples=1500)

se = manifold.SpectralEmbedding(n_components=2, n_neighbors=10)
Y = se.fit_transform(X)
# 原3维
# ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color)
# 降维 2d
plt.scatter(Y[:, 0], Y[:, 1], c=color)
plt.show()

 

---