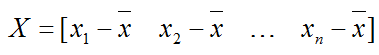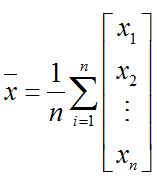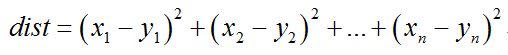PCA人脸识别学习及C语言实现
人脸识别主要方法:
.Eigenfaces,PCA(Principal Component Analysis),Turk and Pentland,1991
.Fisherfaces,LDA(Linear Discriminant Analysis),Belhumeur, Hespanha and Kriegman,1997
.LBPH,Local Binary Pattern Histograms,Ahonen, Hadid and Pietikäinen,2004
本文的目的,是结合人脸识别体验一把PCA,体会其内涵:降维。另外文献说,PCA的识别效果一般比神经网络ANN好。本文有20张人脸用于训练,10张人脸用于测试。
1.PCA人脸识别方法
将PCA方法用于人脸识别,其实是假设所有的人脸都处于一个低维线性空间,而且不同的人脸在这个空间中具有可分性。其具体做法是由高维 图像空间经PCA变换后得到一组新的正交基,对这些正交基做一定的取舍,保留其中的一部分生成低维的人脸空间,也即是人脸的特征子空间。PCA人脸识别算法步骤包括:
a.人脸图像预处理 【我没做,人脸大小都是高200,宽180】
b.读入人脸库,训练形成特征子空间 【特征值、特征向量的求法,采用我上一篇文章的QR算法】
c.把训练图像和测试图像投影到上一步骤中的特征子空间上 【矩阵相乘】
d.选择一定的距离函数进行判别 【欧氏距离,挑最小的匹配】
2.PCA人脸识别流程
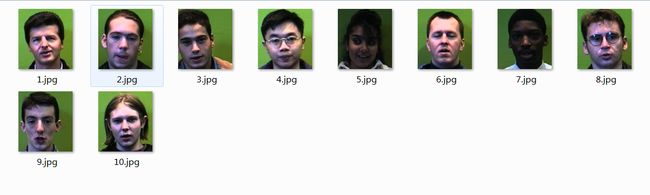
a.读入人脸库,读入每一个二维的人脸图像并转化为一维的向量,每个人选定一定数量的人脸照片构成训练集【共20张】,则训练集是一个36000*20的矩阵。测试集共10张图像,每次选一张,则测试集是一个36000*1的矩阵。
样本集:
测试集:
代码:
void load_data(double *T,IplImage *src,int k)
{
int i,j;
//一副图像压缩成一维的,存在T的一列里
for (i=0;iimageData[i*IMG_WIDTH+j];
}
}
}
b.计算 PCA变换的生成矩阵Q。首先计算训练集的协方差矩阵X,其中x1,x2,...,xn为第i副图像的描述,即xi为一个36000*1的列向量。
由于这个矩阵太大36000*36000,求特征值和特征向量比较坑,所以改为求 P=XTX 的特征向量和特征值,且有如下性质:
设e是矩阵P的特征值λ对应的特征向量,则有:
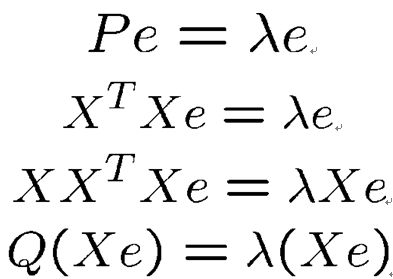
这里,X*e也是矩阵Q的特征值λ对应的特征向量,可以如此变换。
代码:
void calc_mean(double *T,double *m)
{
int i,j;
double temp;
for (i=0;ic.计算生成矩阵P的特征值和特征向量,并挑选合适的特征值和特征向量,构造特征子空间变化矩阵。这里P是实对称矩阵,可以采用上一篇的方法,先进行Household变换将P变成三对角矩阵,然后使用QR迭代算法求解特征值和特征向量,迭代次数60,误差eps=0.000001,代码:
void cstrq(double a[],int n,double q[],double b[],double c[])
{
int i,j,k,u,v;
double h,f,g,h2;
for (i=0; i<=n-1; i++)
for (j=0; j<=n-1; j++)
{ u=i*n+j; q[u]=a[u];}
for (i=n-1; i>=1; i--)
{ h=0.0;
if (i>1)
for (k=0; k<=i-1; k++)
{ u=i*n+k; h=h+q[u]*q[u];}
if (h+1.0==1.0)
{ c[i]=0.0;
if (i==1) c[i]=q[i*n+i-1];
b[i]=0.0;
}
else
{ c[i]=sqrt(h);
u=i*n+i-1;
if (q[u]>0.0) c[i]=-c[i];
h=h-q[u]*c[i];
q[u]=q[u]-c[i];
f=0.0;
for (j=0; j<=i-1; j++)
{ q[j*n+i]=q[i*n+j]/h;
g=0.0;
for (k=0; k<=j; k++)
g=g+q[j*n+k]*q[i*n+k];
if (j+1<=i-1)
for (k=j+1; k<=i-1; k++)
g=g+q[k*n+j]*q[i*n+k];
c[j]=g/h;
f=f+g*q[j*n+i];
}
h2=f/(h+h);
for (j=0; j<=i-1; j++)
{ f=q[i*n+j];
g=c[j]-h2*f;
c[j]=g;
for (k=0; k<=j; k++)
{ u=j*n+k;
q[u]=q[u]-f*c[k]-g*q[i*n+k];
}
}
b[i]=h;
}
}
for (i=0; i<=n-2; i++) c[i]=c[i+1];
c[n-1]=0.0;
b[0]=0.0;
for (i=0; i<=n-1; i++)
{ if ((b[i]!=0.0)&&(i-1>=0))
for (j=0; j<=i-1; j++)
{ g=0.0;
for (k=0; k<=i-1; k++)
g=g+q[i*n+k]*q[k*n+j];
for (k=0; k<=i-1; k++)
{ u=k*n+j;
q[u]=q[u]-g*q[k*n+i];
}
}
u=i*n+i;
b[i]=q[u]; q[u]=1.0;
if (i-1>=0)
for (j=0; j<=i-1; j++)
{ q[i*n+j]=0.0; q[j*n+i]=0.0;}
}
return;
}
//q:特征向量,b:特征值
int csstq(int n,double b[],double c[],double q[],double eps,int l)
{
int i,j,k,m,it,u,v;
double d,f,h,g,p,r,e,s;
c[n-1]=0.0; d=0.0; f=0.0;
for (j=0; j<=n-1; j++)
{ it=0;
h=eps*(fabs(b[j])+fabs(c[j]));
if (h>d) d=h;
m=j;
while ((m<=n-1)&&(fabs(c[m])>d)) m=m+1;
if (m!=j)
{ do
{ if (it==l)
{ printf("fail\n");
return(-1);
}
it=it+1;
g=b[j];
p=(b[j+1]-g)/(2.0*c[j]);
r=sqrt(p*p+1.0);
if (p>=0.0) b[j]=c[j]/(p+r);
else b[j]=c[j]/(p-r);
h=g-b[j];
for (i=j+1; i<=n-1; i++)
b[i]=b[i]-h;
f=f+h; p=b[m]; e=1.0; s=0.0;
for (i=m-1; i>=j; i--)
{ g=e*c[i]; h=e*p;
if (fabs(p)>=fabs(c[i]))
{ e=c[i]/p; r=sqrt(e*e+1.0);
c[i+1]=s*p*r; s=e/r; e=1.0/r;
}
else
{ e=p/c[i]; r=sqrt(e*e+1.0);
c[i+1]=s*c[i]*r;
s=1.0/r; e=e/r;
}
p=e*b[i]-s*g;
b[i+1]=h+s*(e*g+s*b[i]);
for (k=0; k<=n-1; k++)
{ u=k*n+i+1; v=u-1;
h=q[u]; q[u]=s*q[v]+e*h;
q[v]=e*q[v]-s*h;
}
}
c[j]=s*p; b[j]=e*p;
}
while (fabs(c[j])>d);
}
b[j]=b[j]+f;
}
for (i=0; i<=n-1; i++)
{ k=i; p=b[i];
if (i+1<=n-1)
{ j=i+1;
while ((j<=n-1)&&(b[j]<=p))
{ k=j; p=b[j]; j=j+1;}
}
if (k!=i)
{ b[k]=b[i]; b[i]=p;
for (j=0; j<=n-1; j++)
{ u=j*n+i; v=j*n+k;
p=q[u]; q[u]=q[v]; q[v]=p;
}
}
}
return(1);
}
void matrix_reverse(double *src,double *dest,int row,int col) //转置
{
int i,j;
for(i = 0;i < col;i++)
{
for(j = 0;j < row;j++)
{
dest[i * row + j] = src[j * col + i];
}
}
}
void matrix_mutil(double *c,double *a,double *b,int x,int y,int z) //矩阵乘法
{
int i,j,k;
for (i=0;i挑选合适的特征值和特征向量,其实就是挑特征值大于1的【关于挑选,可以排序选前k个,也可以设阈值】:
void pick_eignevalue(double *b,double *q,double *p_q,int num_q)
{
int i,j,k;
k=0;//p_q的列
for (i=0;i1)
{
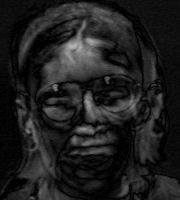
for (j=0;j d.把训练图像和测试图像投影到特征空间中。每一幅人脸图像投影到子空间以后,就对应与子空间的一个点。同样,子空间中的任一点也对应于一副图像。这些子空间的点在重构以后的图像很像人脸,所以他们被成为特征脸Eigenface。有了这样一个由特征脸组成的降维子空间,任何一副人脸图像都可以向其做投影并获得一组坐标系数,这组系数表明了该图像在子空间中的位置,这样原来的人脸图像识别问题就转化为依据子空间的训练样本点进行分类的问题。
【非必要步骤,特征脸如何重构,即 X*e,X大小为36000*20,e大小为20*k,每次只需将36000行的一列数据按照图像大小按行存储即可,这样就有k张特征脸图像】:
double *temp;
IplImage *projected;
char res[20]={0}; //file name
temp = (double *)malloc(sizeof(double)*IMG_HEIGHT*IMG_WIDTH*num_q);//按列存取
projected = cvCreateImage(cvSize(IMG_WIDTH,IMG_HEIGHT),IPL_DEPTH_8U,1);
//求特征脸
matrix_mutil(temp,T,p_q,IMG_WIDTH*IMG_HEIGHT,TRAIN_NUM,num_q);
for (i=0;iimageData[j*IMG_WIDTH+k] = (unsigned char)abs(temp[(j*IMG_WIDTH+k)*num_q+i]);
}
}
cvSaveImage(res,projected);
}
结果:
回到原题,我们已经对P使用QR算法求的特征向量和特征值,通过X*e得到了Q的特征向量eigenvector大小36000*k,它构成了降维子空间。接下来,分别让样本集和测试集的图像投影到该子空间中,即:eigenvector ' * X 等等,然后得到一组坐标系数。
计算Q的特征向量和样本集像子空间投影的代码:
void get_eigenface(double *p_q,double *T,int num_q,double *projected_train,double *eigenvector)
{
double *temp;
double tmp;
int i,j,k;
//IplImage *projected;
//char res[20]={0}; //file name
projected = cvCreateImage(cvSize(IMG_WIDTH,IMG_HEIGHT),IPL_DEPTH_8U,1);
//temp = (double *)malloc(sizeof(double)*IMG_HEIGHT*IMG_WIDTH*num_q);//按列存取
memset(eigenvector,0,sizeof(double)*IMG_HEIGHT*IMG_WIDTH*num_q);
memset(projected_train,0,sizeof(double)*TRAIN_NUM*num_q);
//求特征脸
//matrix_mutil(temp,T,p_q,IMG_WIDTH*IMG_HEIGHT,TRAIN_NUM,num_q);
/*for (i=0;iimageData[j*IMG_WIDTH+k] = (unsigned char)abs(temp[(j*IMG_WIDTH+k)*num_q+i]);
}
}
cvSaveImage(res,projected);
}*/
//求Q的特征向量X*e,矩阵相乘
temp = (double *)malloc(sizeof(double)*IMG_HEIGHT*IMG_WIDTH*num_q);
matrix_mutil(temp,T,p_q,IMG_HEIGHT*IMG_WIDTH,TRAIN_NUM,num_q);
//投影到子空间
matrix_reverse(temp,eigenvector,IMG_WIDTH*IMG_HEIGHT,num_q);
matrix_mutil(projected_train,eigenvector,T,num_q,IMG_WIDTH*IMG_HEIGHT,TRAIN_NUM);
free(temp);
} //读取测试图像
test_img = cvLoadImage(".\\TestDatabase\\4.jpg",CV_LOAD_IMAGE_GRAYSCALE);
projected_test = (double *)malloc(sizeof(double)*num_q*1);//在特征空间投影后的测试样本
for (i=0;iimageData[i*IMG_WIDTH+j] - m[i*IMG_WIDTH+j];
}
}
//将待测数据投影到特征空间
memset(projected_test,0,sizeof(double)*num_q);
matrix_mutil(projected_test,eigenvector,T_test,num_q,IMG_WIDTH*IMG_HEIGHT,1); e.把投影到特征子空间中的测试图像和样本集进行比较,确定待识别样本所属类别。本文使用欧氏距离计算坐标之间的距离:
//计算projected_test与projected_train中每个向量的欧氏距离
Euc_dist = (double *)malloc(sizeof(double)*TRAIN_NUM);
for (i=0;i=Euc_dist[i])
{
min = Euc_dist[i];
label = i;
}
}
printf("%d.jpg is mathcing!",label+1); 实验结果:
即测试集中的4.jpg和样本集中的7.jpg对应匹配
下面给出主函数及各个头文件声明:
My_Matrix.h:
#include
#include
void cstrq(double a[],int n,double q[],double b[],double c[]);
int csstq(int n,double b[],double c[],double q[],double eps,int l);
void matrix_mutil(double *c,double *a,double *b,int x,int y,int z);
void matrix_reverse(double *src,double *dest,int row,int col); Process.h:
#include "cv.h"
#include "highgui.h"
#define TRAIN_NUM 20
#define IMG_HEIGHT 200
#define IMG_WIDTH 180
void load_data(double *T,IplImage *src,int k);
void calc_mean(double *T,double *m);
void calc_covariance_matrix(double *T,double *L,double *m);
void pick_eignevalue(double *b,double *q,double *p_q,int num_q);
void get_eigenface(double *p_q,double *T,int num_q,double *projected,double *eigenvector);main.cpp:
// face_recognition.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include "Process.h"
#include "My_Matrix.h"
int _tmain(int argc, _TCHAR* argv[])
{
double *T,*L,*m,*b,*q,*c,*p_q,*projected_train,*T_test,*projected_test,*eigenvector,*Euc_dist;
double eps,temp;
int i,j,flag,iteration,num_q;
char res[20];
IplImage *tmp_img,*test_img;
T = (double *)malloc(sizeof(double)*IMG_HEIGHT*IMG_WIDTH*TRAIN_NUM); //原始数据
T_test = (double *)malloc(sizeof(double)*IMG_HEIGHT*IMG_WIDTH*1); //测试数据
m = (double *)malloc(sizeof(double)*IMG_HEIGHT*IMG_WIDTH); //平均值
L = (double *)malloc(sizeof(double)*TRAIN_NUM*TRAIN_NUM); //L=T'*T,协方差矩阵
b = (double *)malloc(sizeof(double)*TRAIN_NUM); //L的特征值
q = (double *)malloc(sizeof(double)*TRAIN_NUM*TRAIN_NUM); //L特征值对应的特征向量
c = (double *)malloc(sizeof(double)*TRAIN_NUM); //实对称三对角矩阵的次对角线元素
eps = 0.000001;
memset(L,0,sizeof(double)*TRAIN_NUM*TRAIN_NUM);
//存储图像数据到T矩阵
for (i=1;i<=TRAIN_NUM;i++)
{
sprintf(res,".\\TrainDatabase\\%d.jpg",i);
tmp_img = cvLoadImage(res,CV_LOAD_IMAGE_GRAYSCALE);
load_data(T,tmp_img,i);
}
//求T矩阵行的平均值
calc_mean(T,m);
//构造协方差矩阵
calc_covariance_matrix(T,L,m);
//求L的特征值,特征向量
iteration = 60;
cstrq(L,TRAIN_NUM,q,b,c);
flag = csstq(TRAIN_NUM,b,c,q,eps,iteration); //数组q中第j列为数组b中第j个特征值对应的特征向量
if (flag<0)
{
printf("fucking failed!\n");
}else
{
printf("success to get eigen value and vector\n");
}
//对L挑选合适的特征值,过滤特征向量
num_q=0;
for (i=0;i1)
{
num_q++;
}
}
p_q = (double *)malloc(sizeof(double)*TRAIN_NUM*TRAIN_NUM); //挑选后的L的特征向量,仅过滤,未排序
projected_train = (double *)malloc(sizeof(double)*TRAIN_NUM*num_q); //投影后的训练样本特征空间
eigenvector = (double *)malloc(sizeof(double)*IMG_HEIGHT*IMG_WIDTH*num_q);//Pe=λe,Q(Xe)=λ(Xe),投影变换向量
pick_eignevalue(b,q,p_q,num_q);
get_eigenface(p_q,T,num_q,projected_train,eigenvector);
//读取测试图像
test_img = cvLoadImage(".\\TestDatabase\\4.jpg",CV_LOAD_IMAGE_GRAYSCALE);
projected_test = (double *)malloc(sizeof(double)*num_q*1);//在特征空间投影后的测试样本
for (i=0;iimageData[i*IMG_WIDTH+j] - m[i*IMG_WIDTH+j];
}
}
//将待测数据投影到特征空间
memset(projected_test,0,sizeof(double)*num_q);
matrix_mutil(projected_test,eigenvector,T_test,num_q,IMG_WIDTH*IMG_HEIGHT,1);
//计算projected_test与projected_train中每个向量的欧氏距离
Euc_dist = (double *)malloc(sizeof(double)*TRAIN_NUM);
for (i=0;i=Euc_dist[i])
{
min = Euc_dist[i];
label = i;
}
}
printf("%d.jpg is mathcing!",label+1);
return 0;
}
1.将20副高200,宽180的图像,存入矩阵T中,36000*20
2.计算T的协方差矩阵L,20*20
3.求P的特征值b,20*1,特征向量q,20*20【q中的第j列向量即为b中第j个特征值对应的特征向量】,经过挑选后的特征向量num_q,20*k
4.构造特征子空间,即计算 T*p_q,得到eigenvector,36000*k,也是k副特征脸
5.将样本集图像投影到特征子空间,即计算eigenvector ' * T,得到一组坐标系数,projected_train,k*20,每一列为对应图像在子空间中的坐标
6.同理操作,得到测试图像在子空间中的坐标,projected_test,k*1
7.分别计算projected_tes和projected_train的坐标距离,选最小的匹配。
完整代码,下载地址:http://download.csdn.net/detail/jinshengtao/6870069