字符串算法:Trie树(前缀树)、后缀树
Trie树(前缀树)
Trie树,又称字典树、前缀树,是一种树形结构,是哈希树的变种,是一种用于快速检索的多叉树结构。
典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:最大限度地减少无谓的字符串比较,查询效率比哈希表高。
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。
Trie树也有它的缺点,Trie树的内存消耗非常大。
概念
假设有and,as,at,cn,com这些关键词,那么如何构建Trie树呢?
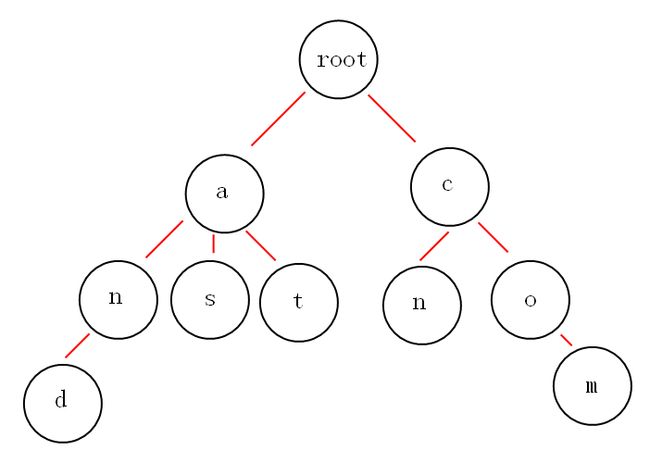
从上面可以发现一些Trie树的特性:
- 根节点不包含字符,除根节点外的每一个子节点都包含一个字符。
- 从根节点到某一节点的路径上的字符连接起来,就是该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
应用
字符串的快速检索
字典树的查询时间复杂度是O(logL),L是字符串的长度。所以效率还是比较高的。
hash表:
通过hash函数把所有的单词分别hash成key值,查询的时候直接通过hash函数即可,都知道hash表的效率是非常高的,为O(1)。对于单词查询,如果我们hash函数选取的好,计算量少,且冲突少,那单词查询速度肯定是非常快的。那如果hash函数的计算量相对大呢,且冲突率高呢?这些都是要考虑的因素。
另外hash表不支持动态查询,什么叫动态查询,当我们要查询单词apple时,hash表必须等待用户把单词apple输入完毕才能hash查询。当你输入到appl时肯定不可能hash吧。
字典树(tries树):
对于单词查询这种,还是用字典树比较好,但也是有前提的,空间大小允许,字典树的空间相比较hash还是比较浪费的,毕竟hash可以用bit数组。
字典树支持动态查询,比如apple,当用户输入到appl时,字典树此刻的查询位置可以就到达l这个位置,那么我在输入e时光查询e就可以了(更何况如果我们直接用字母的ASCII作下标肯定会更快)!字典树并不用等待你完全输入完毕后才查询。
字符串排序
先遍历字母序在前面的比如abdh,然后abdi。减少了没必要的strcmp,这个很好理解。
最长公共前缀
abdh和abdi的最长公共前缀是abd,遍历字典树到字母d时,此时这些单词的公共前缀是abd。
自动匹配前缀显示后缀
我们使用辞典或者是搜索引擎的时候,输入appl,后面会自动显示一堆前缀是appl的东东吧。
那么有可能是通过字典树实现的,前面也说了字典树可以找到公共前缀,我们只需要把剩余的后缀遍历显示出来即可。
指针模板的实现
Trie树可以用指针实现,也可以用数组来实现。首先介绍指针模板的实现。
定义trie树节点
其中的val存储以当前节点决定的前缀的个数,当然这个变量很灵活,也可以存储以当前节点决定的完整字符串的个数,所以需要具体问题具体分析。
#define MAX_CHILD 26 //如果是01字典树,就是2
struct Node {
int val;
Node* next[MAX_CHILD];
Node() {
count = 0;
memset(next, 0, sizeof(next));
}
};
新建一个空的Trie树很简单,只要:
Node* root = new Node();插入一个单词
void insert(Node* root, string str)
{
int len=str.size();
if(len == 0)
return;
for(int i=0;i<len;i++)
{
//如果不存在的话,我们就建立一个新的节点
if(root->next[s[i]-'a']==NULL)
root->next[s[i]-'a']=new Node();
root = root->next[s[i]-'a'];
//这里val表示前缀的个数,所以放在这里处理
root->val++;
}
}删除一个单词
void delete(Node* root, string str) {
int len=str.size();
if(len==0)
return;
for(int i=0;i<len;i++)
{
//如果分支还不存在,说明本来就不存在该单词,直接返回
if(root->next[s[i]-'a']==NULL)
return;
//如果分支存在,就将该分支的val减一
root = root->next[s[i]-'a'];
root->val--;
//如果前缀数量已经为0了,就可以把该分支删除了
if(root->val == 0)
delete root;
root = NULL;
}
}
}求以str为前缀的单词个数
int search(Node* root, string str) {
int len=str.size();
if(len==0)
return 0;
for(int i=0;i<len;i++)
{
//如果没有走到头就结束了,说明str根本不存在,直接返回0
if(root->next[s[i]-'a'] == NULL)
return 0;
//还有下个节点,继续查询
root = root->next[s[i]-'a'];
}
//返回以str为前缀的单词个数
return root->val;
}先往Trie树中插入n个单词,然后查找m次,每次返回以str为前缀的单词个数。完整代码为:
int main()
{
int m,n,i;
string str;
while(cin>>n) {
//先建立一个Trie树
Node* root = new Node();
for(i=0;icin>>str;
insert(root,str);
}
cin>>m;
//求以str为前缀的单词数量
for(i=0;icin>>str;
cout<return 0;
} 进一步举例:查找某完整字符串的个数
首先查找以该字符串str为前缀的单词数cnt1,然后查找以str+c为前缀的单词数cnt2,其中c为a、b、c、d…、z。而cnt1-cnt2就是以某str为完整匹配的字符串的个数了。因为如果不存在str这样的完整字符串,那么cnt1一定等于cnt2。
int search_complete(Node* root, string str)
{
int cnt1=0;
int cnt2=0;
cnt1=search(root,str);
for(int i=0;ichar c = 'a'+i;
string temp = str+c;
cnt2 += search_str(root,temp);
}
return cnt1-cnt2;
} 数组模板的实现
上面实现的是Trie树的指针模板,其实Trie可以用数组实现,这里姑且列出。在这种实现中,结点对儿子的指向是这样实现的:对每个结点开一个字母集大小的数组,对应的下标是儿子所表示的字母,内容则是这个儿子对应在大数组上的位置,即标号。
这种方法的空间要求较大,而且个人感觉没有指针的实现好理解。
注意,根据实现功能的不同,这里的Trie树就和上面的不一样。这里的val[i]存放的不再是节点i所决定的前缀的个数,而是以节点i为结尾的单词的值,当然这个值可以是单词的词频。
#includeint c=idx(s[i]);
if(!ch[u][c])//创建新的节点
{
CLR(ch[sz]);
val[sz]=0;//过程中的节点为0
ch[u][c]=sz++;//新建节点的编号
}
u=ch[u][c];//往下走
}
val[u]=v;//给插入的字符串的最后一个字符附加信息为v
}
bool Find(const char* s){
int u=0,n=strlen(s);
for(int i=0;i1;i++){
int c=idx(s[i]);
if(!ch[u][c]) return false;//没有当前节点。表示不存在
u=ch[u][c];
}
int c=idx(s[n-1]);
if(val[ch[u][c]]) return true;//判断最后一个节点是过程节点,还是终节点
return false;
}
};
Trie T;
int main()
{
T.Clear();
int n,m;
scanf("%d%d",&n,&m);
char tmp[maxn];
for(int i=1;i<=n;i++)
{
scanf("%s",tmp);
T.Insert(tmp,i);
}
for(int i=1;i<=m;i++)
{
scanf("%s",tmp);
if(T.Find(tmp)) printf("Found!\n");
else printf("Not Found!\n");
}
return 0;
} 求一个数组中任意2个数的最大异或值
这个问题可以用01-字典树很好地解决,即把所有数先按二进制从高到低位看成字符串插入trie。
枚举每个数,作为X,然后去trie里尽可能找每一位与X的二进制位相反的数,不断更新答案。
指针版:
class Solution {
public:
int findMaximumXOR(vector<int>& nums) {
//首先建立root
Node* root = new Node();
//将每个数先插入到Trie树中,构建Trie树
for(auto x : nums)
insert(root,x);
int ans = 0;
//再遍历一次数组,找到每个元素对应的最大异或值,然后再从中找最大的
for(auto x : nums)
{
int temp = x^query(root,x);
ans = max(ans,temp);
}
return ans;
}
struct Node {
int val;
Node* ch[2];
Node() {
val = 0;
memset(ch,NULL,sizeof(ch));
}
};
void insert(Node* root,int x)
{
int a;
for(int i=31;i>=0;i--)
{
a = (x>>i)&1;
//如果分支还不存在,就先建立分支
if(root->ch[a]==NULL)
root->ch[a] = new Node();
root = root->ch[a];
}
//在x的第0位,将x的值赋给val
root->val = x;
}
int query(Node* root,int x)
{
int a;
for(int i=31;i>=0;i--)
{
//a是x的第i位的取反
a = ((x>>i)&1)^1;
//向下尽可能找相异的分支
//如果相异的分支不存在
if(root->ch[a]==NULL)
a = (x>>i)&1;
root = root->ch[a];
}
return root->val;
}
};数组版:
class Solution {
private:
int ch[100000][2];//指向孩子节点的所在位置
int val[100000];//将一个整型x存进Trie后,其最后一位上的val保存了x的值
int sz;//树中节点个数
public:
int findMaximumXOR(vector<int>& nums) {
//初始化根节点
sz=1;
ch[0][0]=ch[0][1]=0;
val[0]=0;
//将每个数先插入到Trie树中,构建Trie树
for(auto i : nums)
insert(i);
int ans = 0;
//再遍历一次数组,找到每个元素对应的最大异或值,然后再从中找最大的
for(auto i : nums)
{
int temp = i^query(i);
ans = max(ans,temp);
}
return ans;
}
//将数x插入到Trie树中
void insert(int x)
{
int p=0;
for(int i=31; i>=0; i--)
{
int a=(x>>i)&1;
//如果分支还不存在,就建立分支
if(ch[p][a]==0)
{
//新建一个节点,编号为sz
ch[sz][1]=ch[sz][0]=0;
ch[p][a]=sz++;
}
p=ch[p][a];
}
//在x的第0位,将x的值赋给val
val[p]=x;
}
int query(int x)
{
int p=0;
for(int i=31; i>=0; i--)
{
int a=((x>>i)&1)^1;
//向下尽可能找相异的分支
//如果相异的分支不存在
if(ch[p][a]==0)
{
a=a^1;
}
p=ch[p][a];
}
return val[p];
}
};
后缀树
特点
后缀树,就是把一串字符的所有后缀保存并且压缩的字典树。相对于字典树来说,后缀树并不是针对大量字符串的,而是针对一个或几个字符串来解决问题,比如字符串的回文子串,两个字符串的最长公共子串等等。
性质:一个字符串构造了一棵树,树中保存了该字符串所有的后缀。
实现
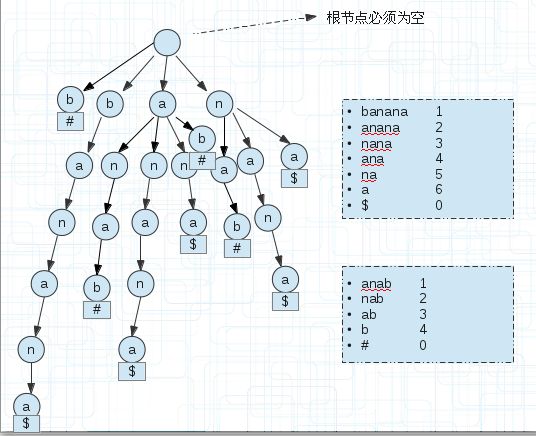
比如单词banana,它的所有后缀显示到下面的。1代表从第一个字符为起点,终点不用说都是字符串的末尾。

以上面的后缀,我们建立一颗后缀树。如下图,为了方便看到后缀,我没有合并相同的前缀。
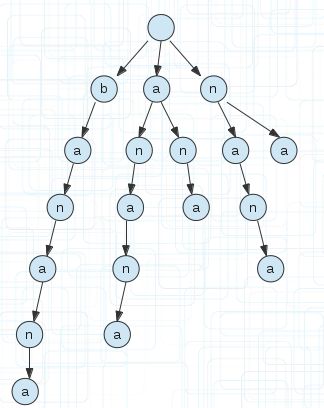
后缀树是把一个字符串所有后缀压缩并保存的字典树,所以我们把字符串的所有后缀还是按照字典树的规则建立,就成了上图的样子。
注意还是和字典树一样,根节点必须为空。
下面说下更加节省空间的方案,也就是上面提到的压缩。
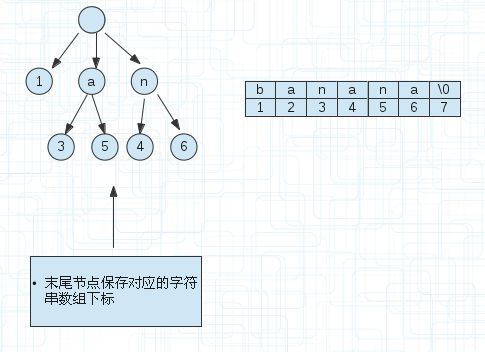
因为有些后缀串可能是单串,并不和其他的共用同一个前缀。
比如上图中的banana这个后缀串,直接可以用1来表示起点,终点是默认的。
上图的a节点后面有两个节点标记3和5是右边字符数组的下标,对应着a->3-7,a->5-7。因为a是共有的前缀。
应用
判断字符串s1是否是字符串s2的子串
这个很简单,如果s1在字符串s2中,那么s1必定是s2中某个后缀串的前缀。
比如banana,anan是anana这个后缀串的前缀。
获得字符串s1在字符串s2中重复的次数
比如说banana是s1,an是s2,那么计算an出现的次数实际上就是看an是几个后缀串的前缀。
a节点是保存所有起始为a字母的后缀串,我们看a字母后的n字母的引用计数即可。
两个字符串S1,S2的最长公共部分(广义后缀树)
先说下广义后缀树,前面说了后缀树可以存储一个或多个字符串,当存储的字符串数量大于等于2时就叫做广义后缀树。
建立一棵广义后缀树,如下图:
$和#是为了区分字符串的。
我们为每个后缀串末尾单独添加一个空间存储区分字符串的符号。那么怎么找s1和s2串最长的公共部分?遍历每个后缀串,如果其引用计数为1则直接跳过,因为不可能有两个子串存放在这里,当引用计数>1时,往下遍历,直到分叉分别记录子串的符号,如果不同,说明他们是不同字符串的,记录已经匹配的值即可,若相同继续下一次遍历。上图的ana部分,到ana时,子串$结束,然后继续向下,子串anab以#结束,那么匹配了ana。
最长回文串(广义后缀树)
把要求的最长回文串的字符串s1和它的反向(逆)字符串s2建立一棵广义后缀树。

回文串有一个定义就是正反相同,也就是正着和反着可以重和在一起,那么我们直接看这棵广义后缀树的共同前缀即可,每个banana的子串和ananab的子串重合的部分都是回文串,我们只需要找到最长的即可。比如上面的anana,从后面不同的标记可以看出两个字符串的某个后缀都有这个前缀,能完美重合到一起。即它是回文串。
记录Max,每次找到一个回文串比较即可。