【半监督分类】（一）半监督学习概述

半监督学习(Semi-Supervised Learning,SSL)类属于机器学习(Machine Learning,ML)。

一 ML有两种基本类型的学习任务：

1.监督学习(Supervised Learning,SL)

    根据输入-输出样本对L={(x₁,y₁),···,(x_l,y_l)}学习输入到输出的映射f:X->Y,来预测测试样例的输出值。SL包括分类(Classification)和回归(Regression)两类任务，分类中的样例x_i∈R^m(输入空间)，类标签y_i∈{c₁,c₂,···,c_c},c_j∈N;回归中的输入x_i∈R^m，输出y_i∈R(输出空间)。

2. 无监督学习(Unsupervised Learning,UL)

    利用无类标签的样例U={x₁,···,x_n}所包含的信息学习其对应的类标签Yu=[y₁···y_n]^T,由学习到的类标签信息把样例划分到不同的簇(Clustering)或找到高维输入数据的低维结构。UL包括聚类(Clistering)和降维(Dimensionality Reduction)两类任务。

二 半监督学习(Semi-Supervised Learning,UL)

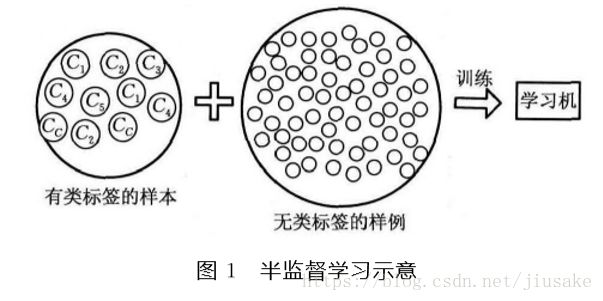
    在许多ML的实际应用中，很容易找到海量的无类标签的样例，但需要使用特殊设备或经过昂贵且用时非常长的实验过程进行人工标记才能得到有类标签的样本，由此产生了极少量的有类标签的样本和过剩的无类标签的样例。因此，人们尝试将大量的无类标签的样例加入到有限的有类标签的样本中一起训练来进行学习，期望能对学习性能起到改进的作用，由此产生了SSL，如如图１所示。SSL避免了数据和资源的浪费，同时解决了SL的 模型泛化能力不强和UL的模型不精确等问题。

1.半监督学习依赖的假设

SSL的成立依赖于模型假设，当模型假设正确时，无类标签的样例能够帮助改进学习性能。SSL依赖的假设有以下３个：

（１）平滑假设（Smoothness Assumption）

    位于稠密数据区域的两个距离很近的样例的类标签相似，也就是说，当两个样例被稠密数据区域中的边连接时，它们在很大的概率下有相同的类标签；相反地，当两个样例被稀疏数据区域分开时，它们的类标签趋于不同． 

（２）聚类假设（Cluster Assumption）

    当两个样例位于同一聚类簇时，它们在很大的概率下有相同的类标签．这个假设的等价定义为低密度分离假设（Low Sensity Separation Assumption），即分类 决策边界应该穿过稀疏数据区域，而避免将稠密数 据区域的样例分到决策边界两侧．

 （３）流形假设（Manifold Assumption）

    将高维数据嵌入到低维流形中，当两个样例位于低维流形中的一个小局部邻域内时，它们具有相似的类标签。许多实验研究表明当SSL不满足这些假设或模型假设不正确时，无类标签的样例不仅不能对学习性能起到改进作用，反而会恶化学习性能，导致 SSL的性能下降．但是还有一些实验表明，在一些特殊的情况下即使模型假设正确，无类标签的样例也有可能损害学习性能。

2.半监督学习的分类 

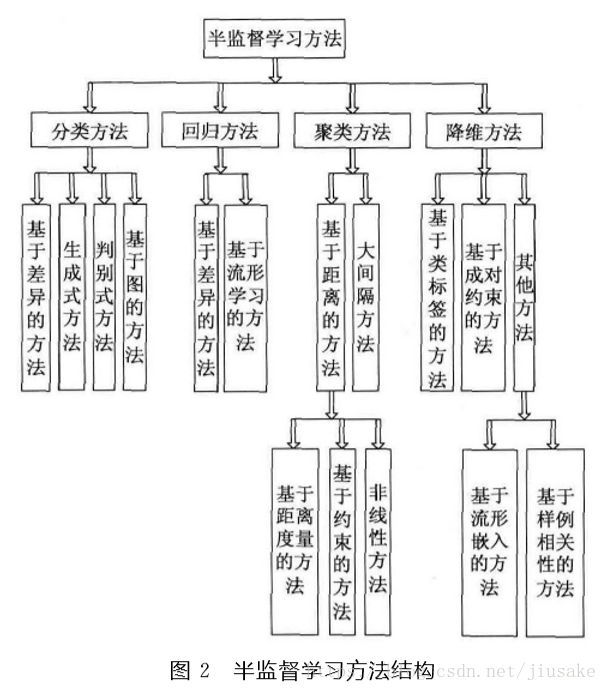
    SSL按照统计学习理论的角度包括直推 （Transductive ）SSL和归纳（Inductive）SSL两类模式。直推 SSL只处理样本空间内给定的训练数据，利用训练数据中有类标签的样本和无类标签的样例进行训练，预测训练数据中无类标签的样例的类标签；归纳SSL处理整个样本空间中所有给定和未知的样例，同时利用训练数据中有类标签的样本和无类标签的样例，以及未知的测试样例一起进行训练，不仅预测训练数据中无类标签的样例的类标签，更主要的是预测未知的测试样例的类标签。从不同的学习场景看，SSL可分为４大类： 

（１）半监督分类 （Semi-Supervised Classification）

    在无类标签的样例的帮助下训练有类标 签的样本，获得比只用有类标签的样本训练得到的分类器性能更优的分类器，弥补有类标签的样本不足的缺陷，其中类标签y_i取有限离散值y_i∈{c₁,c₂,···,c_c},c_j∈N。

（２）半监督回归（Semi-Supervised Regression）

    在无输出的输入的帮助下训练有输出的输入，获得比只用有输出的输入训练得到的回归器性能更好的回归器，其中输出y_i 取连续值 y_i∈Ｒ。 

（３）半监督聚类（Semi-Supervised Clustering）

    在有类标签的样本的信息帮助下获得比只用无类标 签的样例得到的结果更好的簇，提高聚类方法的精度。

（４）半监督降维（Semi-Supervised Dimensionality Reduction）

    在有类标签的样本的信息帮助下找到高维输入数据的低维结构，同时保持原始高维数据和成对约束（Pair-Wise Constraints）的结构不变，即在高维空间中满足正约束（Must-Link Constraints）的样例在低维空间中相距很近，在高维空间中满足负约束（Cannot-Link Constraints）的样例在低维空间中距离很远。