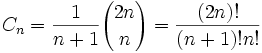卡特兰数——Catalan数
卡特兰数是组合数学中一个常出现在各种计数问题中出现的数列。由以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名。
通常使用的递归式: h(n)=((4*n-2)/(n+1))*h(n-1);
卡特兰数经常出现在ACM或者数论中,这是一个挺神奇的数列...
举个例子:给定节点数为N,问能组成多少种不同形状的二叉树?
【分析】
(1)先考虑只有一个节点的情形,设此时的形态有f(1)种,那么很明显f(1)=1
(2)如果有两个节点呢?我们很自然想到,应该在f(1)的基础上考虑递推关系。那么,如果固定一个节点后,左右子树的分布情况为1=1+0=0+1,故有f(2) = f(1) + f(1)
(3)如果有三个节点,(我们需要考虑固定两个节点的情况么?当然不,因为当节点数量大于等于2时,无论你如何固定,其形态必然有多种)我们考虑固定一个节点,即根节点。好的,按照这个思路,还剩2个节点,那么左右子树的分布情况为2=2+0=1+1=0+2。
所以有3个节点时,递归形式为f(3)=f(2) + f(1)*f(1) + f(2)。(注意这里的乘法,因为左右子树一起组成整棵树,根据排列组合里面的乘法原理即可得出)
(4)那么有n个节点呢?我们固定一个节点,那么左右子树的分布情况为n-1=n-1 + 0 = n-2 + 1 = … = 1 + n-2 = 0 + n-1。此时递归表达式为f(n) = f(n-1) + f(n-2)f(1) + f(n-3)f(2) + … + f(1)f(n-2) + f(n-1)
接下来我们定义没有节点的情况,此时也只有一种情况,即f(0)=1
那么则有:
f(0)=1,f(1)=1
f(2)=f(1)f(0)+f(0)f(1)
f(3)=f(2)f(0)+f(1)f(1)+f(0)f(2)
.
.
.
.
f(n)=f(n-1)f(0)+f(n-2)f(1)+……….+f(1)f(n-2)+f(0)f(n-1)
也就是先取一个点作为顶点,然后左边依次可以取0至N-1个相对应的,右边是N-1到0个,两两配对相乘,
就是h(n)=h(0)*h(n-1) + h(2)*h(n-2) + ...... + h(n-1)h(0)
N个节点的二叉树有h(n)种形状
能用卡特兰数解决的问题还有很多种
1、出栈次序问题。一个栈(无穷大)的进栈序列为1、2、3、...、n,有多少个不同的出栈序列?
举例:有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?
(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)
2、将多边行划分为三角形问题。将一个凸多边形区域分成三角形区域(划分线不交叉)的方法数?
举例:在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
//这道题曾经出现在一次ICPC中...印象挺深刻的...但是因为时间比较久所以具体是哪场已经忘记了...
因为在大数卡特兰数的计算时经常会用到取模运算,这里的取模运算需要记得有一点证明:
a/b % Mod = a % (b * Mod) /b % Mod;
遇到有除法的取模运算时,一定要注意这一点!
#include
#include
#include
#include
#include
#include
using namespace std;
const int N = 2000005;
const int n=148955;
bool a[N];
int pr[n];
#define MOD 1000000007
int num;
void Prime2()
{
memset(a, 0, N*sizeof(a[0]));
int i, j;
num = 0;
a[0]=a[1]=1;
for(i = 2; i < N; ++i)
{
if(!(a[i])) pr[num++] = i;
for(j = 0; (j>=1;
}
return ans;
}
int main()
{
/* FILE *p1,*p2;
p1=fopen("3.in","r");
p2=fopen("3.out","w");
*/ Prime2();
int txt,l=1,k,i;
long long ans,x,y;
while(~scanf("%d",&k) ){
memset(val,0,sizeof(val));
for(i=0;pr[i]<=2*k;++i)
calcJC(2*k,i,1);
for(i=0;pr[i]<=k;++i)
calcJC(k,i,-2);
ans=1;
for(i=0;pr[i]<=2*k;++i){
ans=(ans*MPow(pr[i],val[i]))%MOD;
}
extgcd(k+1,MOD,x,y);
x=(x+MOD)%MOD;
ans=(ans*x)%MOD;
printf("%lld\n",ans);
}
// fclose(p1);
// fclose(p2);
return 0;
} #include
#include
#include
using namespace std;
#define ALL(v) (v).begin(),(v).end()
#define cl(a,b) memset(a,b,sizeof(a))
#define clr clear()
#define pb push_back
#define mp make_pair
#define fi first
#define se second
typedef long long LL;
const LL mod = 1e9 + 7;
const int maxn = 1000000 + 10;
LL f[maxn];
//******************************
//返回d=gcd (a,b);和对应于等式ax+by=d中的x,y
long long extend_gcd (long long a,long long b,long long &x,long long &y)
{
if (a==0&&b==0) return -1;//无最大公约数
if (b==0){x=1;y=0;return a;}
long long d=extend_gcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
//*********求逆元素*******************
//ax = 1(mod n)
long long mod_reverse (long long a,long long n)
{
long long x,y;
long long d=extend_gcd(a,n,x,y);
if (d==1) return (x%n+n)%n;
else return -1;
}
void init()
{
f[0] = 1;
for( int i = 1; i < maxn; i++ ){
LL ret = mod_reverse(i+1,mod);
f[i] = f[i-1] * (4 * i - 2) % mod * ret % mod;
}
}
int main()
{
init();
int n;
while(~scanf("%d",&n)){
assert(1 <= n && n <= 1000000);
printf("%lld\n",f[n]);
}
return 0;
}