冠军算法变体合集再上新!具有新的变异策略和外部归档机制的改进LSHADE-SPACMA算法
1 简介
算法提出了一种用于数值优化和点云配准的LSHADE-SPACMA(mLSHADE-SPACMA)的修改版本。首先,提出了一种精确的消除和生成机制,以增强算法的局部开发能力。其次,引入了一种基于改进的半参数自适应策略和基于秩的选择压力的变异策略,改进了算法的进化方向。第三,提出了一种基于精英的外部归档机制,保证了外部种群的多样性,可以加速算法的收敛进度。
2.7 LSHADE-SPACMA
2.7.1 半参数自适应策略
参数配置在差分进化算法的性能中起着至关重要的作用,自适应参数设置表明算法性能与为给定问题选择的特定参数密切相关。不同的问题可能需要定制的参数值来优化算法性能(Das et al. 2016)。为了促进 F i F_i Fi和 C R i CR_i CRi的半参数自适应,LSHADE-SPA在LSHADE算法的前一半评估时间内修改了 F i F_i Fi的计算方法。具体公式如下:
F i = 0.45 + 0.1 ⋅ r a n d , F E s < max F E s / 2 ( 31 ) F_i = 0.45 + 0.1 \cdot rand, \ FEs < \max FEs/2 \quad (31) Fi=0.45+0.1⋅rand, FEs<maxFEs/2(31)
2.7.2 LSHADE-SPACMA混合框架
为了提高算法的效率,开发了一个结合LSHADE-SPA和改进的CMA-ES算法的混合框架。交叉操作被引入到CMA-ES算法中以增强框架的探索功能。交叉操作根据CMA-ES步骤生成后代后的公式(4)执行。
整个框架从一个公共种群 P P P开始,其中种群中的每个个体 x x x可以通过LSHADE或CMA-ES生成后代个体 u u u。这些个体的分配基于一个类概率变量 ( F C P ) (FCP) (FCP),其值从每个算法的槽 M F C P M_{FCP} MFCP中随机选择。在每一代结束时,根据每个算法的性能更新内存槽 M F C P M_{FCP} MFCP,从而逐渐增加分配给表现更好的算法的种群比例。仅在成功生成新个体的情况下执行更新过程。具体的 M F C P M_{FCP} MFCP内存槽更新机制如下:
M F C P , g + 1 = ( 1 − c ) ⋅ M F C P , g + c ⋅ Δ A l g 1 ( 32 ) M_{FCP,g+1} = (1 - c) \cdot M_{FCP,g} + c \cdot \Delta_{Alg1} \quad (32) MFCP,g+1=(1−c)⋅MFCP,g+c⋅ΔAlg1(32)
在更新机制中,变量向量 c c c用于调整每次更新的大小。不同变异算子的改进率 Δ A l g 1 \Delta_{Alg1} ΔAlg1表示算法从一代到下一代的性能改进,使用公式(33)计算。
Δ A l g 1 = min ( 0.8 , max ( 0.2 , ω A l g 1 / ( ω A l g 1 + ω A l g 2 ) ) ) ( 33 ) \Delta_{Alg1} = \min (0.8, \max (0.2, \omega_{Alg1} / (\omega_{Alg1} + \omega_{Alg2}))) \quad (33) ΔAlg1=min(0.8,max(0.2,ωAlg1/(ωAlg1+ωAlg2)))(33)
其中0.2和0.8分别表示分配给每个变异算子的最小和最大概率值。这是为了确保两种算法可以同时运行,保持算法多样性和平衡探索与开发的能力。因此, F C P FCP FCP的值始终保持在0.2和0.8之间。此外, ω A l g 1 \omega_{Alg1} ωAlg1表示算法 A l g 1 Alg1 Alg1的新旧适应度值之间的差异累积,并作为评估该算法下每个个体性能变化的指标,如公式(34)所示。
ω A l g 1 = ∑ i = 1 n f ( x i ) − f ( u i ) ( 34 ) \omega_{Alg1} = \sum_{i=1}^{n} f(x_i) - f(u_i) \quad (34) ωAlg1=i=1∑nf(xi)−f(ui)(34)
3 提出的mLSHADE-SPACMA方法
3.1 动机
改进LSHADE-SPACMA算法的动机主要来自于其在处理不同优化问题时的性能瓶颈,主要包括未能充分利用当前种群信息进行迭代过程,导致局部搜索能力不足。同时,半参数自适应策略的敏感性分析缺乏,削弱了算法在不同问题场景中的适应性。此外,变异策略有时无法有效引导进化方向,外部存档更新机制的随机性可能会移除优秀个体,影响种群多样性和算法的整体质量。因此,通过引入更准确的淘汰和生成机制,改进变异策略,并优化外部存档机制,提高了算法的整体性能和收敛速度,以更好地解决各种优化问题。
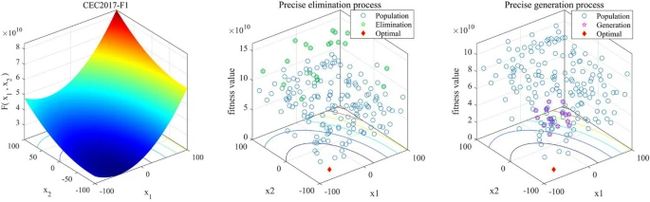
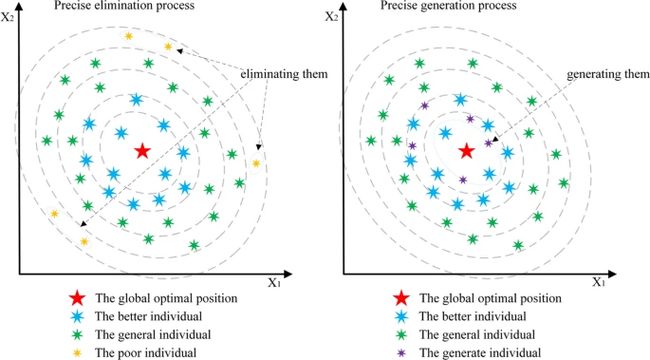
3.2 精确淘汰和生成机制
淘汰种群中最差的个体和精英引导已被广泛用于提高算法性能(Chauhan and Shivan 2024; Chauhan and Yadav 2024a),其中大多数是不精确的。在mLSHADE-SPACMA中,我们提出了一种精确的淘汰和生成机制,以确保解决方案的高质量。值得注意的是,该机制仅在评估的前一半期间运行。受自然选择中“适者生存”现象的启发,该机制通过以下具体步骤实现:
在一轮评估后,识别出适应度较差的个体进行淘汰。该过程的选择机制如下所示:
P E m = c e i l ( ρ ⋅ N P ) , F E s < max F E s / 2 ( 35 ) PE_m = ceil (\rho \cdot NP), \ FEs < \max FEs/2 \quad (35) PEm=ceil(ρ⋅NP), FEs<maxFEs/2(35)
其中 P E m PE_m PEm表示要淘汰的个体数量, c e i l ceil ceil表示大于或等于自身的最小整数, ρ \rho ρ表示要淘汰的种群百分比。根据适应度排名选择淘汰个体,确保最低性能的个体被移除。随后,通过以下生成机制生成等量的
markdown复制
在提高个体进化方向的同时,我们进行了参数敏感性分析,并修改了原始LSHADE-SPACMA缩放因子 F i F_i Fi的半参数自适应策略,如公式(37)所示。
F i = 0.5 + 0.1 ⋅ r a n d , F E s < M a x F s / 2 ( 37 ) F_i = 0.5 + 0.1 \cdot rand, \ FEs < MaxFs/2 \quad (37) Fi=0.5+0.1⋅rand, FEs<MaxFs/2(37)
为了增强LSHADE-SPACMA的局部开发能力,将LSHADE-RSP中的RSP策略集成进来。在mLSHADE-SPACMA中,使用公式(7)、公式(22)和公式(37)定义了新的变异策略,最终形成了公式(38)中详细描述的策略,并命名为mLSHADE。与LSHADE-RSP不同,缩放因子 F i F_i Fi采用了改进的半参数自适应策略来维持种群多样性。此外,本研究仅对 r 1 r_1 r1应用RSP策略,增强了 x p r 1 x_{pr_1} xpr1优于 x r 2 x_{r_2} xr2的可能性,从而增加了种群进化方向改善的概率。此外,外部存档机制得到了充分利用,特别是在进化的后期阶段,随机选择 x r 2 x_{r_2} xr2可以显著提高种群多样性。
v i = x i + F i ⋅ ( x p b e s t − x i ) + F i ⋅ ( x p r 1 − x r 2 ) ( 38 ) v_i = x_i + F_i \cdot (x_{pbest} - x_i) + F_i \cdot (x_{pr_1} - x_{r_2}) \quad (38) vi=xi+Fi⋅(xpbest−xi)+Fi⋅(xpr1−xr2)(38)
3.4 精英存档机制
在LSHADE-SPACMA中,当存档大小超过预定阈值时,会随机移除一部分个体,这可能会无意中消除高质量解决方案并降低存档的质量和多样性。为了解决这些缺点,提出的mLSHADE-SPACMA采用了一种精英存档机制,旨在通过确保只有最佳个体保留在外部存档中来优化算法性能。这种方法旨在在优化过程中保持存档的质量和多样性,并防止劣质解决方案的持续存在。
具体来说,当存档大小|A|超过预设限制时,替换LSHADE-SPACMA使用的随机移除方法。相反,根据其适应度值筛选个体,并选择性地消除适应度较差的个体。这种精英存档机制保证了存档中始终充满高度适应的个体,在整个优化过程中不断引导搜索朝着更优的解决方案空间发展。这种增强不仅提高了算法的收敛精度,还提高了解决方案的多样性和算法的鲁棒性。
Fu, S., Ma, C., Li, K. et al. Modified LSHADE-SPACMA with new mutation strategy and external archive mechanism for numerical optimization and point cloud registration. Artif Intell Rev 58, 72 (2025). https://doi.org/10.1007/s10462-024-11053-1