浅谈Splay Tree(伸展树)及其实现

        最近学习了平衡树中的Splay Tree，现在分享一下个人对它的理解和本人的c++代码实现。若阅读过程有任何疑问或讲得不明白的地方，欢迎评论区留言。

---

基本概念

二叉搜索树（BST）： 
        指一棵二叉树，对于所有的子树，都满足左儿子及其所有子孙节点的值小于根节点值，根节点的值小于右儿子及其所有子孙节点的值。通过这一特性，我们可以在二叉搜索树上用log(n)的复杂度快速寻找到目标。

平衡二叉树：
        一棵能够保持左右子树高度尽量接近的二叉搜索树。

一个节点x的前驱：小于x，且最大的节点
一个节点x的后继：大于x，且最小的节点

 

SplayTree的功能

        Splay Tree的中文是“伸展树”，顾名思义就是通过类似伸展的操作实现一棵平衡二叉树。通过splay tree，我们可以实现对某些元素的快速插入、删除、查找等功能。
自编实例：
        一个人往墙上射箭，在第秒会射出一支箭，箭最终会插在离地米的位置。有时箭插得不牢固，高度为的那支箭会在第秒掉到地上。这个人一共会射出支箭。现在请输出每支箭被射出后，在墙上没掉下来的箭中，有多少支箭高度在区间里。这个问题涉及到了动态插入数据（射箭的高度），动态删除数据（箭掉了下来），动态查询数据（找高度为的箭），动态查询排名（找高度为和的箭在所有箭中的高度排名，相减再加一即为区间里箭的数量），如果直接暴力操作（比如用vector存高度+排序+二分查找），那么显然耗时巨大。于是平衡树的作用就体现在这里了：以非常短的时间复杂度完成这些操作（Splay树均摊复杂度logn）。

普通BST的缺点
        对于一棵普通的BST，如果每次插入节点时仅仅按照BST的定义来插入，那么这棵树很容易产生长链（如下面的例子）。如果长链较多，那么插入、查找操作的复杂度就会从O(logn)退化到接近O(n)，这不是我们所期盼的。

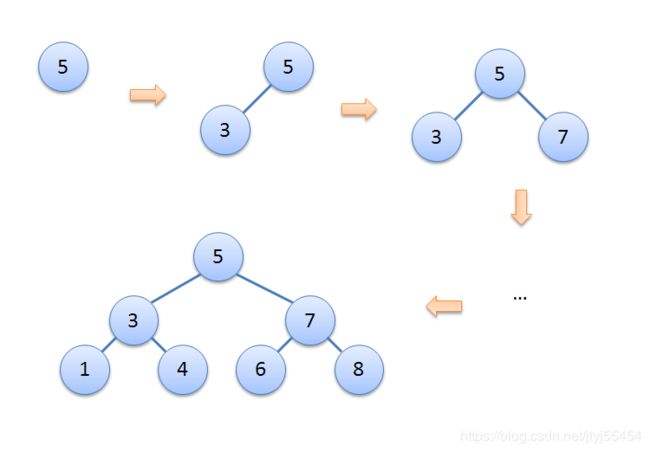
理想情况：
操作顺序： 插入5 -> 插入3-> 插入7-> 插入1-> 插入4> 插入6 -> 插入8 
此时操作任何元素都能在O(logn)的时间内完成

 

最坏情况：
操作顺序：插入5 -> 插入4 -> 插入3 -> 插入2 -> 插入1
此时操作元素的复杂度就非常接近O(n)了

可以看到，以某种特定顺序插入的数据会在没有平衡功能的BST中产生长链，Splay Tree则可以通过一系列操作规避以上坏情况。

 

SplayTree具体实现

        SplayTree保持平衡的基本思想：每次对树进行操作时都把节点们“旋转”一下，长链就会变短。

        在OI中，我们可以通过多个数组表示结点信息从而实现SplayTree。但个人认为，这样就等于把本应属于一类的信息分散开来，不能体现出“结点”和“树”的概念，还浪费了C++的面向对象特性。用指针和结构体来实现，在操作时我们就能很清晰地知道自己正在操作的是一个结点，这样更利于理解和减少错误。所以，本文的SplayTree通过指针和结构体实现。

1.结点结构体
        首先，我们定义一个树结点的结构体，包含几个基本变量和方法：

struct node{
    public:
    node *son[2];//son[0]和son[1]分别表示左右儿子节点指针
    node *father;//父亲节点指针
    int value;//节点的值
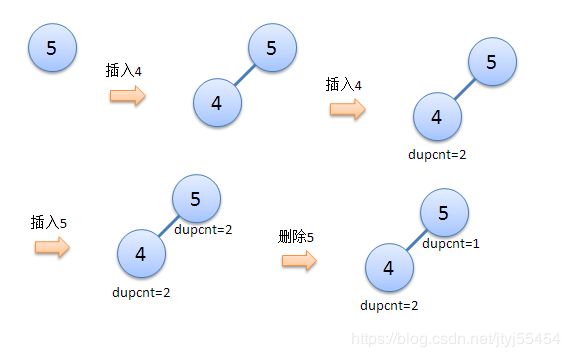
    int dupcnt;//这个结点值重复的个数（被重复插入过多少次）
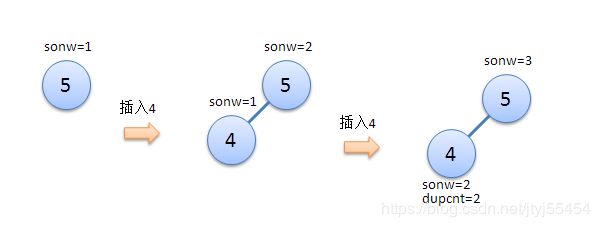
    int sonw;//子树大小（包括自己）

    node(){
        father=son[0]=son[1]=NULL;
        value=dupcnt=sonw=0;
    }

    //如果自己是父亲的左结点就返回0，否则1
    inline bool whichson(){
        if(father==NULL)return 0;//自己是根节点，返回0/1无影响
        return father->rts()==this;
    }

    //返回左儿子
    inline node* lfs(){
        return son[0];
    }

    //返回右儿子
    inline node* rts(){
        return son[1];
    }

    //更新函数，如果子树有变化就要调用
    //子树大小=左子树大小+右子树大小+自己的大小(dupcnt)，要特判没有左/右子树(指针为NULL)的情况
    inline void update(){
        sonw=(lfs()!=NULL?lfs()->sonw:0) + (rts()!=NULL?rts()->sonw:0)+dupcnt;
    }

    //回收内存时用的，OI中可以不写
    void clearSon(){
        if(son[0]!=NULL)son[0]->clearSon(),delete son[0];
        if(son[1]!=NULL)son[1]->clearSon(),delete son[1];
    }
};

        需要说明的是，value指的是该节点所存的数据，可以换成long long等任何实现了< > ==操作符的对象，包括各种自定义结构体。由于BST中不能含有两个值相同的节点，那么为了能够表示树中有重复的节点，我们需要用变量dupcnt来表示某个值重复的次数，即记录这个值被插入了多少次。当我们在树中插入一个已经存在的值时，那么就应该把dupcnt+1而不是再创建一个新节点。sonw表示以当前节点为根的子树的节点数，包括自己和重复的节点，update()函数在后面的splay()函数中会用到，这是一个更新节点信息的函数。

 

2.SplayTree的主体

struct SplayTree{
    node *root;
    SplayTree(){
        root=NULL;
    }
    //各种方法...
}

公共变量就只有这一个，根节点的指针

两个工具方法(utility)：
1.创建一个新节点：

node* createNode(int val){
    node *n=new node();
    n->value=val;
    n->dupcnt=1;//重复次数为1，即这个刚创建的节点在树里只出现过一次
    return n;
}

2.把一个节点连接到另一个节点的左/右儿子上

//把from节点连接到newfa节点的whichside(0=左,1=右)儿子上
void link(node *from,node *newfa,int whichside){
    if(newfa!=NULL)newfa->son[whichside]=from;
    if(from!=NULL)from->father=newfa;
}

之所以要判断！=NULL，是因为以后的操作过程中可能会遇到以下两种特殊情况：
①把一个节点变成根，根的父亲为null (newfa为null)
②要把一个结点A的左儿子连到另一个结点B上，但A并没有左儿子 (from为null)

SplayTree中最核心的两个操作：

①rotate：
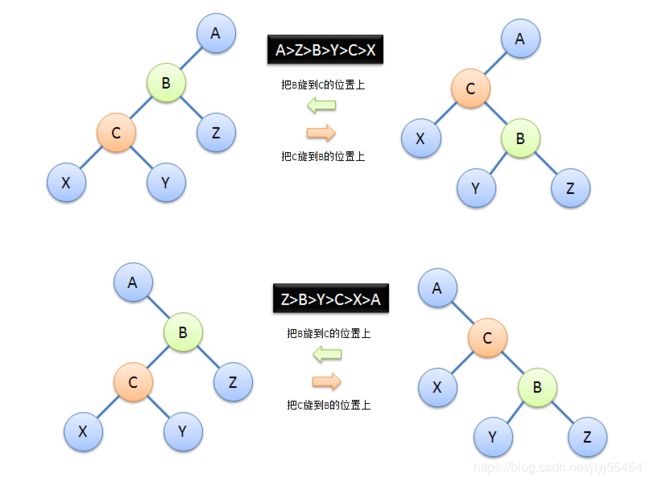
        旋转节点，是平衡树中几乎都会有的操作。它的功能是，在不改变树的BST性质的前提下，把一个结点“提”到父亲的位置上（使其深度减一）。如下图所示，不难想到一共会有四种情况：

可以看到旋转前后节点的大小关系都是不变的。

这其实就是所谓左旋(Zag)和右旋(Zig)，但观察它们的共同点，发现旋转过程可以归纳为以下三步：
对于要被拉高的结点：
①把和自己方向相反的儿子连到自己的父亲上，且方向和自己相同
②把父亲连到自己上，方向和自己的方向相反
③把自己连到爷爷上，方向和父亲相同

即：
反向子代我位，父代反向子位，我代父位
（注重理解，但强行记下来实际上也不难）

于是我们得到了左右旋的合并版rotate：

void rotate(node *n){
    if(n==root)return;
    node *fa=n->father;//父亲
    node *grf=fa->father;//爷爷
    int whichside=n->whichson();//我的位置
    int fawh=fa->whichson();//父亲的位置
    link(n->son[whichside^1],fa,whichside);//反向子连父亲(反向子代我位)
    link(fa,n,whichside^1);//父亲连到自己上(父亲代反向子位)
    link(n,grf,fawh);//我连到爷爷上(我代父位)
    fa->update();n->update();//记得更新，且顺序不能反
}

 

②splay：
        上面实现的rotate()每次只能把一个结点旋转上去一级，所以我们需要splay函数，把某个节点通过一系列旋转转移到目标节点的下方，同时保持二叉搜索树的性质（当然，目标节点必须是被旋转节点的祖先）。

//把sp旋转为target的儿子，target默认为null，表示旋转到根节点
//因为根节点没有父亲(father为null)，所以target设为null可以把节点旋转到根
void splay(node *sp,node *target=NULL){
    while(sp->father!=target){
        node *fa=sp->father;//父亲
        node *grf=fa->father;//爷爷
        //如果爷爷还不是目标，并且自己的方向和父亲的方向相同(都是各自父亲的左/右结点)
        //那么就先选择父亲再旋转自己，否则连续旋转自己两遍
        if(grf!=target){
            if(sp->whichson()==fa->whichson())rotate(fa);
            else rotate(sp);
        }
        rotate(sp);
    }
    if(target==NULL)root=sp;//如果要旋转到根节点，记得更改root
}

重点：这里的splay函数用到了“双旋”，即第一个if前注释所讲到的，为什么不直接写成下面这样，每次往上旋转一层，直到到达目标就完事了呢？

void splay(node *sp,node *target=NULL){
    while(sp->father!=target)rotate(sp);//单旋
    if(target==NULL)root=sp;
}

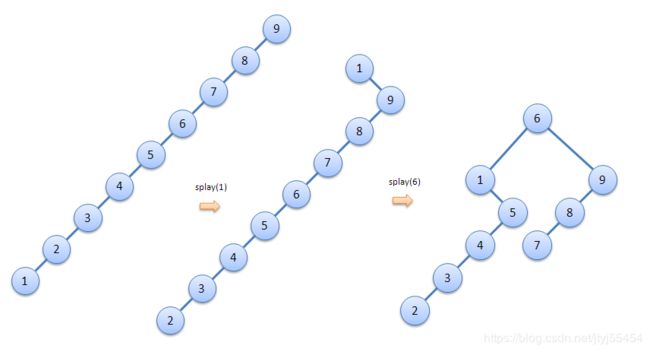
绝大多数博客都在splay()函数里用了双旋，而这样做的原因却只是用“防止被卡”等一笔带过。经过我的实验，双旋可以让树更加平衡。举个例子，现有下面这棵退化成了链的树，我们对它进行以下操作：查询1的排名->查询6的排名（查询排名操作需要用到splay()，下文会讲到），完成这两步操作后树的形态如下图所示：

使用双旋时：

使用单旋时：

可以看到，对于链这种极端情况，使用双旋可以使树的形态发生很大变化，操作一次就已经让树平衡许多；单旋版的splay操作一次后树仍然是一条链，操作两次后是两条不短的链。具体每一小步可以人手模拟一下，体会双旋到底对树的平衡作出了怎样的贡献。总之，使用双旋不仅不影响splay()的速度，还能降低以后操作的时间复杂度，何乐而不为？
注：事实上，每进行一次双旋型splay，把某节点旋转到根后该节点原来所在链的长度就会减半。

 

接下来是SplayTree中的一些功能性函数。

查找节点
      首先实现一个小小的辅助函数chooseSon，表示val大于当前节点的值时返回右儿子，否则左儿子。

node* chooseSon(node *n,int val){
    if(n->value>val)return n->son[0];
    else return n->son[1]; 
} 

      查找值为val的节点并旋转到根。根据二叉搜索树的性质查找即可。需要注意的是，如果val不存在，那么找到的是val的前驱或后继(最接近x的那个值，比它大还是小取决于那时树的结构)。

void find(int val){
    if(root==NULL)return;
    node *cur=root;
    while(chooseSon(cur,val)!=NULL && cur->value!=val){
        cur=chooseSon(cur,val);
    }
    splay(cur);
}

 

找前驱/后继
      这个很好想，用find函数把val旋转到根，那么根的左儿子的最右子孙就是前驱；右儿子的最左子孙就是后继。

node* getPre(int val){//找val的前驱
    find(val);
    if(root->value < val)return root;
    node *cur=root->lfs();
    if(cur==NULL)return root;//val比树里最小的值还小，为了让返回值不为null，就直接返回root
    while(cur->rts() != NULL)cur=cur->rts();
    return cur;
}

       需要说明的是，if(root->value < val)return root;这句是一定要加进去的。回顾“找x前驱”的定义，是找树里比x小的最大的数，但这里的x没有特指一定要是树里已经存在的值，而如果树里没有x这个值，调用find(x)后根节点的值是不确定的(刚刚讲过)。如果find(x)后被旋转到根的节点的值比x小，那么说明此时树里没有x，并且现在的根节点就已经是前驱了。所以加上那句的就是为了特判这种情况。
      找后继同理。

 

插入/删除操作

插入：
        和find差不多，根据二叉搜索树的性质找到应插入的地方，然后插入即可

//插入val
void insertNode(int val) {
    if(root == NULL) {//当前是空树，特判
        root=createNode(val);
        root->update();
        return;
    }
    node *cur=root;
    //不停chooseSon，查找val的位置
    while(chooseSon(cur,val)!=NULL && cur->value!=val) {
        cur=chooseSon(cur,val);
    }
    //如果找到了一个值和val相等，说明以前已经添加过了，直接dupcnt++
    if(cur->value == val) {
        cur->dupcnt++;
        splay(cur);//splay一下，保持平衡
        return;
    }
    //如果找不到，那就只有一种情况：
    //cur的值最接近val，val应成为cur的儿子
    int bw=val > cur->value;
    node *c=createNode(val);
    //bw决定添加到左还是右儿子，不难证明这时c应插入到的位置肯定为空
    link(c,cur,bw);
    splay(c);
}

删除： 
        删除的细节较多。如果删除一个没有儿子的结点，那么直接设其父亲的儿子为null即可，但如果要删除的节点也有儿子怎么办？我们先看一个结论：如果前驱在根节点，后继是根节点的右儿子，那么后继的左儿子就是自己，并且自己是叶子节点。

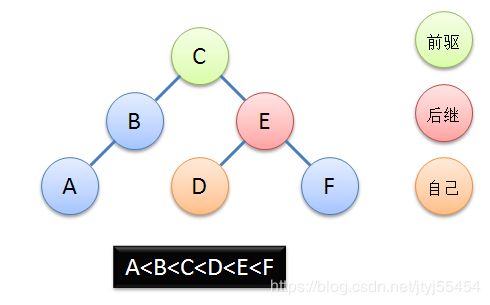
        借助这幅图，这个结论不难证明。所以，删除操作的核心就是：把前驱旋转到根，把后继旋转到根的下面，然后删除后继的左儿子。这样就避免了要删除的节点有儿子的情况。但注意要特判要删除的结点已经是整棵树里最小/最大的结点的情况，因为此时它没有前驱/后继。

//删除一个节点，进行内存回收等操作
void _delN(node *n) {
    if(n->dupcnt > 1) {//节点重复数大于1，直接dupcnt--，记得update
        n->dupcnt--;
        n->update();
    } else {
        if(n==root) {//删除根，特判
            delete root;
            root=NULL;
        } else {//一般情况，记得修改父亲，更新父亲
            n->father->son[n->whichson()]=NULL;
            n->father->update();
            delete n;
        }
    }
}

void deleteNode(int val) {
    node *pre=getPre(val);
    node *post=getPost(val);
    if(pre->value==val && post->value==val) {
        _delN(root);
        return;
    }
    if(pre->value== val) {
        splay(post);_delN(pre);
        return;
    }
    if(post->value == val) {
        splay(pre);_delN(post);
        return;
    }
    splay(pre);//前驱旋转到根
    splay(post,pre);//后继旋转到根下面
    _delN(post->lfs());//删除后继的左儿子
}

 

查找排名/查找第k大数
        利用SplayTree，我们还可以实现查询某个值在树中是第几大和树中第k大的数是几。
        查找一个数的排名，我们把它选择到根，左子树的大小+1就是答案。当然，这个排名也可以表示为子树大小 - 右子树大小 - 重复次数+1(这里就用了这种更麻烦的方法)
        查找第k大的数，我们可以根据k的大小，从根节点开始往下走，直到找到目标。

//返回以某个节点的左/右儿子为子树的节点数。
int getChildCnt(node *n,int whichside) {
    if(n->son[whichside]==NULL)return 0;
    return n->son[whichside]->sonw;
}

//查询num的排名
int getRank(int num) {
    find(num);
    return root->sonw-getChildCnt(root,1)-root->dupcnt+1;
}

//查找第k大的数
int getNum(int k) {
    node *cur=root;
    while(true) {
        //k比左子树的大小还小，说明第k大数在左子树里
        if(cur->lfs()!=NULL && k<=cur->lfs()->sonw) cur=cur->lfs();
        //k比左子树+自己的重复次数还大，说明在右子树里
        else if(k > getChildCnt(cur,0) + cur->dupcnt) {
            k-=getChildCnt(cur,0) + cur->dupcnt;
            cur=cur->rts();
        } else {//都不是，那就找到了
            return cur->value;
        }
    }
}

其他操作
除此之外，splay还可以实现区间翻转等操作，由于实用性不大(而且我不会)所以就不加以讨论。

 

最后放上完整代码

#include
#include
#include
#include
using namespace std;

struct node{
    public:
    node *son[2];
    node *father;
    int value;
    int dupcnt;
    int sonw;

    node(){
        father=son[0]=son[1]=NULL;
        value=dupcnt=sonw=0;
    }

    //left=0 right=1
    inline bool whichson(){
        if(father==NULL)return 0;
        return father->rts()==this;
    }

    inline node* lfs(){
        return son[0];
    }

    inline node* rts(){
        return son[1];
    }

    inline void update(){
        sonw=(lfs()!=NULL?lfs()->sonw:0)+(rts()!=NULL?rts()->sonw:0)+dupcnt;
    }

    void clearSon(){
        if(son[0]!=NULL)son[0]->clearSon(),delete son[0];
        if(son[1]!=NULL)son[1]->clearSon(),delete son[1];
    }
};

struct SplayTree{
    public:
    node *root;

    SplayTree(){
        root=NULL;
    }

    ~SplayTree(){
        if(root!=NULL)root->clearSon();
    }

    node* createNode(int val){
        node *n=new node();
        n->value=val;
        n->dupcnt++;
        return n;
    }

    void link(node *from,node *newfa,int whichside){
        if(newfa!=NULL)newfa->son[whichside]=from;
        if(from!=NULL)from->father=newfa;
    }

    void rotate(node *n){
        if(n==root)return;
        node *fa=n->father;
        node *grf=fa->father;
        int whichside=n->whichson();
        int fawh=fa->whichson();
        link(n->son[whichside^1],fa,whichside);
        link(fa,n,whichside^1);
        link(n,grf,fawh);
        fa->update();n->update();
    }

    void splay(node *sp,node *target=NULL){
        while(sp->father!=target){
            node *fa=sp->father;
            node *grf=fa->father;
            if(grf!=target){
                if(sp->whichson()==fa->whichson())rotate(fa);
                else rotate(sp);
            }
            rotate(sp);
        }
        if(target==NULL)root=sp;
    }

    node* chooseSon(node *n,int val){
        if(n->value>val)return n->son[0];
        else return n->son[1];
    }

    void find(int val){
        if(root==NULL)return;
        node *cur=root;
        while(chooseSon(cur,val)!=NULL&&cur->value!=val){
            cur=chooseSon(cur,val);
        }
        splay(cur);
    }

    void insertNode(int val){
        if(root==NULL){
            root=createNode(val);
            root->update();
            return;
        }
        node *cur=root;
        while(chooseSon(cur,val)!=NULL&&cur->value!=val){
            cur=chooseSon(cur,val);
        }
        if(cur->value==val){
            cur->dupcnt++;
            splay(cur);
            return;
        }
        int bw=val>(cur->value);
        node *c=createNode(val);
        link(c,cur,bw);
        splay(c);
    }

    void _delN(node *n){
        if(n->dupcnt>1){
            n->dupcnt--;
            n->update();
        }else{
            if(n==root){
                delete root;
                root=NULL;
            }else{
                n->father->son[n->whichson()]=NULL;
                n->father->update();
                delete n;
            }
        }
    }

    void deleteNode(int val){
        node *pre=getPre(val);
        node *post=getPost(val);
        if(pre->value==val&&post->value==val){
            _delN(root);
            return;
        }
        if(pre->value==val){
            splay(post);_delN(pre);
            return;
        }
        if(post->value==val){
            splay(pre);_delN(post);
            return;
        }
        splay(pre);
        splay(post,pre);
        _delN(post->lfs());
    }

    node* getPre(int val){
        find(val);
        if(root->valuelfs();
        if(cur==NULL)return root;
        while(cur->rts()!=NULL)cur=cur->rts();
        return cur;
    }

    node* getPost(int val){
        find(val);
        if(root->value>val)return root;
        node *cur=root->rts();
        if(cur==NULL)return root;
        while(cur->lfs()!=NULL)cur=cur->lfs();
        return cur;
    }

    int getRank(int num){
        find(num);
        return root->sonw-getChildCnt(root,1)-root->dupcnt+1;
    }

    int getChildCnt(node *n,int whichside){
        if(n->son[whichside]==NULL)return 0;
        return n->son[whichside]->sonw;
    }

    int getNum(int k){
        node *cur=root;
        while(true){
            if(cur->lfs()!=NULL&&k<=cur->lfs()->sonw)cur=cur->lfs();
            else if(k>getChildCnt(cur,0)+cur->dupcnt){
                k-=getChildCnt(cur,0)+cur->dupcnt;
                cur=cur->rts();
            }else{
                return cur->value;
            }
        }
    }
};


int n;
SplayTree ST;
int main(){
    cin>>n;
    while(n--){
        int op,x;
        cin>>op>>x;
        switch(op){
            case 1:{ST.insertNode(x);break;}
            case 2:{ST.deleteNode(x);break;}
            case 3:{cout<value<value<

洛谷评测

 

关于空间的优化
      每次新建结点时都要new一个对象，这样做是非常消耗时间的，所以我们可以建立一个类似对象池的东西，一次性分配一定量的内存，这样就可以避免频繁的空间申请和释放。

typedef node* nodeptr;
struct NodePool{
    nodeptr pool;
    nodeptr *allocatedPtr;
    int allocatedCount;

    NodePool(int maxn){
        //malloc
        //init
    }

    node *allocNode(){
        //...
    }

    void recycle(){
        //...
    }
};

事实证明，在SplayTree里应用以上框架实现的对象池可以得到20%左右的性能提升。