内部排序(三)堆排序的两种实现
堆排序是一种选择排序算法,堆排序顾名思义要用到堆,首先来回顾下有关数据结构“堆”有哪些特点。
- 堆常用二叉树来表示,而且如果不是特殊情况的话,通常用一棵完全二叉树来表示堆。因为完全二叉树的结点分布均匀,所以通常可以用数组来实现堆的存储。
- 根据堆中任一结点和其他结点的值的关系,堆分成两种,最大堆和最小堆。最大堆指堆中任一结点的值都大于其子结点的值;最小堆则相反,堆中任一结点的值都小于其子结点的值。
看到堆的特点之后,是不是冥冥之中觉得这种任一结点比其子结点大/小的特性或许可以用来做排序?对的,堆排序是选择排序的一种,选择排序大家很容易理解,一种“暴力”的选择排序方法就是每次扫描一遍整个待排序列,从中找出最大/最小值,然后保存到一个额外空间中,接着再把待排序列剩下的元素每个扫描一遍,再从中找出最大/最小的元素,这样一直下去直到把待排序列所有元素“清空”。
但是我们知道每一都扫描一遍整个待排序列来找出最大/最小元素,肯定是不合适的。那么我们想如何可以加快寻找最大值/最小值这一步骤?
那就是用最大堆或最小堆了!因为最大堆的根结点一定就是存放的最大元素,最小堆的根结点一定就是存放的最小元素。所以就可以利用最大堆/最小堆来快速获取待排序列中的最值,从而加快排序的速度!这就是堆排序。
那么如何做堆排序呢?假设我们要对序列做升序排序(降序同理),第一种方法,我们可以把待排序列中元素一个一个拿出来建成一个最大堆,这样每次从最大堆从弹出一个最大元素,然后按升序方式放回我们的待排序列中,就可以了。这样真的是可以,实现代码如下:
/*主函数*/
int main(int agrc, char const* argv[])
{
bool IsFull, IsEmpty;
int i, j;
ElemType InsertData, DeleteItem, data=0;
/*创建一个堆序列,把待排序列一个一个插入到堆中并调整成最大堆*/
PtrlSqList H=CreatList();
/*创建一个待排序列*/
PtrlSqList P=CreatList();
printf("请创建待排序列:");
while (data!=-1) {
scanf("%d", &data);
if (data!=-1) {
Insert_Array(P, data);
}
}
/*获得待排序列长度*/
P->length=GetListLength(P);
/*输出待排序列*/
printf("\n待排序列为:");
PrintList(P, 0);
printf("\n待排序列长度=%d\n", P->length);
/*把待排序列元素一个个插入到堆中同时做调整*/
/*for循环中i<=P->length+1是为了把-1结束标志也存进去*/
for (i=1; i<=P->length+1; i++) {
Insert(H, P->arr[i]);
P->arr[i]=0;
j=i;
}
P->arr[j]=-1; /*结束符*/
printf("\n最大堆H:");
PrintList(H, 0);
/*获取最大堆的长度*/
H->length=GetListLength(H);
printf("\n最大堆H的长度=%d\n", H->length);
printf("\n回归过程:\n");
j=P->length;
for (i=1; i<=P->length; i++) {
P->arr[j]=Delete(H);
PrintList(P, 0);
printf("\n");
j--;
}
printf("\n堆排序后序列:");
PrintList(P, 0);
return 0;
} 创建一个空堆H和待排序列P,第55行开始for循环把待排序列P中的元素一个一个拿出来插入到堆H中同时每次插入后都调整堆H为最大堆。把待排序列全部插入调整成一个最大堆后,就可以开始从最大堆不断弹出堆顶元素,按需要的排序方式存放回序列P中:
如何在插入一个元素到堆中后同时把堆调整成最大堆?我们来看代码:
/*判断最大堆是否已满*/
bool IsFull(PtrlSqList P)
{
return (P->MaxContent==P->NowSize);
}
/*判断最大堆是否为空*/
bool IsEmpty(PtrlSqList P)
{
return (P->NowSize==0);
}
/*最大堆的插入*/
void Insert(PtrlSqList H, ElemType X)
{
int i;
/*插入前先判断堆满不满*/
if (IsFull(H)) {
printf("最大堆已满,无法插入.");
return;
}
/*没有满就插入*/
i=++H->NowSize; /*因为NowSize记录的是当前堆中最后一个元素的下标,所以在它后面做插入*/
/*调整插入的位置,如果i位置的父结点比插入的值小,就把父结点移动下来*/
/*i/2是i的父结点,2i是左子树,2i+1是右子树*/
for (; H->arr[i/2]arr[i]=H->arr[i/2]; /*把父结点往下移*/
}
/*i的父结点不比要插入的X小了,那么就插入X到i*/
H->arr[i]=X;
} 第162行插入元素前首先判断堆满不满,没满就让i=++H->NowSize。然后开始找插入的位置,第170行从当前堆中最后一个位置的父结点开始,如果父结点的值比要插入的X小,那么就把父结点下移,让X到父结点的位置,父结点下移即把堆中父结点H->arr[ i/2 ]的值赋给H->arr[ i]位置的值。然后i\=2,就是从i的父结点继续往上找,直到找到父结点i比要插入的X大了,X就作为i的子结点插入。
至于在做完插入操作把待排序列建立成一个最大堆后,怎么把最大堆堆顶元素一个一个弹出来?这样实现:
/*最大堆的删除(即弹出一个元素)*/
ElemType Delete(PtrlSqList H)
{
int Head, Max; /*Head是要插入的位置, Max是Head的子结点的下标位置*/
ElemType DeleteItem, Tag;
/*弹出一个元素前,先判断堆为不为空*/
if (IsEmpty(H)) {
printf("最大堆为空.");
return;
}
/*不为空就弹出元素*/
DeleteItem=H->arr[1]; /*先把要弹出的结点保存起来,最后返回出去*/
Tag=H->arr[H->NowSize--]; /*保存弹出一个元素后,堆中最后一个元素(最小元素)的下标*/
/*下面的操作是把弹出一个元素后的堆调整回最大堆*/
/*Head*2是判断该结点是否有左子树,Head*2是左子树,Head*2+1是右子树*/
/*Head即要插入的位置从1开始,即从第一个顶点(根节点)开始判断*/
for (Head=1; Head*2<=H->NowSize; Head=Max) {
/*如果有左子树,就判断左子树和右子树谁更大*/
/*Head*2<=NowSize判断当前要插入的位置是否有左子树,如果左子树==NowSize,则没右子树*/
Max=Head*2; /*一开始先让Max的值是左子树的位置下标,即指向左子树*/
/*如果左子树结点小于右子树结点*/
if ((H->arr[Max]arr[Max+1]) && (Max!=H->NowSize)) {
/*Max!=H->NowSize,证明有右子树*/
/*就把Max指向更大的右子树的位置*/
Max++;
}
/*一轮循环找到当前要插入的位置的左右子树的更大的那个位置Max后*/
/*比较我当前要插入的元素Tag是否比左右子树大,是就直接插入*/
if (Tag>=H->arr[Max]) {
break;
} else {
/*否则就把更大的那个值提上来,调成最大堆的规律*/
/*而我Tag要插入的位置下移,下移操作是for循环的最后Head=Max*/
/*Head=Max即把Head的子树位置给了自己,让自己下移了*/
H->arr[Head]=H->arr[Max];
}
}
/*for循环做完后,即找到正确的插入位置,就插入Tag元素*/
H->arr[Head]=Tag;
return DeleteItem;
} 一样弹出元素前先判断堆空不空,不空就把堆顶元素H->arr[ 1 ]赋值给DeleteItem变量保存,最后返回出去。关键是弹出一个元素后,怎么把堆调整回最大堆。
第181行定义了两个变量Head和Max,Head是用来保存查找插入位置的,因为堆中弹出一个元素后,堆得大小就要-1,而堆的数据结构中NowSize是用来保存堆中当前的容量,值就是堆中最后一个元素的位置的下标,所以再弹出了一个元素后,第191行我们把堆中最后一个元素的值赋给Tag’变量暂时保持,NowSize--,然后为这个Tag元素找插入的位置,同时调整堆。
首先让Head=1就是从堆顶位置开始,如果Head*2<=H->NowSize,意思是判断该结点有没有左结点且有没有超出堆的大小,如果没有,就证明有左结点且有右结点(Head*2<=H->NowSize,小于NowSize很重要,因为左结点的位置下标是2i,右结点的位置下标是2i+1,所以如果左结点的下标没有超出NowSize,就证明有右结点)。
然后第199行先让Max指向左结点的位置,判断如果左结点小于右结点,就让Max指向右结点。这一步的做法是找出当前插入位置的子结点更大的结点,如果要插入的元素Tag比当前要插入的位置的子结点都大,如果是,就证明插入位置找到了,break停止循环,第220把Tag赋值给H->arr[ Head ]。如果Tag比插入位置Head的子结点要小,那么就把子结点Max的位置赋值给Head,即往下寻找插入位置。
上面这种堆排序的做法,其实也不适合,因为我们看排序部分的代码,我们需要一个额外的空间堆H来存待排序列的元素,把待排序列建立成一个最大堆。最后还有把排好序后的最大堆中元素一个一个复制回去原序列中,尤其是最后的复制回归过程,当数据量很大时,这个数据复制时间就可能要很久,而且需要的额外空间堆H也可能很大。
为了去掉额外空间和重新复制元素回原序列,可以用第二种更好的方法,就是直接对待排序列动手。方法是,首先我们直接把整个待排序列调整成最大堆形式,这时堆顶元素就是最大值,因为我们要把待排序列排成升序,升序序列中最大的元素是排在最后的(可按需要改动代码实现其他规律的排序),所以,我们把堆顶元素和堆中最后一个元素例如N做交换,接着把最后一个元素之前的堆调整回一个最大堆。然后对N-1的堆中元素继续把最大堆中第一个元素和最后一个元素,此时是N-1交换,这样序列中第二大的元素就去到了序列的倒数第二个位置了。
一直做下去,把堆调整回最大堆,然后把第一个元素和N-2的位置的元素交换,直到所有元素排完序,最后直接逐个弹出堆中所有元素回原序列P中即可,我们来看看代码,看看它是怎么回事:
/*堆排序*/
void Heap_Sort(PtrlSqList P)
{
int i=0;
/*从最后一个结点的父结点开始往上调整*/
for (i=P->length/2; i>0; i--) {
/*把待排序列中的元素调整成最大堆*/
AdjustMaxHeap(P, i, P->length);
}
/*调整成最大堆后的序列*/
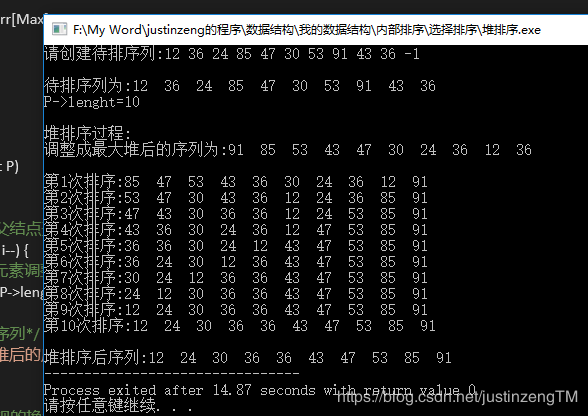
printf("调整成最大堆后的序列为:");
PrintList(P, 0);
printf("\n\n"); /*为了美观的换行*/
/*开始堆排序*/
for (i=P->length; i>0; i--) {
//printf("此时i=%d\n", i);
Swap(&P->arr[1], &P->arr[i]);
/*一趟堆排序后,把待排序列继续调整回最大堆,做下一趟堆排序*/
AdjustMaxHeap(P, 1, i-1);
PrintList(P, (P->length-i+1));
printf("\n");
}
}第144行把待排序列调整成最大堆,然后第156行for循环,从堆中最后一个元素的位置开始,即P->length,每次Swap函数是把堆中第一个元素和“最后一个”元素交换,交换完后,即最大元素落到最后一位了,就把之前的元素调整回最大堆。
Swap函数是用户自定函数,目的是实现两位置元素交换,比较简单且方法很多,这里就不展示了。
至于调整堆为最大堆函数AdjustMaxHead,我们来看怎么做:
/*调整堆的有序性,调整为最大堆*/
void AdjustMaxHeap(PtrlSqList P, ElemType i, int length)
{
int Head, Max; /*作用和最大堆删除函数中一样*/
ElemType Tmp; /*临时保存那个要调整位置的元素*/
Tmp=P->arr[i]; /*把要调整位置的元素赋给一个临时变量*/
for (Head=i; Head*2<=length; Head=Max) {
Max=Head*2;
if (Max!=length && P->arr[Max]arr[Max+1]) {
Max++;
}
if (Tmp>P->arr[Max]) {
break;
} else {
P->arr[Head]=P->arr[Max];
}
}
P->arr[Head]=Tmp;
} 方法和上面最大堆弹出一个元素调整位置一样,只是传入参数不同,最大堆的调整,因为我们每次排序都把最大元素放到最后的位置,交换了位置之后,堆中1的位置元素是当前待排序列最后一个元素,所以参数i是1,length是每次要调整的元素的个数。方法一模一样,从位置1开始,如果左右结点比Tmp大,就把要插入的位置Head下移(否则直接插入),直到找到比位置Head的子结点大后,在位置Head处插入。
方法2就不需要额外的空间来暂存数据,也就省掉了把排好序的数据复制回原序列中的这费时间一步。
完整实现代码在个人代码云:
https://gitee.com/justinzeng/codes/3cnvf7ktjqbzpoah95mwi62
https://gitee.com/justinzeng/codes/5aowfdl9v4y2n3i6jszek68