python keras LSTM 学习

本文源自https://machinelearningmastery.com/time-series-forecasting-long-short-term-memory-network-python/
参考http://blog.csdn.net/Goldxwang/article/details/76207831?locationNum=6&fps=1

from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from math import sqrt
from matplotlib import pyplot
import numpy as np
import pandas as pd
# load dataset
series = pd.read_csv('file:///E:/data/sales-of-shampoo-over-a-three-ye.csv', header=0, parse_dates=[0], index_col=0, squeeze=True)#date_parser=parser
#squeeze=True。如果文件值包含一列，则返回一个Series
series=series.dropna().rename('Sales')

# frame a sequence as a supervised learning problem
'''
将时间序列转化为监督学习
Keras中的LSTM模型假设您的数据分为两部分：输入（X）和输出（y）。
对于时间序列问题，我们可以将上一时间步（t-1）的观测值作为输入，将当前时间步（t）的观测值作为输出。
为了实现这一转化，我们可以调用Pandas库中的shift()函数将某一序列中的所有数值向下错位特定的位数。我们需要向下错一位，
这位上的数值将成为输入变量。该时间序列则将成为输入变量。
然后我们将这两个序列串在一起创建一个DataFrame进行监督学习。向下错位后的序列移到了顶部，
没有任何数值。此位置将使用一个NaN（非数）值。我们将用0值代替这些NaN值，LSTM 模型将不得不学习“序列的开头”或“此处无数据”，
因为此数据集中未观察到销量为零的月份。
下方的代码定义了一个完成此步的辅助函数，名称为 timeseries_to_supervised()。
这个函数由原始时间序列数据的NumPy数组和一个滞后观察值或错位的序列数生成，并作为输入使用。
'''
def timeseries_to_supervised(data, lag=1):
    df = pd.DataFrame(data)
    columns = [df.shift(i) for i in range(1, lag+1)]
    columns.append(df)
    df = pd.concat(columns, axis=1)
    df.fillna(0, inplace=True)
    return df

# transform to supervised learning
X = series.values
supervised = timeseries_to_supervised(X, 1)
supervised.head()


# create a differenced series
'''
将时间序列转化为静态
洗发水销量数据集不是静止的。
这意味着数据中的某个结构与时间有关。更确切地说，数据中存在增加的趋势。
静态数据更容易建模，并且很可能得出更加准确的预测。
可以从观察中移除该趋势，然后再添加至预测中，将预测恢复至原始区间并计算出相当的误差值。
移除趋势的标准方法是差分数据。也就是从当前观察值（t）中减去从上一时间步（t-1）得到的观察值。
这样我们就移除了该趋势，得到一个差分序列，或者一个时间步及其下一时间步得出的观察值发生改变。
我们可以通过调用pandas库中的diff() function函数自动完成此步。
另外，我们还可以获得更好的控制，用我们自己编写的函数完成此步，在该例中我们将采用这种方法，因为它具有灵活性。
下方是一个名称为difference()的函数，用来计算差分序列。注意，由于不存在用于计算差分值的先前观察值，因此须略过该序列中的第一个观察值。
'''
def difference(dataset, interval=1):
    diff = list()
    for i in range(interval, len(dataset)):
        value = dataset[i] - dataset[i - interval]
        diff.append(value)
    return pd.Series(diff)

# invert differenced value
'''
为了使差分序列的预测恢复至原始的区间内，我们还需要逆转这个流程。
下方的这个名为inverse_difference()的函数用来逆转这个操作。
我们可以通过差分整个序列来测试这些函数，然后再将它恢复至原始区间内
'''
def inverse_difference(history, yhat, interval=1):
    return yhat + history[-interval]

# scale train and test data to [-1, 1]
'''
转化时间序列使其处于特定区间
和其他神经网络一样，LSTM要求数据须处在该网络使用的激活函数的区间内。
LSTM的默认激活函数为双曲正切函数（tanh），这种函数的输出值处在-1和1之间，这也是时间序列函数的区间。
为了保证该试验的公平，缩放系数（最小和最大）值必须根据训练数据集计算，并且用来缩放测试数据集和任何预测。
这是为了避免该实验的公平性受到测试数据集信息影响，而可能使模型在预测时处于劣势。
我们可以使用MinMaxScaler class转化数据集使其处在 [-1, 1] 区间内。
和其他scikit-learn转换模块一样，它需要提供行列矩阵形式的数据。因此，我们必须在转换数据集之前变换NumPy数组。
'''
# transform scale
X = series.values
X = X.reshape(len(X), 1)

scaler = MinMaxScaler(feature_range=(-1, 1))#建模
scaler = scaler.fit(X)#训练
scaled_X = scaler.transform(X)#转化
#scaled_X.head()
scaled_series = pd.Series(scaled_X[:, 0])#转换类型成序列
print(scaled_series.head())
# invert transform还原
inverted_X = scaler.inverse_transform(scaled_X)
inverted_series = pd.Series(inverted_X[:, 0])
print(inverted_series.head())

#上述操作写成函数
def scale(train, test):
    # fit scaler
    scaler = MinMaxScaler(feature_range=(-1, 1))
    scaler = scaler.fit(train)
    # transform train
    train = train.reshape(train.shape[0], train.shape[1])
    train_scaled = scaler.transform(train)
    # transform test
    test = test.reshape(test.shape[0], test.shape[1])
    test_scaled = scaler.transform(test)
    return scaler, train_scaled, test_scaled

 # inverse scaling for a forecasted value
def invert_scale(scaler, X, value):
    new_row = [x for x in X] + [value]
    array = np.array(new_row)
    array = array.reshape(1, len(array))
    inverted = scaler.inverse_transform(array)
    return inverted[0, -1]


# fit an LSTM network to training data

model = Sequential()
model.add(LSTM(neurons, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True))
#LSTM层必须使用 “batch_input_shape” 语句作为元组定义输入数据的形态，该语句详细规定读取没批数据的预期观察值数，时间步数和特征数。
#batch大小通常要比样本总数小很多。它和epoch的数目共同决定网络学习数据的速度（权值更新的频率）。
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
#在编译网络时，我们必须规定一个损失函数和优化算法。
#我们将使用“mean_squared_error”作为损失函数，因为它与我们要计算的平方根误差十分接近，使用高效的ADAM优化算法。


def fit_lstm(train, batch_size, nb_epoch, neurons):
    X, y = train[:, 0:-1], train[:, -1]
    X = X.reshape(X.shape[0], 1, X.shape[1])
    model = Sequential()
    model.add(LSTM(neurons, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True))
    model.add(Dense(1))
    model.compile(loss='mean_squared_error', optimizer='adam')
    for i in range(nb_epoch):
        model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)
#在默认下，epoch内的样本在输入网络之前已经混合。同样，这对LSTM而言很不理想，因为我们希望该网络通过学习观察值序列形成状态。我们通过设置“shuffle”为“False”来禁止样本的混合
#默认下，该网络在每个epoch结束时报告大量关于学习进展和模型技能的调试信息。我们可以将“verbose”语句设置为“0”级别以禁止该报告。
        model.reset_states()
#一个 batch = 来自训练数据的确定个数的 rows , 他确定了在更新整个网络权重前需要处理的 pattern 的个数
#默认的，batchs 间的状态会清空，通过调用 reset_states() 可以控制什么时候清除 LSTM 层状态
    return model

def forecast(model, batch_size, row):
    X = row[0:-1]
    X = X.reshape(1, 1, len(X))
    yhat = model.predict(X, batch_size=batch_size)
    return yhat[0,0]


# date-time parsing function for loading the dataset
def parser(x):
    return datetime.strptime('190'+x, '%Y-%m')

# frame a sequence as a supervised learning problem
def timeseries_to_supervised(data, lag=1):
    df = DataFrame(data)
    columns = [df.shift(i) for i in range(1, lag+1)]
    columns.append(df)
    df = concat(columns, axis=1)
    df.fillna(0, inplace=True)
    return df

# create a differenced series
def difference(dataset, interval=1):
    diff = list()
    for i in range(interval, len(dataset)):
        value = dataset[i] - dataset[i - interval]
        diff.append(value)
    return Series(diff)

# invert differenced value
def inverse_difference(history, yhat, interval=1):
    return yhat + history[-interval]

# scale train and test data to [-1, 1]
def scale(train, test):
    # fit scaler
    scaler = MinMaxScaler(feature_range=(-1, 1))
    scaler = scaler.fit(train)
    # transform train
    train = train.reshape(train.shape[0], train.shape[1])
    train_scaled = scaler.transform(train)
    # transform test
    test = test.reshape(test.shape[0], test.shape[1])
    test_scaled = scaler.transform(test)
    return scaler, train_scaled, test_scaled

# inverse scaling for a forecasted value
def invert_scale(scaler, X, value):
    new_row = [x for x in X] + [value]
    array = numpy.array(new_row)
    array = array.reshape(1, len(array))
    inverted = scaler.inverse_transform(array)
    return inverted[0, -1]

# fit an LSTM network to training data
def fit_lstm(train, batch_size, nb_epoch, neurons):
    X, y = train[:, 0:-1], train[:, -1]
    X = X.reshape(X.shape[0], 1, X.shape[1])
    model = Sequential()
    model.add(LSTM(neurons, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True))
    model.add(Dense(1))
    model.compile(loss='mean_squared_error', optimizer='adam')
    for i in range(nb_epoch):
        model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)
        model.reset_states()
    return model

# make a one-step forecast
def forecast_lstm(model, batch_size, X):
    X = X.reshape(1, 1, len(X))
    yhat = model.predict(X, batch_size=batch_size)
    return yhat[0,0]

上述代码只是为了理解整个lstm的操作过程，实际工作中需要多步预测Multi-Step

原文https://machinelearningmastery.com/multi-step-time-series-forecasting-long-short-term-memory-networks-python/
以下代码为多步预测的完整代码

from pandas import DataFrame  
from pandas import Series  
from pandas import concat  
from pandas import read_csv  
from pandas import datetime  
from sklearn.metrics import mean_squared_error  
from sklearn.preprocessing import MinMaxScaler  
from keras.models import Sequential  
from keras.layers import Dense  
from keras.layers import LSTM  
from math import sqrt  
from matplotlib import pyplot  
from numpy import array  

# date-time parsing function for loading the dataset  
def parser(x):  
    return datetime.strptime('190'+x, '%Y-%m')  

# convert time series into supervised learning problem  
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):  
    n_vars = 1 if type(data) is list else data.shape[1]  
    df = DataFrame(data)  
    cols, names = list(), list()  
    # input sequence (t-n, ... t-1)  
    for i in range(n_in, 0, -1):  
        cols.append(df.shift(i))  
        names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]  
    # forecast sequence (t, t+1, ... t+n)  
    for i in range(0, n_out):  
        cols.append(df.shift(-i))  
        if i == 0:  
            names += [('var%d(t)' % (j+1)) for j in range(n_vars)]  
        else:  
            names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]  
    # put it all together  
    agg = concat(cols, axis=1)  
    agg.columns = names  
    # drop rows with NaN values  
    if dropnan:  
        agg.dropna(inplace=True)  
    return agg  

# create a differenced series  
def difference(dataset, interval=1):  
    diff = list()  
    for i in range(interval, len(dataset)):  
        value = dataset[i] - dataset[i - interval]  
        diff.append(value)  
    return Series(diff)  

# transform series into train and test sets for supervised learning  
#转化
def prepare_data(series, n_test, n_lag, n_seq):  
    # extract raw values  
    raw_values = series.values  
    # transform data to be stationary  
    diff_series = difference(raw_values, 1)  
    diff_values = diff_series.values  
    diff_values = diff_values.reshape(len(diff_values), 1)  
    # rescale values to -1, 1  
    scaler = MinMaxScaler(feature_range=(-1, 1))  
    scaled_values = scaler.fit_transform(diff_values)  
    scaled_values = scaled_values.reshape(len(scaled_values), 1)  
    # transform into supervised learning problem X, y  
    supervised = series_to_supervised(scaled_values, n_lag, n_seq)  
    supervised_values = supervised.values  
    # split into train and test sets  
    train, test = supervised_values[0:-n_test], supervised_values[-n_test:]  
    return scaler, train, test  

# fit an LSTM network to training data  
def fit_lstm(train, n_lag, n_seq, n_batch, nb_epoch, n_neurons):  
    # reshape training into [samples, timesteps, features]  
    X, y = train[:, 0:n_lag], train[:, n_lag:]  
    X = X.reshape(X.shape[0], 1, X.shape[1])  
    # design network  
    model = Sequential()  
    model.add(LSTM(n_neurons, batch_input_shape=(n_batch, X.shape[1], X.shape[2]), stateful=True))  
    model.add(Dense(y.shape[1]))  
    model.compile(loss='mean_squared_error', optimizer='adam')  
    # fit network  
    for i in range(nb_epoch):  
        model.fit(X, y, epochs=1, batch_size=n_batch, verbose=0, shuffle=False)  
        model.reset_states()  
    return model  

# make one forecast with an LSTM,  
def forecast_lstm(model, X, n_batch):  
    # reshape input pattern to [samples, timesteps, features]  
    X = X.reshape(1, 1, len(X))  
    # make forecast  
    forecast = model.predict(X, batch_size=n_batch)  
    # convert to array  
    return [x for x in forecast[0, :]]  

# evaluate the persistence model  
def make_forecasts(model, n_batch, train, test, n_lag, n_seq):  
    forecasts = list()  
    for i in range(len(test)):  
        X, y = test[i, 0:n_lag], test[i, n_lag:]  
        # make forecast  
        forecast = forecast_lstm(model, X, n_batch)  
        # store the forecast  
        forecasts.append(forecast)  
    return forecasts  

# invert differenced forecast  
def inverse_difference(last_ob, forecast):  
    # invert first forecast  
    inverted = list()  
    inverted.append(forecast[0] + last_ob)  
    # propagate difference forecast using inverted first value  
    for i in range(1, len(forecast)):  
        inverted.append(forecast[i] + inverted[i-1])  
    return inverted  

# inverse data transform on forecasts  
def inverse_transform(series, forecasts, scaler, n_test):  
    inverted = list()  
    for i in range(len(forecasts)):  
        # create array from forecast  
        forecast = array(forecasts[i])  
        forecast = forecast.reshape(1, len(forecast))  
        # invert scaling  
        inv_scale = scaler.inverse_transform(forecast)  
        inv_scale = inv_scale[0, :]  
        # invert differencing  
        index = len(series) - n_test + i - 1  
        last_ob = series.values[index]  
        inv_diff = inverse_difference(last_ob, inv_scale)  
        # store  
        inverted.append(inv_diff)  
    return inverted  

# evaluate the RMSE for each forecast time step  
def evaluate_forecasts(test, forecasts, n_lag, n_seq):  
    for i in range(n_seq):  
        actual = [row[i] for row in test]  
        predicted = [forecast[i] for forecast in forecasts]  
        rmse = sqrt(mean_squared_error(actual, predicted))  
        print('t+%d RMSE: %f' % ((i+1), rmse))  

# plot the forecasts in the context of the original dataset  
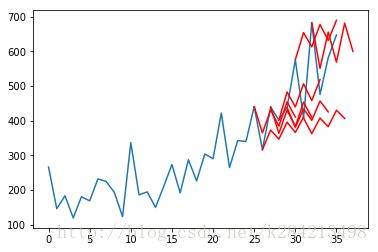
def plot_forecasts(series, forecasts, n_test):  
    # plot the entire dataset in blue  
    pyplot.plot(series.values)  
    # plot the forecasts in red  
    for i in range(len(forecasts)):  
        off_s = len(series) - n_test + i - 1  
        off_e = off_s + len(forecasts[i]) + 1  
        xaxis = [x for x in range(off_s, off_e)]  
        yaxis = [series.values[off_s]] + forecasts[i]  
        pyplot.plot(xaxis, yaxis, color='red')  
    # show the plot  
    pyplot.show()  

# load dataset  
series = read_csv('file:///E:/data/sales-of-shampoo-over-a-three-ye.csv', header=0, parse_dates=[0], index_col=0, squeeze=True)#date_parser=parser
series=series.dropna().rename('Sales')
# configure  
#一步数据，预测3步
n_lag = 1  #timesteps
n_seq = 10  #features
n_test = 3  #给了最后12个月，预测3个月，则能预测的次数是10，即10个3个月。12-10=2,2+1=3；12-4=8;
n_epochs = 1500  
n_batch = 1  
n_neurons = 1  
# prepare data  
scaler, train, test = prepare_data(series, n_test, n_lag, n_seq)  
# fit model  
model = fit_lstm(train, n_lag, n_seq, n_batch, n_epochs, n_neurons)  
# make forecasts  
forecasts = make_forecasts(model, n_batch, train, test, n_lag, n_seq)  
# inverse transform forecasts and test  
forecasts = inverse_transform(series, forecasts, scaler, n_test+2)  
actual = [row[n_lag:] for row in test]  
actual = inverse_transform(series, actual, scaler, n_test+2)  
# evaluate forecasts  
evaluate_forecasts(actual, forecasts, n_lag, n_seq)  
# plot forecasts  
plot_forecasts(series, forecasts, n_test+2)  

可以看到，其实效果挺一般，还有很多可改进的空间留待学习