大吉大利，今晚如何用R语言解锁“吃鸡”正确姿势

作者：钱诚  四川大学在读研究生

  

摘要

本文章通过《绝地求生》的部分游戏数据，探索该游戏特性和玩家偏好。在数据预处理后，对数据集进行以下几个方面的统计分析。首先通过对data1中“游戏开始时间”进行时间序列分析，探究PUBG玩家在游戏时间上的偏好；第二，对data2中角色死亡位置数据进行分析，以每场游戏开始时角色的死亡位置模拟玩家跳伞的位置，以每场游戏末尾角色的死亡位置模拟毒圈最后的刷新位置，探究玩家跳伞的偏好和毒圈收缩点的规律；第三，通过不同的武器枪械对data2进行划分，探究不同枪械的使用热度、击杀距离和使用位置等特征；第四，基于data1对不同类别的玩家进行生存分析，探究不同因子（是否驾车、是否团队作战等）对玩家生存时间的影响；第五，以玩家最终排名为因变量分别拟合多元线性回归模型和Logit回归模型，探索玩家成绩与哪些因素有关，以及关联程度如何。

目录

1.问题简介

2.数据来源及预处理      

    2.1数据描述     

    2.2数据预处理 

3.探索性分析    

    3.1玩家游戏时间偏好   

    3.2跳伞位置偏好    

    3.3毒圈最后位置    

    3.4枪械特征     

        3.4.1热度排名  

        3.4.2击杀距离  

        3.4.3使用位置  

    3.5生存分析     

        3.5.1队伍规模  

        3.5.2驾驶载具  

    3.6多元回归     

        3.6.1线性回归  

        3.6.2Logit回归  

参考资料    

代码附录    

01▶

问题简介

  《绝地求生》（PLAYERUNKNOWN’S BATTLEGROUNDS，后文简称PUBG）是一款战术竞技类的射击型沙盒游戏，其游戏模式为“大逃杀”类型，即每场游戏都会将一部分（标准情况下100人）玩家模拟空降至一个封闭的环境，经过战斗后最终幸存的玩家或队伍才算获得该场游戏的胜利。PUGB于2017年3月正式发行，由于设计精良、互动感强，上线以来迅速席卷了全球各国，成为热度最高的几款游戏之一。

       同时，庞大的地图和丰富的作战机制使得游戏结果具有很强的多样性，也产生了庞大的游戏和战斗数据。本报告试图根据PUBG开放的部分数据，对游戏特性和玩家偏好进行探索和分析。

02▶

数据来源及预处理

2.1数据描述

       本数据集来自于kaggle（点击阅读原文），含有数据集1和2两个部分。数据集1为场次数据，每场游戏中的每个玩家都会生成一个观测，描述该玩家某场游戏的一些总结性信息，如开场时间、游戏模式、玩家队伍最终排名等，一场N人参加的游戏会生成N条观测。数据集2为角色死亡记录，每场游戏中每一次角色死亡都会产生一条观测，该数据包括击杀所使用的武器信息、击杀者和被击杀者的游戏内坐标、死亡时间等信息，一场N人参加的游戏会产生N-k条数据，其中k为最终队伍胜利时所存活的人数。变量具体情况如表1表2所示：

表1 数据集1：场次数据

表2 数据集2：角色死亡记录

2.2数据预处理

       原始数据集包括数据集1和数据集2各约6千万条观测，如果全部运用则运算的时间成本过高。本报告并不侧重于机器学习与建模，不需要海量数据，因此对原始数据进行随机抽样，在两个数据集中分别抽取10万条观测进行后续统计分析，并分别命名为data1和data2。

       导入数据后，去除含有缺失值的观测，修改或删除部分异常值后，data1没有损失，data2剩余90,179条观测。同时，由于data1中的match_mode变量只有一个取值 “TPP”（第三人称视角），因此将此变量作为多余变量删除。

       经过统计，数据预处理后，data1包括96,640名玩家的72,801场游戏中的基本数据，data2包括87,047名玩家在97,392场游戏中的死亡记录。

03▶

探索性分析

本部分将对预处理后的数据集进行以下几个方面的统计分析。

• 首先通过对data1中“游戏开始时间”进行时间序列分析，探究PUBG玩家在游戏时间上的偏好；

• 第二，对data2中角色死亡位置数据进行分析，以每场游戏开始时角色的死亡位置模拟玩家跳伞的位置，以每场游戏末尾角色的死亡位置模拟毒圈最后的刷新位置，探究玩家跳伞的偏好和毒圈收缩点的规律；

• 第三，通过不同的武器枪械对data2进行划分，探究不同枪械的使用热度、击杀距离和使用位置等特征；

• 第四，基于data1对不同类别的玩家进行生存分析，探究不同因子（是否驾车、是否团队作战等）对玩家生存时间的影响；

• 第五，以玩家最终排名为因变量分别拟合多元线性回归模型和Logit回归模型，探索玩家成绩与哪些因素有关，以及关联程度如何。

3.1玩家游戏时间偏好

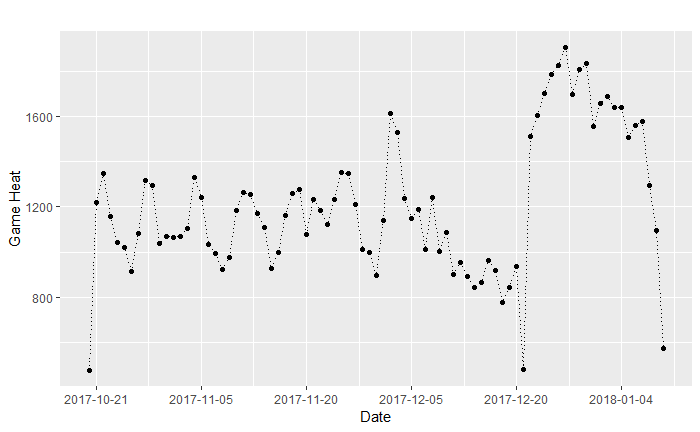
在R语言环境中，将data1中UTC格式字符串型的时间变量date经过字符串处理转化成YYYY-mm-dd-HH-MM-SS型时间变量。抽样所得到的数据发生在2017/10/20至2018/1/10之间，一共83天。统计每天发生游戏场数，据此绘制游戏热度变化趋势折线图，如图1所示：

             图1 游戏热度变化趋势

观测图1发现数据呈现有规律波动，首先对此数据进行移动平均平滑。简单观察图1，可能存在以星期为周期的波动，故取n=7进行移动平均，如图2所示：

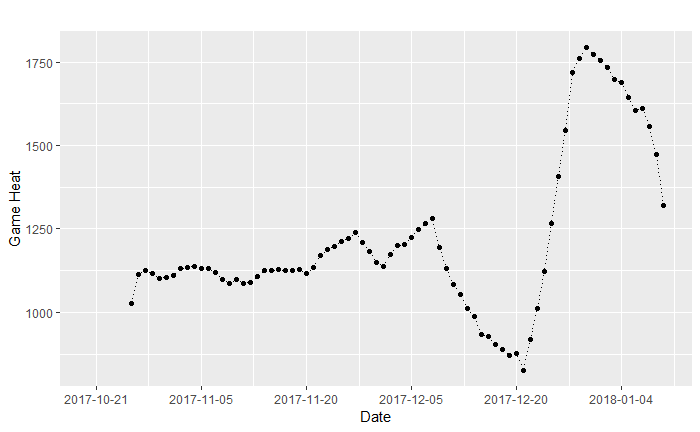
                图2 移动平均平滑（n=7）

 

       如图2所示，在全观测期内83天中，游戏热度整体上呈上升趋势，在12月10日至20日游戏热度发生了较大的衰退，这可能和2017年12月15日PUBG在微软Xbox One平台正式上线有关，部分玩家被暂时分流至其他服务器。随后进一步分解季节性趋势，如前所述以星期作为重复周期，结果如图3所示：

图3 按星期统计平均热度

 

       能明显看出周末的游戏热度高于工作日，特别是工作日的周三周四，是较为冷清的时期，游戏热度最低。

3.2跳伞位置偏好

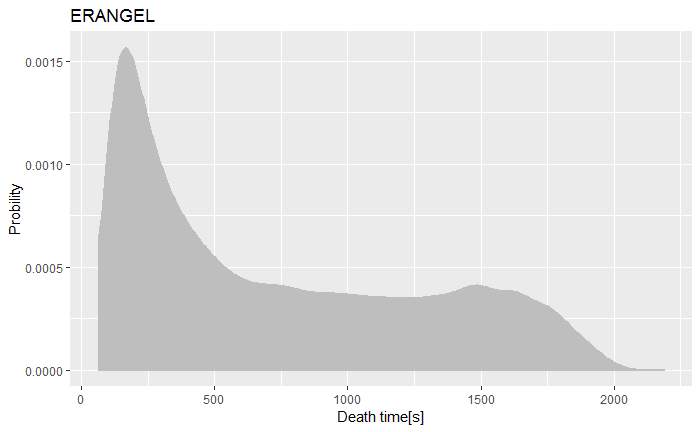
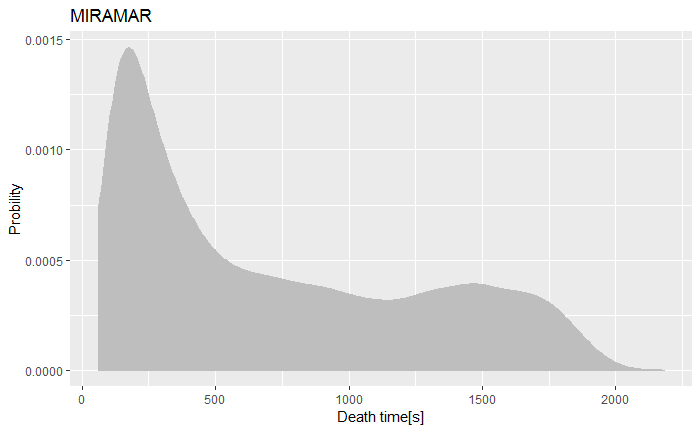
图4 角色死亡时间概率密度图

 

       统计游戏开场后角色死亡的时间点，概率密度分布如图4所示，两张地图的角色死亡时间分布高度相似。统计显示海岛地图和沙漠地图的角色死亡时间分布在65~2188s和62~2182s之间，峰值分别为129s和113s，即开场约1分钟后开始有玩家角色死亡，2分钟达到战斗/角色死亡的高发期。

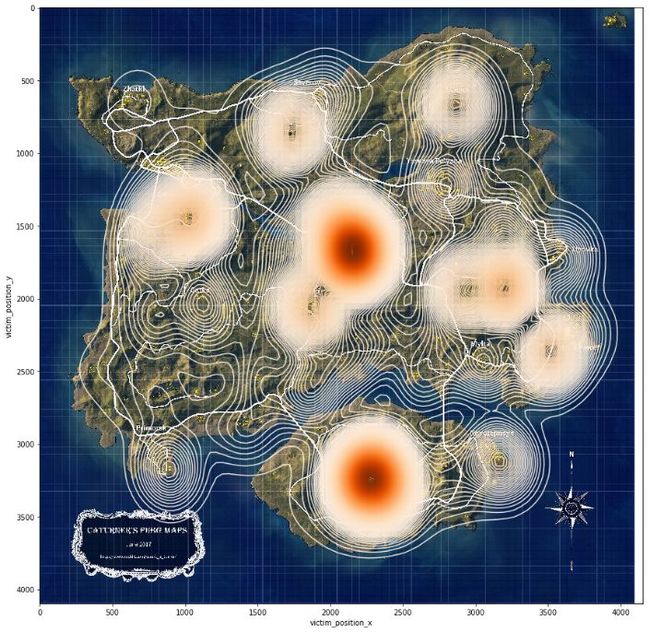
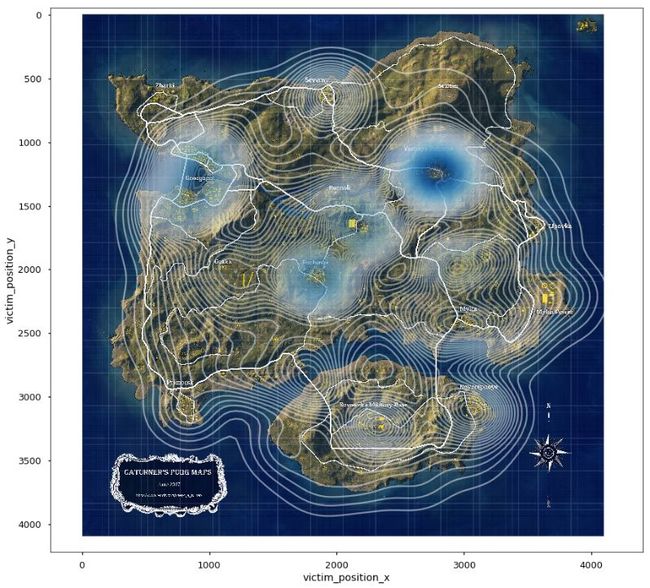
       选取两张地图自第1个玩家角色死亡开始60s内的死亡记录，根据坐标绘制热力图，即可模拟玩家在游戏开场后跳伞位置的选择偏好，如图5所示：

图5 跳伞点热力图

 

       由图5可以看出，ERANGEL海岛地图的玩家最主要的两个跳伞地区为P城和机场，这也是这张地图上资源最丰富的两个地点，除此外还有6个同样明显的跳伞热门地点。相比之下MIRAMAR沙漠地图的玩家跳伞显得更加集中，除了拳击场和别墅两处资源重地，其余地点的跳伞量都显得比较少，没有海岛地图中玩家的跳伞选择多样，这可能是由于MIRAMAR沙漠地图的资源刷新比较集中导致的。

3.3毒圈最后位置

PUBG为了加快游戏进度设定了“毒圈”机制，毒圈内为安全区，玩家在安全区外则会受到持续伤害。游戏开始后会出现越来越小的安全区，以此机制将所有玩家逼迫至同一地区决出胜负。本部分通过每场游戏末尾玩家角色死亡的坐标来模拟毒圈最后刷新地点的偏好。

根据PUBG官方公布的数据，最后两个毒圈的存续时间为195s，故选取最后死亡时间点逆推195s时间段内的数据，作出角色死亡地点相应的热力图，即可模拟最终毒圈的刷新位置偏好。由于最后195s时间段内死亡记录占比较少，在10万条抽样样本的情况下两张地图分别只得到65和13个观测，因此扩大抽样比例，在数据集2中重新抽取1000万条进行最终毒圈热力图的计算和绘制。

图6 最终安全区刷新热力图

 

对比图5和图6，可以发现热点地图有明显的错位，即最终安全区刷新频率较高的地区都不是跳伞热门地点。这或许反映了PUBG中毒圈动态刷新的一个重要原则：安全区往往会玩家少的地点刷新，以充分调动玩家的移动活跃性。

 

3.4枪械特征

本部分将角色死亡记录数据根据被击杀武器分为几个不同的部分，对各部分武器对应的击杀数据进行统计分析，以反映不同枪械的战斗特征。

3.4.1热度排名

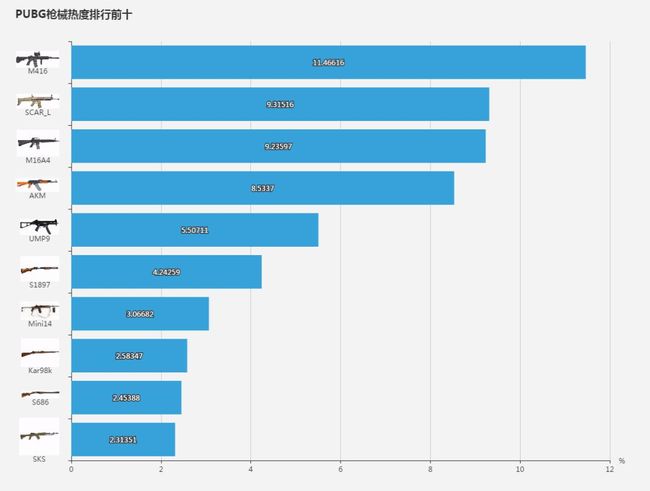
图7 枪械热度排名

 

       统计data2中各种武器使用的频次，换算成百分比进行排序，选取击杀敌人最多的10种枪械进行展示，结果如图7所示。这10种枪械可以分为步枪（M416/SCAR_L/M164A/AKM）、冲锋枪（UMP9）、狙击枪（Mini14/Kar98k/SKS）和霰弹枪（S1897/S686）四种。

• 步枪：射速较高、射程较远、弹容量大使得步枪有着均衡的性能，可以良好地应对近身火拼和远距离瞄准，是几乎每个玩家的必备品，在热度排名中牢牢占据前4名。这其中又分5.56mm小口径和7.62mm大口径步枪，5.56mm以其良好的操控性能和更轻便的弹匣更容易被玩家尤其是新手玩家选择，在排名中占据前三的位置。

• 冲锋枪：射速极高、后坐力小的特性使得冲锋枪在近距离作战中拥有超高的爆发伤害，但射程中等、弹道下坠严重等特性也使得冲锋枪只适合近距离作战。但冲锋枪当中的UMP9由于可扩展性良好（可加装瞄准镜、握把、弹匣和枪口），在有效射程上有不小的提升，是一把接近步枪性能的枪械，也受到玩家的喜爱，成为热度排行榜上仅次于步枪的存在。

• 霰弹枪：射程极短，只能用于近身作战，但一旦命中则伤害极高，是在游戏开场时大家短兵相接的情况下，非常好的选择之一。在冲锋枪UMP9随后就是同样常见的S1897霰弹枪。

• 狙击枪：射程极高，通常用于精准击杀远处敌人，需要配合高倍瞄准镜使用。相对与步枪、冲锋枪等，狙击枪的资源刷新量不高，往往要到游戏中后期玩家才能有机会得到，且使用难度较大，新手玩家很难熟练使用狙击枪击杀敌人。因此使用热度排列在较靠后的位置，如图中的Mini14和Kar98k。

3.4.2击杀距离

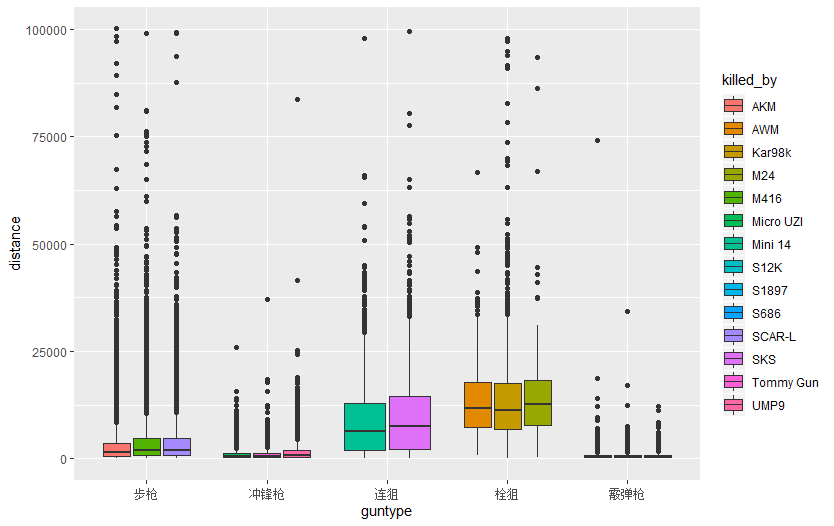
图8 不同种类枪械的击杀距离-箱线图

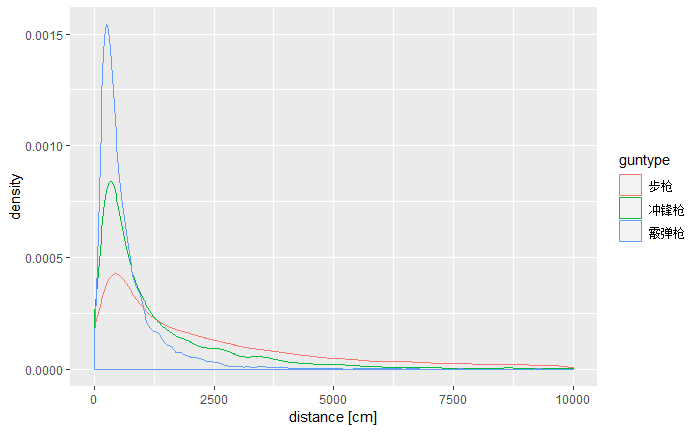
图9 不同种类枪械的击杀距离-密度图

       

进一步将狙击枪分类为栓狙和连狙两类，栓狙以Kar98k为代表，每进行一次射击后需要重新拉动枪栓才能进行下次射击；而连狙以SKS为代表，可以在一个弹匣的容量范围中连续进行射击，与步枪更为相似。栓狙的后坐力更高，射程更远，威力也更大，而连狙则为了兼顾射速而削弱了自身的射程和威力。

       本部分绘制了不同种类枪械击杀距离的箱线图和密度分布图，如图8和图9所示。在图8中可以清楚地看出，射击距离由近到远的排序分别为：霰弹枪——冲锋枪——步枪——连狙——栓狙，和各种枪械的特性非常吻合。图9中进一步展现了各种枪支击杀距离的详细分布，以步枪作为左右两张图的对照基准，左图中，冲锋枪和霰弹枪适合近距离战斗，但冲锋枪更接近步枪；右图中，连狙和栓狙更适合远距离战斗，但连狙要更接近步枪。

3.4.3使用位置

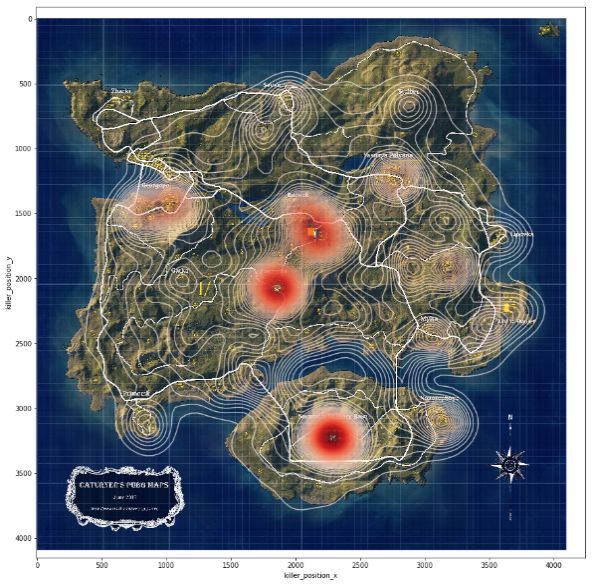
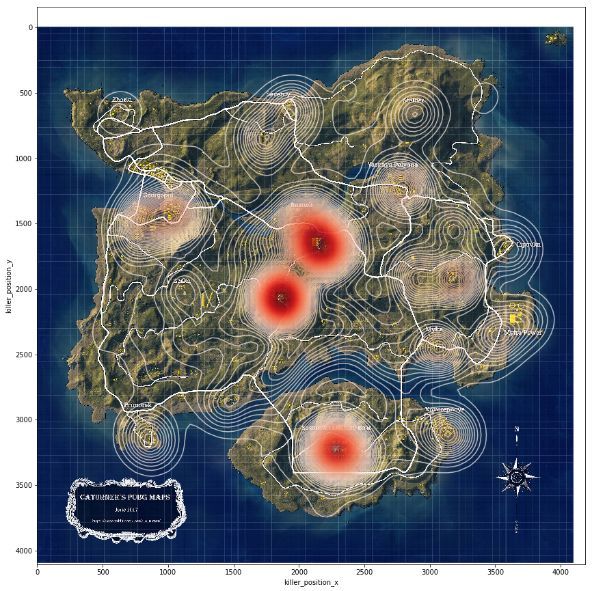
图11 步枪、冲锋枪、霰弹枪使用位置热力图

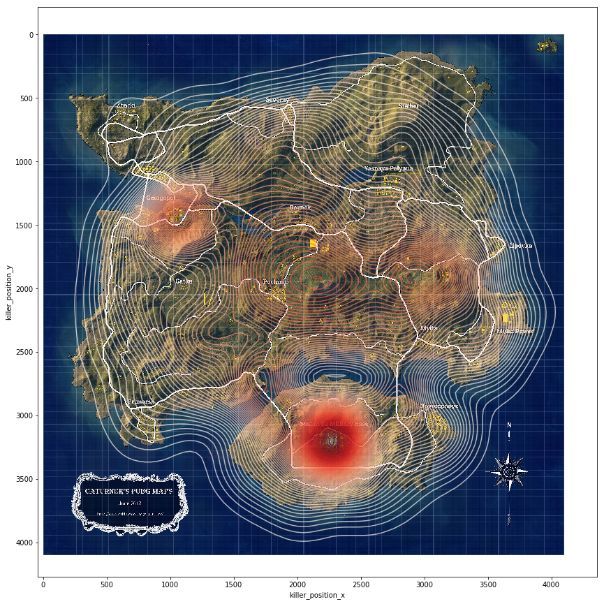
图12 连狙、栓狙使用位置热力图

 

       本部分分别绘制了五种枪械（步枪、冲锋枪、霰弹枪、连狙、栓狙）的使用位置热力图，如图11和图12所示。能明显看出，狙击枪的使用位置更加均匀和分散，不像其余枪支的使用更多地发生在建筑与城区等玩家密集的地点，这是可能是由于狙击枪拥有的良好的视野和远距离射程，在空旷地区更容易发现和击杀远处的敌人，还有可能是由于狙击枪（尤其是栓狙）的资源补给点比较分散。

3.5生存分析

     对data1中玩家生存时间建立生存分析模型，探究队伍规模和是否驾驶载具对玩家生存时间的影响。

3.5.1队伍规模

图13 队伍规模-玩家生存曲线

 

       从图13中能明显看出比赛队伍规模越大，在相同时间点玩家的生存率更高，这可能是由于多人游戏中相互配合和帮助的情况下，玩家在游戏内更为安全，也更不容易击杀敌人。同时可以看出，多人组队游戏中所有玩家的游戏总时间（与曲线下面积成正比）更长，即玩家总体上的参与度更高。

3.5.2驾驶载具

图14 驾驶载具-玩家生存曲线

 

       从图14能看出驾驶载具的情况下，相同时间点上玩家的生存率明显高于没有载具的情况。这可能是由于驾驶载具速度更快，更容易躲避敌人子弹或逃离战场，其次驾驶载具可以更轻易地进入安全区，远离毒圈的威胁。

3.6多元回归

       本小节将”team_placement”（玩家所在队伍最终排名）作为因变量，拟合多元回归模型，探究多种因素对玩家最终成绩的影响。本小节将分为两个部分，第一部分将该变量处理为连续变量时，拟合简单线性回归模型；第二部分将该变量处理为01变量（是否吃鸡），拟合Logit回归模型。

3.6.1线性回归

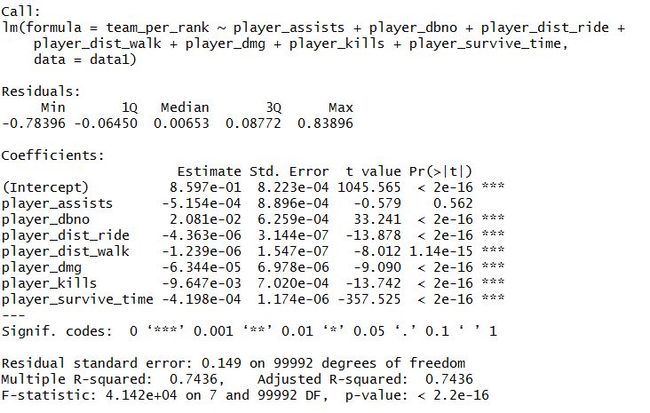
       本部分通过将玩家队伍最终排名作为因变量拟合多元线性回归模型，探究哪些因素和玩家最终成绩相关，相关程度如何。由于不同规模队伍的排名不能统一比较，故计算排名百分比变量“team_per_rank”，由队伍最终排名除以总队伍数量，表示队伍的成绩如何，该变量在0到1之间，值越小代表成绩越靠前。将排名成绩因变量与”player_assists”（救援队友次数）、”player_dbno”（玩家被击倒次数）等7个自变量拟合多元回归方程，在R语言环境下结果如下:

模型拟合结果显示，模型可以解释样本数据74.36%的方差，7个自变量中有6个都通过了t-test显著性检验。通过方差膨胀因子检验多重共线性，结果如下。

       

方差膨胀因子均小于10，可认为不存在严重的多重共线性问题。接下来将不显著的自变量“player_assists”（玩家救助人数）剔除，重新拟合模型，结果如下。

       拟合模型可以解释样本74.36%的方差，且所有变量均通过t-test显著性检验，自变量之间无严重多重共线性，故将此模型作为最终模型，表3列出了该模型所涉及的变量名及含义。方程如式（1）所示。

表3 方程（1）所涉及变量

方程因变量为”玩家成绩指标“，数值在0-1之间，表示在本次游戏中取得了前百分之多少的成绩，该变量越小代表玩家成绩越好。由该方程可以看出，玩家每被多击倒一次，成绩指标将平均下降2.08%；玩家驾驶距离每增加100m，成绩指标将平均上升4.36%，行走距离每增加100m，成绩指标将平均上升1.24%；每多造成100点伤害，成绩指标将平均上升0.64%；每多击杀一位敌人，成绩指标将平均上升0.96%；每多存活100s，成绩指标将平均上升4.2%.一系列由模型得出的结论和直觉相符合。

3.6.2Logit回归

       根据”team_placement”（玩家所在队伍最终排名）计算0-1变量“chicken”，（排名为1则chicken取1，表示吃鸡成功，否则取0）。但data1中chicken为1的样本仅占总样本量的2.86%，属于类别不平衡问题，故对chicken取0的样本进行随机抽样，使得正反例数目相等。在此数据处理基础上进行Logit回归，回归结果如下。

     

                     

       显示”player_dbno”（玩家被击倒次数）变量未通过t-test显著性检验，在无明显多重共线性的情况下，剔除该变量拟合新模型，结果如下。

 

模型通过显著性检验且无明显多重共线性问题，方程如（2）式所示。

表4 方程（2）所涉及变量

从方程（2）可看出，击杀敌人数量和玩家存活时间和是否吃鸡呈正相关，每多击杀一名敌人，吃鸡的优势比将平均乘以exp(0.33)=1.39，每多存活100s，吃鸡的优势比将平均乘以exp(0.523)=1.69，这和方程（1）基本保持一致。

但其余变量

“player_dist_ride”、“player_dist_walk”和“player_dmg”对能否吃鸡的影响方向和方程（1）相反。原因可能是由于吃鸡的方式有很多种，比如打法激进、行进距离远的玩家和打法保守、移动范围小的玩家都有可能吃鸡，移动距离和最终是否吃鸡便不一定呈正相关，但总的来说和最终排名是呈正相关的。换言之，吃鸡中的运气成分更高，数据波动更大，而反映排名高低的数据则更为稳健和符合我们的直觉。

04▶

参考资料

[1] 《大吉大利，今晚如何Python解锁“吃鸡”的正确姿势》

[2] 维基百科：PlayerUnknown'sBattlegrounds

https://en.wikipedia.org/wiki/PlayerUnknown%27s_Battlegrounds

[3]《PUBG<绝地求生>Xbox One版本上市两天销量突破100万套》

http://www.shuangzan.com/NewsInfo/NewsDetail/17387

 

05▶

代码附录

https://github.com/qcneverrepeat/pubg

写在最后

    本文是对《大吉大利，今晚如何用Python解锁“吃鸡”正确姿势》（作者：胡萝卜酱，个人公众号：经管人学数据分析）的模仿，尤其是热力图和生存分析的部分有诸多借鉴。

注：以上部分热力图为Python所作

公众号后台回复关键字即可学习

回复 爬虫             爬虫三大案例实战  
回复 Python        1小时破冰入门

回复 数据挖掘      R语言入门及数据挖掘
回复 人工智能      三个月入门人工智能
回复 数据分析师   数据分析师成长之路 
回复 机器学习      机器学习的商业应用
回复 数据科学      数据科学实战
回复 常用算法      常用数据挖掘算法

爱我请给我好看!