Pytorch【60天修炼计划】之第一阶段——入门:Kaggle实战-房价预测
Kaggle
kaggle是一个著名的供机器学习爱好者交流的平台。网页为https://www.kaggle.com 。
今天为入门阶段的最后一天,我们对kaggle中的房价预测进行实操练习。
项目结构图如下:
按照之前转载知乎大佬的pytorch项目结构进行布置,最终结果如下:
data /
首先从kaggle中将数据集下载下来,即将train.csv和test.csv下载下来,并放到data/dataFile/下
从数据集文件可以发现:
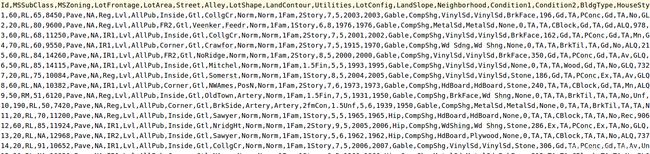
数据集包括每栋房子的特征,有连续值也有离散值,甚至还有缺失值na,所以我们需要将这些数据进行预处理。
因为csv并不能进行数据的操作,所以接下来我们进行数据集的读取:通过pandas读取csv文件。
import pandas as pd
# 1460 × 81 其中最后一列为价格标签
train_data = pd.read_csv('./data/dataFile/train.csv')
# 1459 × 80
test_data = pd.read_csv('./data/dataFile/test.csv')
读取完数据,我们需要进行数据的预处理。
- 将所有训练数据和测试和数据的特征连接
concat起来。 - 对连续数值的特征进行标准化
- 标准化后用0代替缺失值na
- 对离散数值的特征转成指示特征
- 将数据转化为tensor类型
代码依次为:
# 将所有训练数据及测试数据的79个特征按照样本连接
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))
# 对连续数值的特征做标准化
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply(lambda x: (x - x.mean()) / (x.std()))
# 标准化后用0代替缺失值nan
all_features = all_features.fillna(0)
# 对离散数值转成指示特征
# dummy_na = True将缺失值也当作合法的特征值并为其创建指示特征
all_features = pd.get_dummies(all_features, dummy_na=True)
# 再将数据转化为numpy格式的数据,并转为tensor
n_train = train_data.shape[0]
train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float)
test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float)
train_labels = torch.tensor(train_data.SalePrice.values,dtype=torch.float).view(-1, 1)
model /
模型就很简单了,一个Logistics回归就需要一个linear即可。
代码如下:
class Linear(nn.Module):
def __init__(self, feature_num):
super(Linear, self).__init__()
self.linear = nn.Linear(feature_num, 1)
def forward(self, x):
return self.linear(x)
训练模型
取出网络,并定义loss为平方损失函数
def get_net(feature_num):
net = Linear(feature_num)
return net
loss = nn.MSELoss()
再定义比赛用评价模型的对数均方根误差。给定预测值 y 1 ^ , . . . , y n ^ \hat{y_1},...,\hat{y_n} y1^,...,yn^ 和对应的真实标签 y 1 , . . . , y n y_1, ..., y_n y1,...,yn ,它的定义为
1 n ∑ i = 1 n ( l o g ( y i ) − l o g ( y i ^ ) ) 2 \sqrt{\frac{1}{n}\sum_{i=1}^n(log(y_i) - log(\hat{y_i}))^2} n1i=1∑n(log(yi)−log(yi^))2
代码如下:
# 求对数均方根误差
def log_rmse(net, features, labels):
with torch.no_grad():
clipped_preds = torch.max(net(features), torch.tensor(1.0))
rmse = torch.sqrt(2 * loss(clipped_preds.log(), labels.log()).mean())
return rmse.item()
然后进行训练:
def train(net, train_features, train_labels, test_features, test_labels,
num_epochs, learning_rate, weight_decay, batch_size):
train_ls, test_ls = [], []
# 将数据集特征和标签结合起来
dataset = torch.utils.data.TensorDataset(train_features, train_labels)
# 训练集迭代器
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle = True)
# 定义优化器Adam
optimizer = torch.optim.Adam(params=net.parameters(), lr = learning_rate, weight_decay=weight_decay)
net = net.float()
# 进行迭代训练
for epoch in range(num_epochs):
for X, y in train_iter:
l = loss(net(X.float()), y.float())
optimizer.zero_grad()
l.backward()
optimizer.step()
train_ls.append(log_rmse(net, train_features, train_labels))
if test_labels is not None:
test_ls.append(log_rmse(net, test_features, test_labels))
return train_ls, test_ls
K折交叉验证
因为数据集只有训练集和测试集,那么为了得到验证集来选择模型并调节超参数。
所以我们实现一个函数返回第 i i i 折交叉验证时所需要的训练和验证数据
# k折交叉验证,返回第i折交叉验证时所需要的训练和验证数据
def get_k_fold_data(k, i, X, y):
assert k > 1
fold_size = X.shape[0] // k # 返回整数
X_train, y_train = None, None
for j in range(k):
idx = slice(j * fold_size, (j + 1) * fold_size)
X_part, y_part = X[idx, :], y[idx]
if j == i:
X_valid, y_valid = X_part, y_part
elif X_train is None:
X_train, y_train = X_part, y_part
else:
X_train = torch.cat((X_train, X_part), dim = 0)
y_train = torch.cat((y_train, y_part), dim = 0)
return X_train, y_train, X_valid, y_valid
在 K K K 折交叉验证中我们训练 次并返回训练和验证的平均误差。
def k_fold(k, X_train, y_train, num_epochs, learning_rate, weight_decay, batch_size):
train_l_sum, valid_l_sum = 0, 0
for i in range(k):
data = get_k_fold_data(k, i, X_train, y_train)
net = get_net(X_train.shape[1])
train_ls, valid_ls = train(net, *data, num_epochs, learning_rate, weight_decay, batch_size)
train_l_sum += train_ls[-1]
valid_l_sum += valid_ls[-1]
if i == 0:
semilogy(range(1, num_epochs + 1), train_ls,'epochs', 'rmse',range(1, num_epochs + 1), valid_ls,['train', 'valid'])
print('fold %d, train rmse %f, valid rmse %f' % (i, train_ls[-1], valid_ls[-1]))
return train_l_sum / k, valid_l_sum / k
模型的选择。
我们使⽤⼀组未经调优的超参数并计算交叉验证误差。可以改动这些超参数来尽可能减⼩平均测试误
差。
train_data, test_data, train_features, test_features ,train_lables= loadData()
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_lables, num_epochs, lr, weight_decay, batch_size)
print('%d-fold validation: avg train rmse %f, avg valid rmse %f' %(k, train_l, valid_l))
预测
def train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size):
net = get_net(train_features.shape[1])
train_ls, _ = train(net, train_features, train_labels, None, None,
num_epochs, lr, weight_decay, batch_size)
semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse')
print('train rmse %f' % train_ls[-1])
preds = net(test_features).detach().numpy()
test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis = 1)
submission.to_csv('./data/dataFile/submission.csv', index = False)