DBN深度置信网络的实现
“`
深度置信网络(DBN)是由一系列的玻尔兹曼机(RBM)进行叠加组成的。
代码实现DBN的过程,请参考matlab的深度学习工具箱:DeepLearnToolbox 。
而关于深度置信网络的原理部分,请参考大神 peghoty的博客:http://blog.csdn.net/itplus/article/details/19168937。
那么接下来就是自己利用deeplearntoolbox来编写自己的深度置信网络(DBN)了。
DBN函数,包含功能:初始化DBN参数,并进行训练DBN网络,之后将DBN扩展为NN,并对NN进行了相应的初始化,训练以及测试
-
function
DBN(train_x,train_y,test_x,test_y)
-
%单纯的
DBN只是一个
NN网络,它返回的是一个训练好的网络,而不是对测试样本的一个评估
-
%所以,在这个程序中,我们是没有看到输出的结果的
-
%要进行预测,必须要有逻辑回归或者softmax回归才行,因为,这样才能够对测试样本进行评估
-
%初始化参数,层数
-
x = double(train_x)/
255;
-
opts.numepochs =
1;%迭代次数
-
opts.batchsize =
100;%批次处理的大小
-
opts.momentum =
0;%动量(调整梯度)
-
opts.learn_r =
1;%学习率
-
n = size(x,
2);%输入的节点数
-
dbn.layers = [
100
100];%隐层的层数以及节点数
-
dbn.layers = [n,dbn.layers];%输入层+隐层
-
-
%对每层的权重和偏置进行初始化
-
for u =
1:numel(dbn.layers)-
1 %u表示隐层层数
-
dbn.rbm{u}.learn_r = opts.learn_r;
-
dbn.rbm{u}.momentum = opts.momentum;
-
-
dbn.rbm{u}.
W = zeros(dbn.layers(u+
1),dbn.layers(u));%
784*
100的权重矩阵
-
dbn.rbm{u}.vW = zeros(dbn.layers(u+
1),dbn.layers(u));%更新参数用
-
-
dbn.rbm{u}.b = zeros(dbn.layers(u),
1);%b为可见层的偏置
-
dbn.rbm{u}.vb = zeros(dbn.layers(u),
1);
-
-
dbn.rbm{u}.
c = zeros(dbn.layers(u +
1),
1);%
c为隐层的偏置
-
dbn.rbm{u}.vc = zeros(dbn.layers(u +
1),
1);
-
end
-
%初始化参数完毕
-
-
%训练
-
u = numel(dbn.rbm);%隐层的玻尔兹曼机数
-
dbn.rbm{
1} = rbmtrain1(dbn.rbm{
1},x,opts);%训练第一层rbm
-
-
for i =
2:u
-
P = repmat(dbn.rbm{i -
1}.
c’, size(x,
1),
1) + x * dbn.rbm{i -
1}.
W’;
-
x =
1./(
1+exp(-
P));
-
dbn.rbm{i} = rbmtrain1(dbn.rbm{i},x,opts);
-
end
-
figure; visualize(dbn.rbm{
1}.
W’); %
Visualize the
RBM weights
-
-
%训练完毕,并打印特征图
-
-
%展开为nn,利用
BP算法进行参数微调
-
outputsize =
10; %
MNIS数据库,所以最后一层输出只能有
10个
-
nn.layers = [dbn.layers,outputsize];%nn是
DBN展开的,不过还需要其他的一些参数.nn的size表示层数
-
nn.n = numel(nn.layers);
-
nn.activation_function = ‘tanh_opt’; % 激活函数
-
nn.learningRate =
2; % 学习速率
-
nn.momentum =
0.5; % 动量,与梯度有关
-
nn.scaling_learningRate =
1; %
Scaling factor
for the learning rate (each epoch)
-
nn.weightPenaltyL2 =
0; %
L2 regularization
-
nn.nonSparsityPenalty =
0; %
Non sparsity penalty
-
nn.sparsityTarget =
0.05; %
Sparsity target
-
nn.inputZeroMaskedFraction =
0; %
Used
for
Denoising
AutoEncoders
-
nn.testing =
0; %
Internal variable. nntest sets this to one.
-
nn.output = ‘sigm’; % 输出是线性、softmax、还是sigm?
-
nn.dropoutFraction =
0; %
Dropout level (http:
//www.cs.toronto.edu/~hinton/absps/dropout.pdf)
-
for i =
2:nn.n
-
nn.
W{i -
1} = (rand(nn.layers(i),nn.layers(i-
1)+
1)-
0.5)*
2*
4*sqrt(
6/(nn.layers(i)+nn.layers(i-
1)));
-
%注意,这儿必须进行权重初始化,因为输出层的权重并没有设置,而且在后面会
W会被
DBN训练好的权重覆盖
-
nn.vW{i -
1} = zeros(size(nn.
W{i -
1}));
-
nn.p{i} = zeros(
1,nn.layers(i));%该参数是用来进行稀疏的
-
end
-
-
for i =
1: numel(dbn.rbm)%利用了
DBN调整的权重
-
nn.
W{i} = [dbn.rbm{i}.
c dbn.rbm{i}.
W];%注意,我们已经将偏置和权重一块放入nn.
W{i}中
-
end
-
nn.activation_function = ‘sigm’;
-
-
%到此,
DBN扩展为
NN并且进行了初始化
-
-
%接着进行训练
-
-
x1 = double(train_x) /
255;
-
test_x = double(test_x) /
255;
-
y1 = double(train_y);
-
test_y = double(test_y);
-
-
nn = nntrain1(nn, x1, y1, opts);
-
%训练完毕
-
%进行样本测试
-
labels = nnpredict1(nn,test_x);
-
[dummy,expected] =
max(test_y,[],
2);
-
bad =
find(labels~= expected);
-
er = numel(bad) / size(test_x,
1);
-
-
assert(er <
0.10, ‘
Too big error’);
-
end
rbmtrain1函数:这个过程就是对DBN进行训练的过程,要注意的是,对DBN的训练仅仅只是让DBN进行特征学习,而这个过程DBN是无法进行决策,判断的,其训练过程中参数的更新主要依赖样本的变化,返回的是一个进过训练的网络(这个网络还没有输出)。
-
function rbm = rbmtrain1(rbm,x,opts)
-
assert(isfloat(x),
'x must be a float');
-
assert(all(x(:)>=
0) && all(x(:)<=
1),
'all data in x must be in [0,1]');
-
-
m =size(x,
1); %返回x的行数,即样本数量
-
numbatches = m/opts.batchsize;%每 batchsize个样本作为一组
-
-
assert(
rem(numbatches,
1)==
0,
'numbatches not int');
-
-
for i =
1:opts.numepochs
-
seq = randperm(m);%seq 是
1-m的随机数序列
-
err =
0 ;%误差
-
for l =
1:numbatches
-
batch = x(seq((l
-1)*opts.batchsize +
1:l*opts.batchsize),:);%取x的
100个样本
-
%下面的过程是进行GIBBS采样,也算是CD-k算法的实现
-
v1 = batch;%v1表示可见层的初始化,共
100个样本
-
P1 = repmat(rbm.c
', opts.batchsize, 1) + v1 * rbm.W';
-
h1 =
double(
1./(
1+exp(-P1)) > rand(size(P1)));
-
P2 = repmat(rbm.b
', opts.batchsize, 1) + h1 * rbm.W;
-
v2 =
double(
1./(
1+exp(-P2)) > rand(size(P2)));
-
P3 = repmat(rbm.c
', opts.batchsize, 1) + v2 * rbm.W';
-
h2 =
1./(
1+exp(-P3));
-
%参数的更新
-
c1 = h1
' * v1;
-
c2 = h2
' * v2;
-
-
rbm.vW = rbm.momentum * rbm.vW + rbm.learn_r * (c1 - c2) / opts.batchsize;
-
rbm.vb = rbm.momentum * rbm.vb + rbm.learn_r * sum(v1 - v2)
' / opts.batchsize;
-
rbm.vc = rbm.momentum * rbm.vc + rbm.learn_r * sum(h1 - h2)
' / opts.batchsize;
-
-
rbm.W = rbm.W + rbm.vW;
-
rbm.b = rbm.b + rbm.vb;
-
rbm.c = rbm.c + rbm.vc;
-
-
err = err + sum(sum((v1 - v2) .^
2)) / opts.batchsize;
-
end
-
-
disp([
'epoch ' num2str(i) '/' num2str(opts.numepochs) '. Average reconstruction error is: ' num2str(err / numbatches)]);
-
-
end
-
nntrain1函数:主要包含了前馈传播,后向传播(BP算法实现),参数更新,以及性能评估等过程
-
function nn = nntrain1( nn, x, y, opts,val_x,val_y)
-
assert
(nargin == 4 || nargin == 6,'number of input arguments must be 4 or 6')
;
-
-
loss.train.e = [];%%保存的是对训练数据进行前向传递,根据得到的网络输出值计算损失,并保存
-
%在nneval那里有改变,loss.train.e(
end +
1) = nn.L;
-
-
loss.train.e_frac = []; %保存的是:对分类问题,用训练数据对网络进行测试,
-
%首先用网络预测得到预测分类,用预测分类与实际标签进行对比,保存错分样本的个数
-
-
loss.val.e = [];%有关验证集
-
-
loss.val.e_frac = [];
-
-
opts.validation =
0;
-
if nargin ==
6%nargin表示参数个数,
4个或者
6个(val_x,val_y是可选项)
-
opts.validation =
1;
-
end
-
-
fhandle = [];
-
if isfield(opts,
'plot') && opts.plot ==
1
-
fhandle = figure();
-
end
-
-
m = size(x,
1);
-
-
batchsize = opts.batchsize;%批次处理的数目 为
100
-
numepochs = opts.numepochs;%迭代次数 为
1
-
-
numbatches = m/batchsize;%批次处理的次数
-
-
assert(rem(numbatches,
1) ==
0,
'numbatches must be int');
-
-
L = zeros(numepochs * numbatches,
1);%L用来存储每个训练小批量的平方误差
-
n =
1;%n作为L的索引
-
-
for i=
1:numepochs
-
tic;% tic用来保存当前时间,而后使用toc来记录程序完成时间,
-
%差值为二者之间程序运行的时间,单位:s
-
seq = randperm(m);
-
%每次选择一个batch进行训练,每次训练都讲更新网络参数和误差,由nnff,nnbp,nnapplygrads实现:
-
for l =
1 : numbatches
-
batch_x = x(seq((l-
1) * batchsize +
1 : l * batchsize),:);
-
%每
100个为一组进行处理
-
%添加噪声
-
if(nn.inputZeroMaskedFraction ~=
0)%nn参数设置中有,设置为
0
-
batch_x = batch_x.*(rand(size(batch_x)) > nn.inputZeroMaskedFraction);
-
end
-
batch_y = y(seq((l-
1) * batchsize +
1 : l * batchsize),:);
-
-
nn = nnff1(nn,batch_x,batch_y);%进行前向传播
-
nn = nnbp1(nn);%后向传播
-
nn = nnapplygrads1(nn);%进行梯度下降
-
-
L(n) = nn.L;%记录批次的损失,n作为下标
-
n = n+
1;
-
end
-
t = toc;
-
%用nneval和训练数据,评价网络性能
-
if opts.validation ==
1
-
loss = nneval1(nn, loss, x, y, val_x, val_y);
-
str_perf = sprintf(
'; Full-batch train mse = %f, val mse = %f', loss.train.e(
end), loss.val.e(
end));
-
else
-
%在nneval函数里对网络进行评价,继续用训练数据,并得到错分的样本数和错分率,都存在了loss里
-
loss = nneval1(nn, loss, x, y);
-
str_perf = sprintf(
'; Full-batch train err = %f', loss.train.e(
end));
-
end
-
%下面是画图函数
-
if ishandle(fhandle)
-
nnupdatefigures1(nn, fhandle, loss, opts, i);
-
end
-
-
disp([
'epoch ' num2str(i)
'/' num2str(opts.numepochs)
'. Took ' num2str(t)
' seconds'
'. Mini-batch mean squared error on training set is ' num2str(mean(L((n-numbatches):(n-
1)))) str_perf]);
-
nn.learningRate = nn.learningRate * nn.scaling_learningRate;
-
end
-
end
nnff1函数:进行前馈传播,即就是有输入的数据进行计算隐层节点,输出节点的输出
-
function nn = nnff1( nn,x,y )
-
%前馈传播
-
n
=
nn
.
n
;%网络层数
-
m = size(x,
1);%样本个数:应该为
100
-
-
x = [ones(m,
1) x];%应该是
100*
785数组,第一列全为
1,后
784列为样本值
-
nn.a
{1} = x;%nn.a
{i}表示第i层的输出值,所以a
{n}也就表示输出层的结果
-
-
for i =
2 :n-
1
-
switch nn.activation_function
-
case
'sigm'
-
P = nn.a
{i - 1} * nn.W
{i - 1}
';%注意:这儿已经把偏置计算进去了
-
%因为在前面展开的时候,将偏置放在了nn.W{i} = [dbn.rbm{i}.c dbn.rbm{i}.W];中
-
%并且对训练样本添加了一列,这一列就对应这偏置的计算
-
nn.a{i} = 1./(1+exp(-P));
-
case 'tanh_opt
'
-
P = nn.a{i - 1} * nn.W{i - 1}';
-
nn.a
{i} =
1.7159*tanh(
2/
3.*P);
-
end
-
-
%dropout
-
if(nn.dropoutFraction >
0)
-
if(nn.testing)
-
nn.a
{i} = aa.a
{i}.* (
1 - nn.dropoutFraction);
-
else
-
nn.dropOutMask
{i} = (rand(size(nn.a
{i}))>nn.dropoutFraction);
-
nn.a
{i} = nn.a
{i}.*nn.dropOutMask
{i};
-
end
-
end
-
-
%计算使用稀疏性的指数级激活
-
if(nn.nonSparsityPenalty>
0)
-
nn.p
{i} =
0.99 * nn.p
{i} +
0.01 * mean(nn.a
{i},
1);
-
end
-
nn.a
{i} = [ones(m,
1) nn.a
{i}];
-
end
-
-
switch nn.output
-
case
'sigm'
-
P = nn.a
{n - 1} * nn.W
{n - 1}
';
-
nn.a{n} = 1./(1+exp(-P));
-
case 'linear
'
-
nn.a{n} = nn.a{n-1} * nn.W{n-1}';
-
case
'softmax'
-
nn.a
{n} = nn.a
{n - 1} * nn.W
{n - 1}
';
-
nn.a{n} = exp(bsxfun(@minus, nn.a{n}, max(nn.a{n},[],2)));
-
nn.a{n} = bsxfun(@rdivide, nn.a{n}, sum(nn.a{n}, 2));
-
end
-
-
%损失
-
nn.e= y-nn.a{n};%损失,差值
-
switch nn.output%除m是为了平均误差-也可以认为是单个样本的误差
-
case {'sigm
','linear
'}
-
nn.L = 1/2 * sum(sum(nn.e .^2)) /m;
-
case 'softmax
'
-
nn.L = -sum(sum(y .* log(nn.a{n}))) /m;
-
end
-
end
nnbp1函数:后向传播即就是BP算法的实现:
-
function nn= nnbp1( nn )
-
%进行后向传播算法
-
n = nn.n;
-
sparsityError =
0;
-
switch nn.output%本步骤表示输出层单个节点的差值(-(yi-ai)*f
'(zi)),即就是BP第二步,第一步是前馈传播,计算各节点的输出值
-
case
'sigm'
-
d{n} = -nn.e .*(nn.a{n} .* (
1-nn.a{n}));
-
case {
'softmax','linear'}
-
d{n} = -nn.e;
-
end
-
-
for i = (n
-1):
-1:
2%d_act表示激活函数的导数
-
switch nn.activation_function
-
case
'sigm'
-
d_act = nn.a{i} .*(
1-nn.a{i});
-
case
'tanh-opt'
-
d_act =
1.7159 *
2/
3 * (
1 -
1/(
1.7159)^
2 * nn.a{i}.^
2);
-
end
-
-
if(nn.nonSparsityPenalty>
0)%稀疏时有用
-
pi = repmat(nn.p{i}, size(nn.a{i},
1),
1);
-
sparsityError = [zeros(size(nn.a{i},
1),
1) nn.nonSparsityPenalty * (-nn.sparsityTarget ./ pi + (
1 - nn.sparsityTarget) ./ (
1 - pi))];
-
end
-
-
if i+
1 == n%BP算法的第三步
-
d{i} = (d{i +
1} * nn.W{i} + sparsityError) .* d_act;
-
else
-
d{i} = (d{i +
1}(:,
2:
end) * nn.W{i} + sparsityError) .* d_act;
-
%注意,在这儿第一列是偏置,所以要进行移除
-
end
-
-
if(nn.dropoutFraction>
0)
-
d{i} = d{i} .* [ones(size(d{i},
1),
1) nn.dropOutMask{i}];
-
end
-
end
-
for i =
1 : (n
-1)%由于每层的节点数是不一样的,所以需要用除以size(d{i])来求平均节点误差
-
if i+
1 == n%dW表示的是梯度
-
nn.dW{i} = (d{i +
1}
' * nn.a{i}) / size(d{i + 1}, 1);
-
else
-
nn.dW{i} = (d{i +
1}(:,
2:
end)
' * nn.a{i}) / size(d{i + 1}, 1);
-
end
-
end
-
end
nnapplygras1d函数:在BP算法后,进行参数的更新,该函数和nnbp1在整个DBN过程中可以认为是微调阶段
-
function nn = nnapplygrads1(nn)
-
%更新参数的函数
-
for
i
=1:(nn.n-
1)%的W本身包括偏置和权重
-
if(nn.weightPenaltyL2>
0)%L2处罚用
-
dW = nn.dW
{i} + nn.weightPenaltyL2 * [zeros(size(nn.W
{i},
1),
1) nn.W
{i}(:,
2:
end)];
-
else
-
dW = nn.dW
{i};
-
end
-
-
dW = nn.learningRate * dW;
-
-
if(nn.momentum >
0)
-
nn.vW
{i} = nn.momentum * nn.vW
{i} + dW;
-
dW = nn.vW
{i};
-
end
-
nn.W
{i} = nn.W
{i} - dW;
-
end
-
end
-
-
function [ loss ] = nneval1(nn, loss, x, y, val_x, val_y)
-
%评估网路性能
-
assert
(nargin ==4 || nargin == 6,'Wrong number of argument')
;
-
-
nn.testing =
1;
-
%训练性能
-
nn = nnff1(nn,x,y);
-
loss.train.e(
end+
1) = nn.L;
-
%验证性能
-
if nargin ==
6
-
nn = nnff1(nn,val_x,val_y);
-
loss.val.e(
end+
1) = nn.L;
-
end
-
-
nn.testing =
0;
-
%错分类率
-
if strcmp(nn.output,
'softmax')
-
[er_train, dummy] = nntest(nn, train_x, train_y);
-
loss.train.e_frac(
end+
1) = er_train;
-
-
if nargin ==
6
-
[er_val, dummy] = nntest(nn, val_x, val_y);
-
loss.val.e_frac(
end+
1) = er_val;
-
end
-
end
-
end
-
最后就是进行数据的测试
-
function labels = nnpredict1(nn,x)
-
nn
.
testing
= 1;
-
nn = nnff1(nn, x, zeros(size(x,
1), nn.layers(
end)));
-
nn.testing =
0;
-
-
[dummy, i] = max(nn.a
{end},[],
2);
-
labels = i;
-
-
end
-
到此,整个代码的实现过程结束
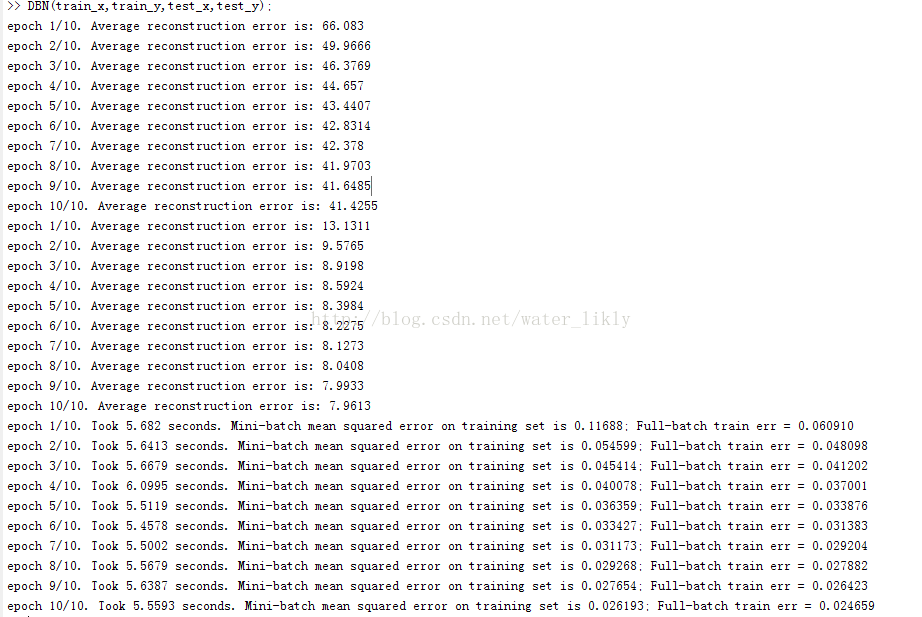
代码运行结果:3层隐层,各100个节点,numepochs=1
2层隐层,各100 节点,numepochs=10:
总结:DBN在运行过程中只是进行特征学习,而无法进行决策,所以在进行DBN训练完成后,需要将DBN扩展为NN,即添加输出层(根据分类结果天天输出层的节点数)。然后,用训练好的DBN的参数初始化NN的参数,进而在进行传统的NN训练,就是进行前馈传播,后向传播等,这样的过程就是完成了DBN的预训练-微调过程。这样之后才可以进行判断,分类等。
以上是我个人在学习DBN过程的一点小心得,若有不足,恳请指正。
“