二叉堆的实现（最大堆）

二叉堆的介绍

二叉堆是完全二元树或者是近似完全二元树，按照数据的排列方式可以分为两种：最大堆和最小堆。
最大堆：父结点的键值总是大于或等于任何一个子节点的键值；最小堆：父结点的键值总是小于或等于任何一个子节点的键值。示意图如下：

二叉堆一般都通过"数组"来实现。数组实现的二叉堆，父节点和子节点的位置存在一定的关系。

1. 索引为i的左孩子的索引是 (2*i+1);
2. 索引为i的左孩子的索引是 (2*i+2);
3. 索引为i的父结点的索引是 floor((i-1)/2);

二叉堆的添加

假设在最大堆[90,80,70,60,40,30,20,10,50]种添加85，需要执行的步骤如下：

如上图所示，当向最大堆中添加数据时：先将数据加入到最大堆的最后，然后尽可能把这个元素往上挪，直到挪不动为止！
将85添加到[90,80,70,60,40,30,20,10,50]中后，最大堆变成了[90,85,70,60,80,30,20,10,50,40]。

二叉堆的删除

假设从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90，需要执行的步骤如下：

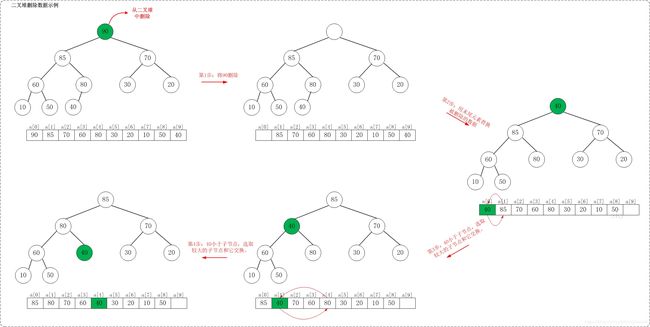
如上图所示，当从最大堆中删除数据时：先删除该数据，然后用最大堆中最后一个的元素插入这个空位；接着，把这个“空位”尽量往下挪，直到剩余的数据变成一个最大堆。
从[90,85,70,60,80,30,20,10,50,40]删除90之后，最大堆变成了[85,80,70,60,40,30,20,10,50]。
注意：考虑从最大堆[90,85,70,60,80,30,20,10,50,40]中删除60，执行的步骤不能单纯的用它的字节点来替换；而必须考虑到"替换后的树仍然要是最大堆"！

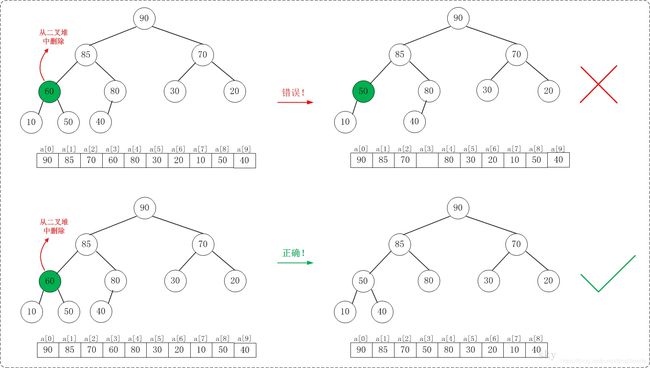
二叉堆的实现

#pragma once
#include 
#include 

using namespace std;

template
struct MaxHeap {
	MaxHeap();
	MaxHeap(int _mCapacity);
	~MaxHeap();
	
	void insert(T &data);					//增加元素
	void remove(T &data);					//删除元素
	void print();							//打印堆
private:
	void filterUp(int start);				//最大堆的向上调整，添加堆元素时使用
	void filterDown(int start, int end);	//最大堆的向下调整，删除堆元素时调用
	int getIndex(T &data);					//获取元素索引
	
private:
	int mCapacity;	//总的容量
	int mSize;		//当前大小
	T * mHeap;		//数据
};

template
MaxHeap::MaxHeap()
{
	new (this)MaxHeap(30);  //使用new (this)重用构造函数
}

template
MaxHeap::MaxHeap(int _mCapacity) : mCapacity(_mCapacity), mSize(0)
{
	mHeap = new T[mCapacity];
}

template
MaxHeap::~MaxHeap()
{
	if (NULL != mHeap)
	{
		delete[] mHeap;
	}
	mCapacity = 0;
	mSize = 0;
}

template
void MaxHeap::filterUp(int start)
{
	int cur = start;
	int par = (cur - 1) / 2;
	T tmp = mHeap[cur];
	while (cur > 0)		//注意此处退出循环条件：cur > 0
	{
		if (mHeap[par] >= tmp)
			break;
		mHeap[cur] = mHeap[par];
		cur = par;
		par = (cur - 1) / 2;
	}
	mHeap[cur] = tmp;
}

template
void MaxHeap::insert(T &data)
{
	if (mSize == mCapacity)
	{
		cout << "insert error, cur heap is full now!" << endl;
		return;
	}
	mHeap[mSize] = data;
	filterUp(mSize);
	mSize++;		//先插入调整后，当前大小再加1
}

template
void MaxHeap::filterDown(int start, int end)
{
	int cur = start;
	int lch = 2 * cur + 1;
	T tmp = mHeap[cur];
	while (lch <= end)
	{
		if (lch < end && mHeap[lch] < mHeap[lch + 1])
			lch++;
		if (tmp >= mHeap[lch])
		{
			break;
		}
		mHeap[cur] = mHeap[lch];
		cur = lch;
		lch = 2 * cur + 1;
	}
	mHeap[cur] = tmp;
}

template
void MaxHeap::remove(T &data)
{
	if (mSize == 0)
	{
		cout << "remove error, cur heap is empty now!" << endl;
		return;
	}
	int index = getIndex(data);
	if (-1 == index)
	{
		cout << "remove error, cur data is not in the heap!" << endl;
		return;
	}

	mHeap[index] = mHeap[--mSize];
	filterDown(index, mSize);		//先减小大小，再向下调整
}

template
int MaxHeap::getIndex(T &data)
{
	int index = 0;
	for (index = 0; index < mSize; index++)
	{
		if (mHeap[index] == data)
			return index;
	}
	return -1;
}

template
void MaxHeap::print()
{
	for (int i = 0; i

测试代码如下：

void maxHeapTest()
	{
		int a[] = { 10, 40, 30, 60, 90, 70, 20, 50, 80 };
		int i, len = (sizeof(a)) / (sizeof(a[0]));
		MaxHeap* tree = new MaxHeap();
	
		cout << "== 依次添加: ";
		for (i = 0; iinsert(a[i]);
		}
	
		cout << "\n== 最 大 堆: ";
		tree->print();
	
		i = 85;
		tree->insert(i);
		cout << "\n== 添加元素: " << i;
		cout << "\n== 最 大 堆: ";
		tree->print();
		
		i = 90;
		tree->remove(i);
		cout << "\n== 删除元素: " << i;
		cout << "\n== 最 大 堆: ";
		tree->print();
		cout << endl;
		delete tree;
	}

原文链接如下：https://www.cnblogs.com/skywang12345/p/3610382.html