RoIPooling与RoIAlign的区别

一、RoIPooling与RoIAlign

1.1、RoIPooling

通过对Faster RCNN的学习我妈了解的RolPooling可以使生成的候选框region proposal映射产生固定大小的feature map

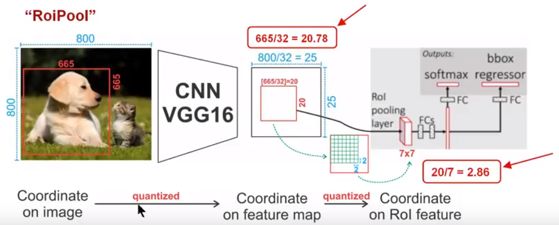
先贴出一张图，接着通过这图解释RoiPooling的工作原理 

针对上图      

1)Conv layers使用的是VGG16，feat_stride=32(即表示，经过网络层后图片缩小为原图的1/32),原图800*800,最后一层特征图feature map大小:25*25      

2)假定原图中有一region proposal，大小为665*665，这样，映射到特征图中的大小：665/32=20.78,即20.78*20.78，如果你看过Caffe的Roi Pooling的C++源码，在计算的时候会进行取整操作，于是，进行所谓的第一次量化，即映射的特征图大小为20*20      

3)假定pooled_w=7,pooled_h=7,即pooling后固定成7*7大小的特征图，所以，将上面在 feature map上映射的20*20的 region proposal划分成49个同等大小的小区域，每个小区域的大小20/7=2.86,即2.86*2.86，此时，进行第二次量化，故小区域大小变成2*2

4)每个2*2的小区域里，取出其中最大的像素值，作为这一个区域的‘代表’，这样，49个小区域就输出49个像素值，组成7*7大小的feature map    

总结，所以，通过上面可以看出，经过两次量化，即将浮点数取整，原本在特征图上映射的20*20大小的region proposal，偏差成大小为14*14的，这样的像素偏差势必会对后层的回归定位产生影响    

所以，产生了替代方案，RoiAlign

 

1.2、RoIAlign

这个是在Mask RCNN中使用以便使生成的候选框region proposal映射产生固定大小的feature map时提出的

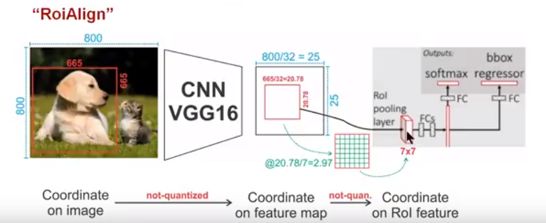
先贴出一张图，接着通过这图解释RoiAlign的工作原理

同样，针对上图，有着类似的映射

1)Conv layers使用的是VGG16，feat_stride=32(即表示，经过网络层后图片缩小为原图的1/32),原图800*800,最后一层特征图feature map大小:25*25

2)假定原图中有一region proposal，大小为665*665，这样，映射到特征图中的大小：665/32=20.78,即20.78*20.78，此时，没有像RoiPooling那样就行取整操作，保留浮点数

3)假定pooled_w=7,pooled_h=7,即pooling后固定成7*7大小的特征图，所以，将在 feature map上映射的20.78*20.78的region proposal 划分成49个同等大小的小区域，每个小区域的大小20.78/7=2.97,即2.97*2.97

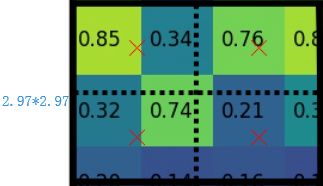
4)假定采样点数为4，即表示，对于每个2.97*2.97的小区域，平分四份，每一份取其中心点位置，而中心点位置的像素，采用双线性插值法（下面介绍）进行计算，这样，就会得到四个点的像素值，如下图

上图中，四个红色叉叉‘×’的像素值是通过双线性插值算法计算得到的

最后，取四个像素值中最大值作为这个小区域(即：2.97*2.97大小的区域)的像素值，如此类推，同样是49个小区域得到49个像素值，组成7*7大小的feature map。

 

上面说到双线性插值法，那么什么是双线性插值法呢？

 

二、双线性插值法（图像插值法）

2.1、为什么要用双线性插值法

在图像的放大和缩小的过程中，需要计算新图像像素点在原图的位置，如果计算的位置不是整数，就需要用到图像的内插，我们需要寻找在原图中最近得像素点赋值给新的像素点，这种方法很简单是最近邻插法，这种方法好理解、简单，但是不实用，会产生是真现象，产生棋盘格效应，更实用的方法就是双线性插值法。

 

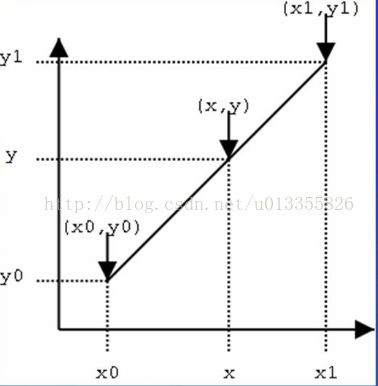
2.2、一维线性插值

我们已经知道（x0，y0）与（x1, y1）的值，并且已知 x 的值，要求 y 的值。根据初中的知识：

我们可以得到:.     

令：

则：

 

2.3、双线性插值法的推导过程

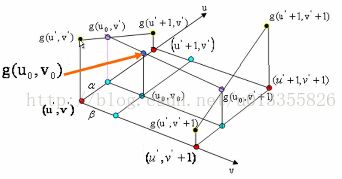
双线性插值是做了二次一维的线性插值，我们用四个最近邻估计给定的灰度。我们新图像的像素点对应输入图像的（u0 , v0）(u0,v0不是整数)，则其必定落在原始图像四个像素点中间。四个像素点分别是（u' , v' ）、（u' , v' +1）、（u'+1 , v' ）、（u' +1, v'+1 ）。如下图1所示：

图一图二

图三图四

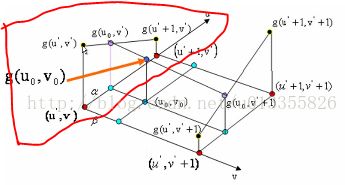
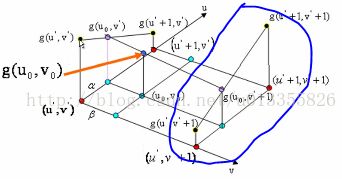
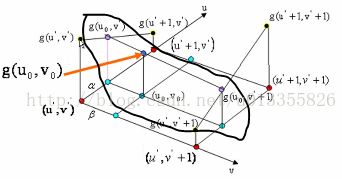
如图2所示：在红色平面内，在红色平面内，只有u' 是变量，v' 是常值，连线 g(u' , v' )、 g(u'+1 , v' )，相当于做一次一维线性插值，求出 g(u0, v' )的值。同理，如图3中，在蓝色的平面内我们可以再做一次一维线性插值，求出g(u0, v' +1)的值。同理如图4，在黑色的平面内，我们可以求出(u0, v0)对应的值g(u0, v0)的值。（双线性插值就是分别在 u、v方向上做线性插值）数学推导过程如下：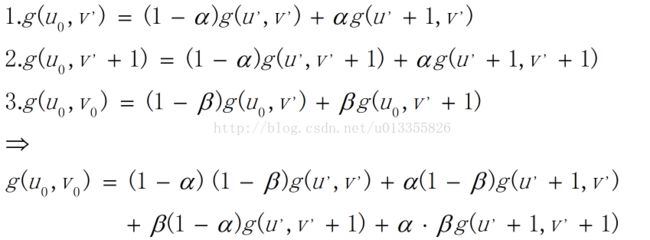

 

三、总结

知道了RoiPooling和RoiAlign实现原理后，在以后的项目中可以根据实际情况进行方案的选择；对于检测图片中大目标物体时，两种方案的差别不大，而如果是图片中有较多小目标物体需要检测，则优先选择RoiAlign，更精准些。

 

本文转自：

https://www.cnblogs.com/wangyong/p/8523814.html

https://blog.csdn.net/u013355826/article/details/56680521