在共享内存实现 Redis（上）

背景

Redis是一个应用广泛的开源NoSql数据库，在腾讯云Redis开发过程中，我们比较深入地对其进行了研究和应用，并和自研的Grocery等数据库系统做了一些对比，总结出了Redis在运营中可能有的一些缺陷：

i. 数据存放在私有内存，升级版本和更新困难，且危险性高（由于内部使用需要给Redis源码内嵌一些自研的库或针对实际需求做一些源码修改，不能直接使用原生Redis）

ii. 内存使用率低，碎片多

iii. 备份、全量同步机制采用fork+rdb的方式，且对内存增长没有做控制，为防止OOM，一般都需要留一半空闲内存

iv. 死机恢复采用全量+增量方式，如果数据量太大并且写量也足够大，有可能占用大量buffer缓冲且出现反复失败的情况

v. 对于所有命令串行处理，有些慢查询如lrange会阻塞其他命令

vi. 存在大包回复时，可能会消耗一大块内存用于存放临时对象，且像上面v.说的一样会卡顿（如dump命令等）

vii. 没有防雪崩之类的海量数据运营机制

通过总结Grocery等自研系统和Redis的优缺点，以及一年多以来的运营情况，公共组件组认为Redis的很多问题和其直接使用进程私有内存管理数据有关，若能像自研数据库一样做到数据逻辑分离，则不但能提高健壮性，对以后的改造也能提供一个安全的基础（解决升级问题，以后再怎么改至少不会危及数据）

于是，我们从实现方式入手，设计了一种综合二者优点的方案：将Redis做成数据逻辑分离，数据存放共享内存，进程只负责存储逻辑，同时解决Redis长命令卡顿和fork引发的相关问题

需求

主要技术需求有两点：

1）大数据要直接存放在共享内存，能直接进行数据结构的存取，操作速度在复杂度上要足够低

2）由于数据和逻辑分离，且有dump的需求，需要针对特定情况，开发对应渐进式存取的需求；同时由于不能使用fork来利用linux的cow机制实现精确快照，也需要其他算法；更进一步地，考虑到将来的发展，可能还需要考虑通用的渐进式存取，并发式存取等，原理类似，这里暂不涉及

内存管理机制

对于共享内存采用Block式的管理，类似Grocery的linktable，将一块共享内存视作固定大小Block的数组，考虑到字节对齐，每个Block大小最好是8的倍数，内存头部可以开辟一块头内存，存放一些元信息，也可以利用开头的若干Block来做元信息储存，下面的设计描述中不区分元信息和数据，仅将其看做以Block为单元的集合

注：由于是在共享内存中管理数据，因此不能用普通的指针来做数据之间的指向和关联，为方便起见，本文档下面描述共享内存数据的指向依然采用“指针”这个词，但是读者应理解为描述共享内存中相对位置的一个整数

共享内存形式和扩缩流程

由于需要实现内存的扩缩，而Sys V的shmXXX系列接口的共享内存对这方面支持并不好，因此选用Posix的共享内存形式，具体地，就是在tmpfs（一般是在/dev/shm目录）下创建文件，然后用mmap的方式映射为共享内存，扩缩流程可采用文件操作：

1 munmap取消对文件的映射

2 打开文件并执行truncate操作，改变文件大小

3 重新mmap到目标大小

如此便可实现共享内存的扩缩容

（实际上通过新建文件/删除文件，还可以把tmpfs当成是共享内存版本的malloc和free来用，但不推荐采用大量小文件的方式，频繁打开关闭文件，或者维持大量文件句柄都是比较耗资源的做法）

Block申请和释放

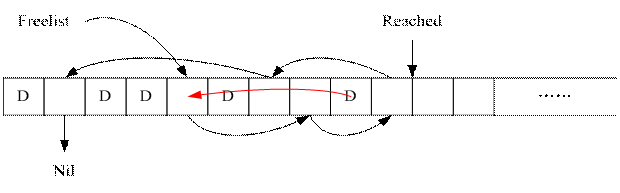
Block的管理方式类似Grocery的linktable，但是做了一些改进，和linktable一样，通过Freelist将已释放的Block用链表（或其他结构）串起来，同时配合一个Reached指针即可实现常数时间的扩容：

如图是一块共享内存空间，其中的格子为固定大小Block，D表示存放着数据，可以看到，Freelist可以将空闲的Block串在一起，但是仅包含Reached指针之前的空闲块，Reached指针表示目前的内存最多用到的位置，其之后的内存块可能是新扩容出来或从上次创建就从来没用到的，全部是空Block

当申请一个Block时采用如下步骤：

1 若Freelist指针不为Nil，则从Freelist头部获取一个空闲Block，同时Freelist指针指向这个Block的next Block

2 否则，说明Freelist里面没有空闲Block，此时如果Reached指针没有达到内存尾部，则说明存在还未使用的新块，将Reached指针指向的Block作为申请到的空闲Block，同时Reached指针后移一个Block

3 否则，说明本内存区已被用满，此时如果允许扩容，则使用前述扩容方法，扩充共享内存大小，然后执行第2步骤，即可申请成功

4 如果无法扩容，则返回无法申请资源的错误

可以看到，引入Reached指针是为了减少扩容的消耗，否则的话，每次扩容需要将新的一批Block顺序加入Freelist，从而是O(N)的时间，引入Reached指针则可将这个过程变成近似O(1)（如上所述，新扩容采用truncate tmpfs文件来做，只是页表修改，实际使用时才映射到共享内存，所以比较快的）

释放一个Block则比较简单，直接加入Freelist即可，若Freelist采用单链表设计，则做一次头插入

缩容

上述过程只涉及到扩容，对于释放Block则是直接加入Freelist，如有必要，我们还需支持一块共享内存数据区的缩容操作，以避免在长时间运行后由于删除操作带来大量浪费内存的空闲Block，缩容操作策略一般可以在数据占有率（即数据Block的数量除以总Block数量）低于一定程度时进行，且应该是渐进式执行

如图，假设此时我们需要缩容这块内存，即采用扩容的反向动作：

1 Reached指针前移

2 通过前述扩缩步骤，缩小内存到目标大小（即truncate这个文件）

主要问题来自于第1步，由于Reached指针前面的Block要么是存放数据，要么是Freelist中，因此需要先将其变成没有任何地方引用的Block，即自由空闲Block，才能前移，具体的做法：

1 所有的块有一个标记，表示自己当前是什么类型（在Freelist中，或者是在某种数据结构中）

2 如果前面的Block空闲，则将其从Freelist中摘除，为了实现快速摘除，Freelist不能是单链表，必须是其他结构，比如双向链表就可以实现O(1)的摘除操作；而如果是一个数据Block，则和具体数据结构有关，需要将这个Block从所属结构摘除，并从FreeList中得到一个新的空闲Block（上图的红色迁移线路，由于这个Block就在Reached指针前面，因此只可能往前迁移），将数据迁移过去并调整好和原数据结构的关系（比如各种指针等），要保证这个过程足够快，数据结构必须支持快速迁移任意节点Block的功能，下述用于实现Redis功能的数据结构都会支持

3 由于是一个个Block缩减，因此是可渐进式进行的，Reached指针的位置达到目标大小后，调用上述的扩缩容流程将整个内存区缩小，即可向操作系统释放内存

可能需要的改进：上图中，最右边数据D的迁移是迁到Freelist指向的第一个空闲Block，但是显然我们将其迁移到更前面的空闲Block（第二个）是更优的一个做法，这样在需要大量迁移数据时可以避免重复劳动，每次都迁到最靠前的Block，要做到这一点，可以将Freelist改进为一个以Block为节点的平衡树，使得所有空闲Block按地址有序排列，这样一来就算在正常的申请释放过程中，也可以保证数据的前向聚集，在缩容时也可以实现更快的速度，只迁移必要的数据Block，而且有些平衡树结构的Freelist当右侧是连续的空闲Block时，可以通过O(lgN)的旋转来批量释放，使得Reached指针一次前向移动若干块，来加速这个过程，所付出的代价是Freelist本身的实现复杂性，以及每次申请释放内存会稍慢一些

基于Block的基本数据结构

在上述共享内存中实现复杂数据结构存储，基本思路就是以Block为节点，将其组织为对应的数据结构，在一般的数据结构中，一个节点只包含一个数据，但是在以Block为节点的数据结构中，一个Block的大小是固定的，如果存放一个较小数据，则浪费空间，而较大数据明显也不可能在一个Block存下，因此，一个Block可能会承载多个数据，或一个数据需要拆分到多个Block存放

我们采用两种基于Block的数据结构：双向链表和平衡树，其节点是Block，数据组织形式设计如下

双向链表

如图，每个矩形为一个Block，若干Block构成一个双向链表，Block内部有一个独立的Head，用于存放类型、前后指针以及其他一些元信息，其中每个Block存放一个或多个数据，且数据在Block内部按序紧凑排列，例如上面的结构就相当于在普通的私有内存中，用一个有9个节点的双向链表管理Elem1到Elem9一样，二者等价

如果一个数据比较大，就算单独占用一个Block节点也无法存放，则需要将其拆为若干份，比如一个超长的字符串，如图（假设这个字符串是直接隶属于db）：

如果一个链表中的数据存在超长字符串，则链表本身可以只记录其指针，将字符串另外存放在Block链表中，如图（假设这个List是直接隶属于db），Elem2由于过大，是单独用Block链表存储，然后List对象中存储其指针，即带方框的Elem2：

这里，所有的实现都是双向链表，不能实现为单向，因为如上面缩容算法所述，需要从任意节点得到其前驱后继，用来做Block的迁移

链表操作

1）查询数据

这里只讨论一般的查询第K个数据，从链表第一个Block开始遍历，Head中存放了本Block的数据数量，因此遍历时可以快速跳数量（如果Head中没有存放，则需要分析本Block数据），当找到第K个数据所在的Block后，用K减去已跳过的数量，则为本Block中的相对位置，分析本Block的紧凑数据，取出Elem即可；针对长字符串的查找第K字节也是类似做法；由于是双向链表，倒数第K个数据也可从尾节点开始往前用同样的算法进行

查找是否存在值为指定值的数据，则需要顺序遍历所有Block的所有数据进行比较，也是通过遍历进行，不再赘述

2）插入数据

通过1）中的查询算法找到要插入的位置，插入数据并重新组织Block数据，若Block因为这次插入而无法存下新组织的数据，则需要一次分裂过程：

如图，上面的一个节点因为插入了Elem6数据而导致数据放不下，于是新引入一个节点（右下方红色），从原节点分出去两个数据，并将新节点插入链表，从而保证了插入过程成功进行

3）删除数据

通过1）中的查询算法找到需要删除的数据，删除掉并重新组织Block数据，若Block由于这次删除被清空，则将Block节点从链表中删除，归还Freelist

Block数据合并

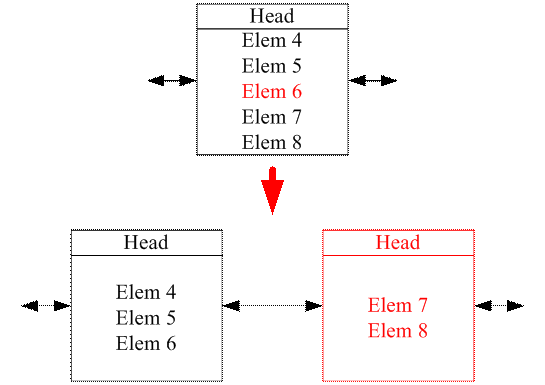
删除数据操作中，如果一个Block没有被清空，则不会归还Freelist，当一个数据结构的数据经历若干插入和删除后，可能形成占用大量Block，但是很多Block中数据并不多的情景，这样会导致内存浪费，所以需要一个操作来合并一些Block，合并操作基本上就是上述分裂节点的逆操作，当一个Block被删除数据，没有被清空的时候，实时查看其前驱和后继，看是否满足合并条件，如果满足，则将两个Block合并，这样可以省下一个Block归还Freelist

如图，从List中删除Elem6后，检测到左边节点由于数据量变小，可以和其后继（右边节点）合并，于是将右边节点的数据（Elem7和8）迁移过来，并将右边节点从List中删除，释放空间

合并过程的一些关键问题：

1）数据合并时机，可以采用每次删除时候都触发，也可以通过后台任务渐进式遍历检查来进行，前者实时性好些

2）合并操作触发的Block数据大小阈值，如果两个Block可以合并，但是合并后比较满，则很可能在下次插入数据时又重新分裂，所以可以定一个阈值，当合并后数据占Block大小仍然小于一定比率，才认为合并操作是有价值的

3）前向和后向合并，两个Block存在前驱和后继的关系，从哪个Block向另一个合并，也是需要考虑的问题，但在链表结构中这个问题不严重

P.S.如果不是删除Elem，而是修改Block中某个Elem数据，使得其数据长度变短，进而整个Block的数据打包后变短，可以和前驱或后继合并的时候，也适用合并操作，当然，如果Elem数据被修改后变长，也可能需要分裂操作

Block数据分摊迁移

上面提到，链表操作在插入的时候，如果由于插入导致被处理的Block的新的数据大小超出Block限制，则需要分裂节点，但是在有些情况下，我们可以不用分裂节点，而是通过将数据向这个Block的前驱或后继移动来实现

如图，和上面插入的例子类似，由于插入了Elem6，导致左边Block的数据超出空间大小，与上面描述的申请新节点分裂Elem7和8的方法不同，这里是将这两个数据迁移至后继节点（假设后继节点空间足够），从而形成了下面的数据布局，不用申请新的Block

分摊迁移的时机可在每次需要分裂时进行判断，尽可能减少Block的分裂，从而提高内存使用率；同上述合并的情况，可以向前驱或后继迁移，具体如何做则看具体需求和算法了

如果是修改Block中的数据，数据长度变长的情况，也适用本操作

平衡树

和双向链表类似，用Block做节点，每个节点内部有多个数据（方便起见这里只描述Key，Value则可以看做Key的一个附属数据）：

如图，每个Key后面的字母可看做是Key的值，可以看到整个平衡树中数据是有序排列，只是每个节点可能存放（连续的）多个Key

同时，平衡树中每个节点还有一个Size属性，用来记录这个节点为根的子树中的Key的数量，通过这个属性可以对树中的数据求其排行，或者求第K个数据，也能方便实现Redis的randomkey之类的操作

平衡树中单个节点的数据存放，以及存放超长字符串的方案同双向链表，不再赘述

平衡树类别的选择

由于此处使用的平衡树是以Block为节点，因此和普通的二叉平衡树没有什么区别，可以任意选用，比如AVL，红黑树，Treap等都可以，具体的选择可能在效率、实现难度以及一些操作细节上有差别，需要看情况而定

为了能支持前面一节设计的内存缩容整理算法，必须能从树中任意一个节点得到和其相关的节点，因此节点必须有一个父指针指向父节点，这样也可以避免相关操作在编程上的递归方式

平衡树的操作

1）根据Key查找数据

类似普通平衡树的查找方式，但是由于每个节点可能有多个数据，而且我们希望在查找失败时并不仅仅告知失败，能同时告知这个Key需要被插入的位置，以便于接下来的操作

因此在做某个节点数据和待查询数据比对时，采用限定范围的方式，范围采用[a,b)的左闭右开空间来表示，其中a和b都是Block，表示Key可能在这两个Block所表示的区间中，显然a应该是b的前驱（直接或间接）

一开始查找时，将区间设置为[begin,end)，begin和end是两个特殊值，类似数学中的正负无穷，表示到树的开头Block和虚拟的结束Block（即最后一个Block之后的一个假想的节点），从树根开始查找：

a）若Key小于当前节点的第一个数据，则区间中的b更新为本节点，之后在左子树递归查找

b）若Key大于当前节点的第一个数据，则区间中的a更新为本节点，之后在右子树递归查找

c）若Key等于当前节点的第一个数据，则立即返回查找成功，以及本节点

d）步骤a和b中，若被递归的子树为空，则判断当前区间，在区间内部的Block的所有数据中依次找Key（此时区间中的Block数量最多为1），若找到则按c步骤进行返回，否则返回查找失败，以及可以Key可以插入的Block节点

举例说明：

如图，假设我们要在这个平衡树中查找Key H，步骤：

A）初始化区间为[begin,end)

B）和根节点NodeD的第一个数据Key M比较，由于H

C）在NodeD的左子树查找，和左子树的根节点NodeB的第一个数据Key G比较，由于H>G，更新区间为[NodeB, NodeD)

D）在NodeB的右子树查找，和右子树根节点NodeC第一个数据Key J比较，由于H

E）在NodeC的左子树查找，由于左子树为空，则区间结果就是[NodeB,NodeC)，这个区间仅包含NodeB一个节点，在这个Block中顺序查找Key H，找到后返回；若Key H并不存在于上面这棵树，则E步骤返回NodeB，表示Key H可以插入到NodeB中

2）根据排名查找数据

由于每个节点的Size属性保存了当前节点为根的子树的数据数量，根据Size就可以实现O(lgN)的查找第K个Key的算法，从根节点开始比较

定义：简单起见，对于每个处理到的节点，下面用NodeSize表示当前节点的Size，左右子树的Size分别是LeftSize和RightSize，若某个子树为空，则Size为0

a）判断K的合法性，假设名次从1开始，则范围是1<=K<=NodeSize，若不合法则根据具体情况返回相应的结果

b）若K<=LeftSize，则在左子树查找第K个数据

c）若K>NodeSize-RightSize，即K比左子树和当前节点的数量总和还要大，则在右子树查找第K-(NodeSize-RightSize)个数据

d）若b和c步骤条件都不符合，则说明第K个数据就在当前节点，遍历当前Block找到第K-LeftSize个数据即可

由于a步骤中已经判断了合法性，因此一定能找到一个数据并返回（除非数据已损坏，Size字段出错）

举例说明：

如图，假设我们要查找树中第6个数据，则流程如下：

A）根据上述步骤的a，根节点Size为10，1<=6<=10，因此输入合法，从根NodeD开始处理

B）NodeD的左子树NodeB.Size是6，根据上述步骤的b，问题转化为NodeB为根的子树查找第6个数据

C）NodeB的左子树NodeA.Size是2，右子树NodeC.Size为2，根据上述步骤的c，继续在右子树NodeC中查找第6-(6-2)=2个数据

D）NodeC没有子树，因此左右子树Size均为0，根据上述步骤的d，数据就在NodeC这个Block，顺序查找到第2个数据，返回Key K，结束

3）插入数据

通过1）中的查找算法找到数据可以插入的Block（假设数据不存在），之后遍历解析出Block内部数据，将需要插入的数据和原Block数据合并并保证按Key有序，再写回Block，如新数据过大，则按照上述双向链表中插入后分裂节点的算法，新申请Block节点，分裂原Block数据并将新Block插入至原Block的后继位置

插入数据后，需要调整插入Block到向上树根的路径的所有节点的Size

Block的分裂过程也适用上述链表的数据分摊迁移算法，不再赘述

4）删除数据

通过1）中的查找算法找到数据所在Block，然后从Block中删掉此数据即可，若Block因为这个删除操作变空，则调用节点删除流程将其从树中摘除并释放到Freelist

删除数据后，也需要调整插入Block到向上树根的路径的所有节点的Size

和链表一样，删除操作也适用合并Block的算法，不再赘述

从平衡树删除一个数据的时间复杂度是O(lgN)，而连续删除M个数据则是O(MlgN)，但是，如果需求是删除平衡树中一段连续数据（比如Redis的zset的zremrangebyXX），则可以通过O(lgN)的旋转，将这段数据旋转为一棵独立子树，然后将其从原树摘除，再用O(M)时间来释放空间，整体操作复杂度O(M+lgN)，不过只有少数平衡树比如Treap支持这样做，可以作为一个优化点（Redis的跳表也是支持这样搞的）

5）节点插入删除 & 平衡树旋转调整 & 查找最大/最小值 & 查找节点前驱/后继

这几种操作与普通的二叉平衡树没有什么区别，针对节点（Block）进行，唯一的区别可能在于旋转过程中的Size调整有些差别，本设计不再赘述

Redis数据结构&数据存取

有了上述基于Block的数据结构设计，对于Redis的各种数据结构就可以比较方便地实现了，需要注意的有几点：

1）长String的实现，上面的例子是用链表，而Redis的String还需要实现range和bitmap的相关功能，所以用平衡树可能更好一点

2）长String的Block中是一个字符串片段，Size域表示的是字节数

3）为省空间，短String可以用各种压缩存储的方式，比如像Redis对于整数做特殊处理

4）Db、Hash、Set和ZSet都可以用平衡树，但各自有一些区别：

i. Hash是普通的KV映射，Set没有Value域，ZSet的Value域是一个double类型的Score

ii. 每个ZSet需要两棵树，第二棵是Score映射Key，按Score的double值排序，Score一致的时候按Key的字母序

iii. Db的实现特殊一点，每个Value不仅对应一个Object，还需要存储一些元数据，比如创建时间，lru信息等