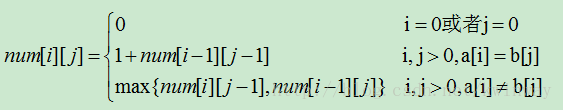最长公共子序列问题和动态规划

最长子序列问题

子序列定义

可以注意到,子序列不要求所选的字母连续,只要求是按原次序组成就好
这是和子串的一个区别

##最长公共子序列定义
最长公共子序列(L ongest C ommon S equence)
简称为LCS,下同

直观明了,就是两个序列的共有的子序列中最长的一个,
此图里就是 DATA这一个单词
#解法
##1. 暴力法
首先我们想到的便是把两个序列的所有可能的子序列枚举出来,一一进行比较.

所有一个序列的子序列的组合有 **$2^n$**种可能,而且需要m次比较.

所以时间复杂度是O($m\ast 2^n$),空间复杂度是O(2^n);

显然出现了 指数形式的复杂度,这是在时间和空间上无法接受的.
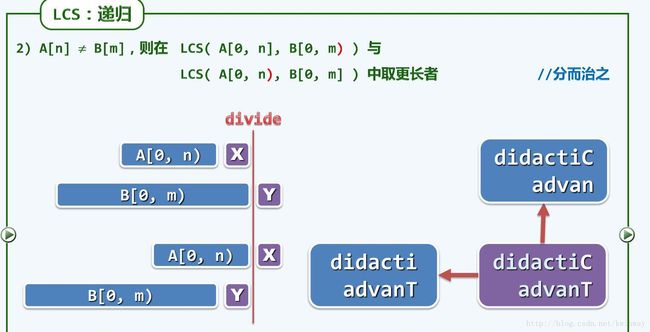
##2 递归
对于序列A[0,N] 和A[0,M];
他们的最长自序列LCS(A,B)有三种情况

①. 最后一个字母相等,直接将其剔除

②.末子符不等

这有点不好理解,其实在开始递归时 ,程序并不知道谁能取得更大的字串,

所以将分别对应的两种情况都进行递归直到递归出口,(相当于将每种情况都走完)

之后把所有的情况每次都层层返回,

每次返回都进行一次比较,总是取最大的返回值,这样就得到了更长者

③.递归出口

当序列为空的时候,返回0;

总结下来就是如下公式

根据这个公式很容易得出递归版的代码

#define _CRT_SECURE_NO_WARNINGS 1
#include
#include

char a[30], b[30];
int a_len, lenb;
int LCS(int, int);

int main()
{
	strcpy(a, "ABCBDAB");
	strcpy(b, "BDCABA");
	a_len = strlen(a);
	b_len = strlen(b);
	printf("%d\n", LCS(a_len - 1, b_len - 1));//从末尾开始递归
	getchar();
	return 0;
}

int LCS(int i, int j)
{ 
	if (i <0|| j <0)
		return 0;
	if (a[i] == b[j])
		return 1 + LCS(i -1, j-1);
	else
		return LCS(i -1, j)>LCS(i, j - 1) ? LCS(i - 1, j) : LCS(i, j - 1);
}

考虑算法的复杂度
时间复杂度在最好的情况下
例如,两个序列相等,只需要O(n)线性时间内完成,
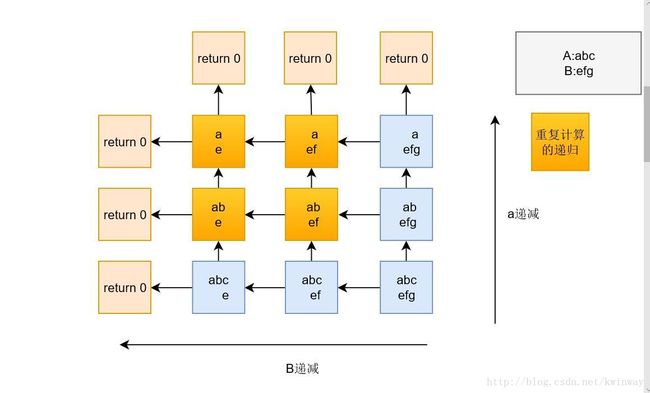
但若在最坏的情况下,
每进行一次递归,就会引发新的两个问题,
而新的两个问题又会引发各自新的问题,
重点是在各自的问题中会出现大量重复的问题.导致时间复杂度激增.
为O($ 2^n$)
最坏情况下的递归例子如图

动态规划求解

我们提到,用递归解决此问题最大一个问题就是:
当不是最优解时总会出现重复计算的递归
为了解决这个问题,首先想到可以用一张表存入已计算的数据,
在计算之前先查表需要计算的数据是否存在,若不存在则再计算.
这是一种以空间复杂度换取时间复杂度的做法.
出现重复递归的本质是在每一次递归的不确定性,当末序列不相同时,是向右走还是向上走是未知的.如何具体确定路径呢?
我们可以从头开始画一张表

每个方块代表问题的解
从左往右,从上到下一次将这张表填满.规则如下

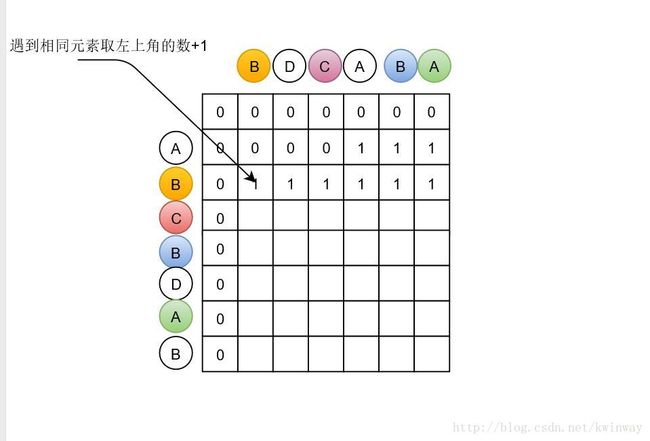
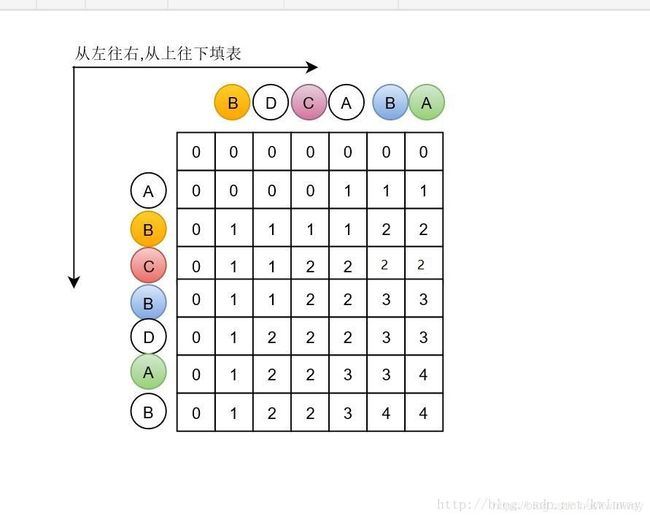
当然会出现多解和歧义解的情况,但不在本问题讨论之内.

这张表就表示了所有可能出现的情况,从左上角或者右下角开始进行推到,很容易得到正确的结果.而且不会重复计算
以从右下角为例

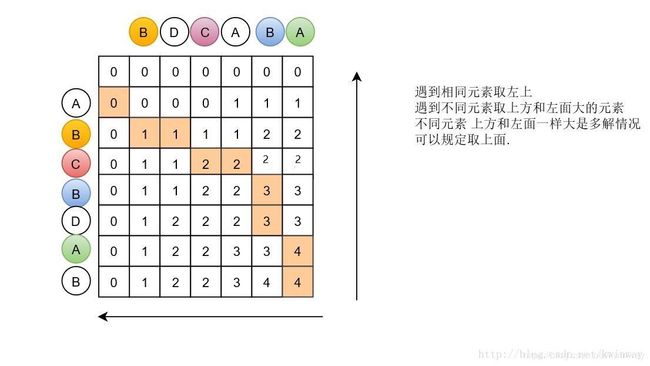
总能取出一个最长子序列BCBA
下面是代码

#define _CRT_SECURE_NO_WARNINGS 1

#include
#include

char a[500], b[500];
char num[501][501]; ///记录中间结果的数组
char flag[501][501];    ///标记数组，用于标识下标的走向，构造出公共子序列
void LCS(); ///动态规划求解
void getLCS();    ///采用倒推方式求最长公共子序列

int main()
{
	int i;
	strcpy(a, "CDEFG");
	strcpy(b, "BDCABA");
	memset(num, 0, sizeof(num));
	memset(flag, 0, sizeof(flag));
	LCS();
	printf("%d\n", num[strlen(a)][strlen(b)]);
	getLCS();
	getchar();
	return 0;
}

void LCS()
{
	int i, j;
	for (i = 1; i <= strlen(a); i++)
	{
		for (j = 1; j <= strlen(b); j++)
		{
			if (a[i - 1] == b[j - 1])   ///注意这里的下标是i-1与j-1
			{
				num[i][j] = num[i - 1][j - 1] + 1;
				flag[i][j] = 1;  ///对角线
			}
			else if (num[i][j - 1]>num[i - 1][j])
			{
				num[i][j] = num[i][j - 1];
				flag[i][j] = 2;  ///向左
			}
			else
			{
				num[i][j] = num[i - 1][j];
				flag[i][j] = 3;  ///向上 
			}
		}
	}
}

void getLCS()
{

	char res[500];
	int i = strlen(a);
	int j = strlen(b);
	int k = 0;    ///用于保存结果的数组标志位
	while (i>0 && j>0)
	{
		if (flag[i][j] == 1)   ///如果是对角线标记
		{
			res[k] = a[i - 1];
			k++;
			i--;
			j--;
		}
		else if (flag[i][j] == 2)  ///如果是向左标记
			j--;
		else if (flag[i][j] == 3)  ///如果是向上标记
			i--;
	}

	for (i = k - 1; i >= 0; i--)
		printf("%c", res[i]);
}

参考:
1.数据结构MOOC PPT
2.https://www.cnblogs.com/xudong-bupt/archive/2013/03/15/2959039.html