非监督学习（二）VAE（生成二次元人脸）

版权声明：本文为原创文章，未经博主允许不得用于商业用途。

2. VAE

2.1 原理

概述

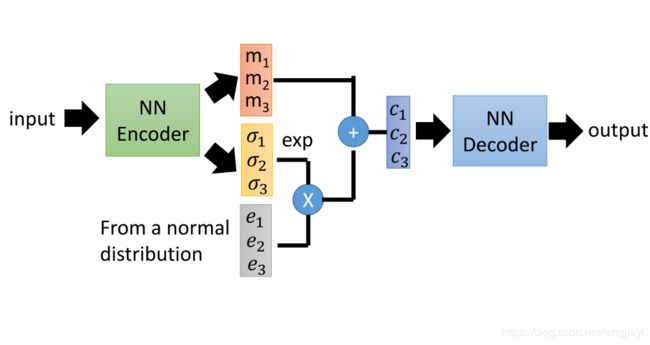
​ \qquad VAE(Variational Autoencoder)即变分自动编码器，在AutoEncoder的基础上做了一些修改使其成为生成模型。模型结构如下：

即编码器会产生两个相同维度的输出向量$m,\sigma$，其中m可以理解为均值，$\sigma$可以理解为噪声的方差为了取正因此加上了指数，$e$则是随机产生的符合正态分布的噪声。因此decoder的输入即为：
$$z=m+e^{\sigma }\times e$$
​ \qquad 新的编码层输出可以看作encoder实际上产生的是在编码空间的一个小区域，大小由$\sigma$控制，这个空间内的编码对应该样本的概率符合高斯分布。（高斯混合模型）

在训练模型时，优化目标除了重构误差外增加了一项：
$$min\sum exp({\sigma }_i)-(1+{\sigma }_i)+m_i^2$$
可以理解为前半部分$exp(\sigma )-(1+\sigma )$保证了方差不会太小（取最小值时${\sigma }_i$=1），后半部分$m^2$则相当于是对编码输出进行了L2规范化防止过拟合。

Warning Of Math

​ \qquad 如上文所说，假设样本空间的概率分布函数为$P(x)$，编码空间符合高斯分布，则对于每一个编码空间的采样z都对应一个高斯函数，这些高斯函数共同组成了$P(x)$，如下图：

即
$$P(x)={\int }_{z}P(z)P(x|z)dz$$
则可以通过训练一个神经网络为每一个z产生高斯函数的均值和方差$\mu (z),\sigma (z)$，优化目标为$maxP(x)$，即重构效果最好，可以对应decoder：

​ \qquad 反过来，存在另一个函数$q(z|x)$产生x的编码在编码空间的高斯函数$N({\mu }^{\prime }(x),{\sigma }^{\prime }(x))$，对应encoder，同样可以通过神经网络训练：

对于优化目标：
$$\begin{gathered} L=\sum _{x}logP(x) \\ logP(x)=logP(x){\int }_{z}q(z|x)dz={\int }_{z}q(z|x)logP(x)dz \\ ={\int }_{z}q(z|x)log(\frac{P(z,x)}{P(z|x)})dz={\int }_{z}q(z|x)log(\frac{P(z,x)}{q(z|x)}\frac{q(z|x)}{P(z|x)})dz \\ ={\int }_{z}q(z|x)log(\frac{P(z|x)P(z)}{q(z|x)})dz+{\int }_{z}q(z|x)log(\frac{q(z|x)}{P(z|x)})dz \\ =L_b+KL(q(z|x)||P(z|x)) \end{gathered}$$
其中KL divergence表示两个分布的相似程度，当同分布时取最小值0。因此$L_b$是优化下界，理想情况时输入等于输出，KL=0

$$\begin{gathered} L_b={\int }_{z}q(z|x)log(\frac{P(z|x)P(z)}{q(z|x)})dz \\ ={\int }_{z}q(z|x)log(\frac{P(z)}{q(z|x)})dz+{\int }_{z}q(z|x)logP(z)dz \\ =-KL(q(z|x)||P(z))+{\int }_{z}q(z|x)logP(z)dz \end{gathered}$$

\qquad 对于前一项，$max{L}_b\Rightarrow minKL(q(z|x)||P(z))$，即使得encoder产生的z分布和编码空间的高斯分布接近，并且：
$$minKL(q(z|x)||P(z))\iff minexp(\sigma )-(1+\sigma )+m^2$$
即之前添加的优化目标。

\qquad 对于后一项，$\int q(z|x)logP(x|z)dz=E_{q(z|x)}[logP(x|z)]$，即在z由x产生的条件下对z产生的输出概率求期望，可以理解为编码-解码后的概率：

因此对后一项取最大值即使得编码-解码后的输出和输入尽可能相似，即降低重构误差，显然高斯函数取中轴得时候概率最大。

2.2 数据集

​ \qquad 数据采用了这篇文章提供的动漫人脸图片。

\qquad 原文提供了五万多张96*96的动漫人脸，我随机选取了1044个图片，并且缩放到了30*30大小。本来我使用了143种常用颜色对原图进行了编码，不过再次出现了之前Pokemon数据集编码后由于编码颜色不连续导致输入维度过高的问题，我尝试使用VAE进行训练，结果收敛速度十分缓慢，并且效果也差强人意。

\qquad 为了加速训练，我将1044张彩色图片转化为255色彩空间种的灰度图储存在数组中。由于灰度值为连续的，因此可以直接使用原图作为输入，即输入输出维度为30*30

2.3 构建网络

\qquad 我分别使用了全连接层和卷积层构造了两种网络，显然卷积层的参数更少，但是在实际训练时发现效果不如全连接层。

全连接层网络

class VAE(nn.Module):
	def __init__(self):
		super(VAE, self).__init__()
		self.ZDim=10
		self.encoder = nn.Sequential(
			nn.Linear(30*30,512),
			nn.ReLU(True),
			nn.Linear(512,96),
			nn.ReLU(True),
			nn.Linear(96,25),
			)
		self.fcmu=nn.Linear(25,self.ZDim)
		self.fcvar=nn.Linear(25,self.ZDim)
		self.decoder = nn.Sequential(
			nn.Linear(self.ZDim,25),
			nn.ReLU(True),
			nn.Linear(25,96),
			nn.ReLU(True),
			nn.Linear(96,512),
			nn.ReLU(True),
			nn.Linear(512,30*30),
			)
	def reparameterize(self, mu, logvar):
		#z=exp(loavar)*eps+mu
		eps = torch.randn(mu.size(0),mu.size(1))
		z=mu+eps*torch.exp(logvar/2)
		return z

	def forward(self, x):
		x=self.encoder(x)
		logvar=self.fcvar(x)
		mu=self.fcmu(x)
		z=self.reparameterize(mu,logvar)
		#return reconstructed sample, mu and logvar
		return self.decoder(z),mu,logvar


#需要使用自定义的损失函数进行训练
def loss_func(recon_x, x, mu, logvar):
	BCE = criterion(recon_x.float(), x.float())
	#Minimize{1+logvar-(mu)^2-exp(logvar)}
	KLD=-0.5* torch.sum(1+logvar-mu.pow(2)-logvar.exp())
	return BCE+KLD

使用卷积层的网络

class VAE(nn.Module):
	def __init__(self):
		super(VAE, self).__init__()
		self.ZDim=10
		self.encoder = nn.Sequential(
			nn.Conv2d(1,10,5,stride=1,padding=0), #30*30=>10*26*26
			nn.ReLU(True),
			nn.MaxPool2d(2,2),	#10*26*26=>19*13*13
			nn.Conv2d(10,5,5,stride=2,padding=1), #10*13*13=>5*6*6
			nn.ReLU(True),
			nn.MaxPool2d(2,2),  #3*4*4=>5*3*3
			)
		self.fcmu=nn.Linear(5*3*3,self.ZDim)
		self.fcvar=nn.Linear(5*3*3,self.ZDim)
		self.fc2=nn.Linear(self.ZDim,5*3*3)
        #这里偷懒了没有用MaxUnpool2d
		self.decodeConv = nn.Sequential(
			nn.ConvTranspose2d(5,10,4,stride=2,padding=0), #5*3*3=>5*6*6
			nn.ReLU(),
			nn.ConvTranspose2d(10,3,6,stride=3,padding=0), #5*6*6=>10*13*13
			nn.ReLU(),
			nn.ConvTranspose2d(3,1,4,stride=1,padding=0), #10*26*26=>1*30*30
			nn.ReLU(),
			)
	def decoder(self,x):
		x=self.fc2(x)
		x=x.view(x.shape[0],5,3,3)
		x=self.decodeConv(x)
		return x

	def reparameterize(self, mu, logvar):
		#z=exp(loavar)*eps+mu
		eps = torch.randn(mu.size(0),mu.size(1))
		z=mu+eps*torch.exp(logvar/2)
		return z

	def forward(self, x):
		x=self.encoder(x)
		x=x.view(x.shape[0],45)
		logvar=self.fcvar(x)
		mu=self.fcmu(x)
		z=self.reparameterize(mu,logvar)
		#return reconstructed sample, mu and logvar
		return self.decoder(z),mu,logvar

2.4 训练结果

\qquad 相比于GAN，VAE得生成结果会很模糊，并且可能会出现比较明显的噪点。我在实际训练时发现Conv生成得图片更模糊，可能是因为没有加入反向池化。

编码-解码

上图是全连接的VAE对18张随机的人脸编码-解码后的结果，可以看出对颜色的还原比较精准，但是对人脸倾斜角度的还原不是很好。

这张则是加入卷积层后的结果，有的人脸（最后一行第三张）已经模糊到无法辨认了。

生成

\qquad 上图是随机选取两个样本编码及其高维线段中间的七个等分点产生的脸，两端是输入图片，可以看到人脸的发色逐渐变浅，人脸的朝向也从向右逐渐转为向左。

\qquad 上图则是在编码空间使用numpy.random.normal随机产生的一些人脸，可以看到7.png出现了之前所说的明显噪点，而21则出现了较明显的问题。

编码空间

我试图解读每一个维度的作用，所以按照编码空间大小产生了十个序列的图片，分别对应十个维度的变化，如下图：

事实证明这种非条件的学习不能韩浩的解读大部分维度。

• 第一、二、六、八、十维看起来就对生成结果没有什么影响。

• 第三维度增加时头发变短

• 第四维增加时阴影从左边跑到右边，不过不知道这是什么

• 第九维增加时头发颜色变浅

• 大部分维度都对脸的朝向有影响

2.5 进一步训练

​ \qquad 看到训练结果以后觉得黑白图片不是很好看，并且很糊，于是就想能不能补救一下，所以我又建立了一个网络将这些训练成的灰度图转换回彩色图片，并且试图去除一些噪点。

2.5.1 网络结构

​ \qquad 其实这个网络就是随手搭建的，所以没有什么技巧可言。

​ \qquad 大概思路就是先用反卷积映射到高维空间，再降维变成三个通道图片。训练的时候为了只完成着色，防止直接修改原图增加了和原图对比的MSELoss，而且在输入时增加了高斯噪声防止过拟合。代码如下：

class StackNN(nn.Module):
	def __init__(self):
		super(StackNN, self).__init__()
		self.remap = nn.Sequential(
			nn.ConvTranspose2d(1,10,5,stride=2,padding=0),
			nn.ReLU(),
			nn.Conv2d(10,5,5),#3*59*59
			nn.ReLU(),
			)
		self.fc = nn.Sequential(
			nn.Linear(5*59*59,5*30*30),
			nn.Linear(5*30*30,3*30*30),
			)
	def forward(self, x):
        #加入高斯噪声
		eps = torch.randn(x.size(0),x.size(1),x.size(2),x.size(3))
		x=x+eps
		x=self.remap(x)
		x=x.view(x.shape[0],5*59*59)
		x=self.fc(x)
		x=x.view(x.shape[0],3,30,30)
		return x


def loss_func(recon_x, x, target):
	colorloss = criterion(recon_x.float(), target.float())
	gray = (recon_x[:,0,:,:]*30+recon_x[:,1,:,:]*59+recon_x[:,2,:,:]*11)/100
	gray = gray.view(gray.shape[0],1,30,30)
	originloss = criterion(gray.float(),x.float()/255)
    #这一步是将颜色映射到[0,1]实数域，为两部分误差赋相同的权重
	return colorloss+originloss

2.5.2 训练结果

​ \qquad 使用最基本的MSELoss和Adam更新梯度，我迭代了40个epoch之后效果已经出来了，对之前随机产生的数据进行着色结果如下：

​ \qquad 可以看到脸部、眼睛和头发都有很好的上色，不过由于VAE产生的结果背景都很模糊所以着色后依然很模糊。

结合之前对编码空间的分析重新着色后：

源码见github