三维重建（三）相机参数标定与光束平差法（Bundle Adjustment）

一、针孔成像模型涉及到的坐标系

由于相机的参数总数相对于某种光学模型而言的，这里用到的比较广泛的光学模型就是小孔成像的模型，下面针对小孔成像的光学模型涉及到的坐标系一一介绍。

1、世界坐标系

世界坐标系即为三维空间中物体的坐标，用 (Xw,Yw,Zw) 表示，如下图所示：

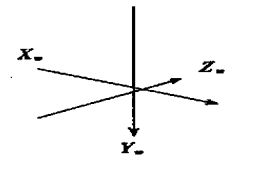
2、摄像机坐标系

摄像机坐标系用 (Xc,Yc,Zc) 表示， Xc , Yc 与图像横轴和纵轴平行，以相机的光心 O 为坐标原点， Zc 轴为相机的主光轴。

3、图像坐标系

图像坐标系以图像的中心为原点，水平方向为 X 轴，竖直方向为 Y 轴，用 (x,y) 表示，这里需要注意的是图像坐标系的单位为 mm 。

4、像素坐标系

像素坐标系与图像坐标系类似，只不过原点在图像的左上角，水平向右为 X 轴正方向，竖直向下为 Y 轴正方向，用 (u,v) 表示。注意，这里顾名思义，像素坐标系是以像素为单位的。
四种坐标系的关系如下图所示：

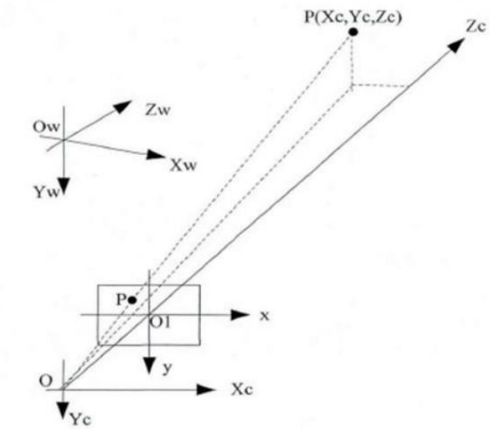
5、坐标系之间的关系

像素坐标系与图像坐标系的关系为：

⎡⎣⎢uv1⎤⎦⎥=⎡⎣⎢⎢⎢⎢⎢1dx0001dy0u0v01⎤⎦⎥⎥⎥⎥⎥⎡⎣⎢xy1⎤⎦⎥

其中 dx 和 dy 分别为表示单个像素点的规格， (u0,v0) 表示在像素坐标系中图像的中心的坐标。

图像坐标系与摄像机坐标系的关系为：

Zc⎡⎣⎢xy1⎤⎦⎥=⎡⎣⎢f000f0001000⎤⎦⎥⎡⎣⎢⎢⎢XcYcZc1⎤⎦⎥⎥⎥

其中f为摄像机镜头的焦距。
相对于世界坐标系，相机坐标系主要有平移和旋转两种操作，那么相机坐标系与世界坐标系的关系为：

⎡⎣⎢⎢⎢XcYcZc1⎤⎦⎥⎥⎥=[R0Tt1]⎡⎣⎢⎢⎢XwYwZw1⎤⎦⎥⎥⎥

其中 R 为旋转矩阵， t 为平移矩阵。
那么，像素坐标系与世界坐标系的关系一目了然，为：

Zc⎡⎣⎢uv1⎤⎦⎥=⎡⎣⎢⎢⎢⎢⎢1dx0001dy0u0v01⎤⎦⎥⎥⎥⎥⎥⎡⎣⎢f000f0001000⎤⎦⎥[R0Tt1]⎡⎣⎢⎢⎢XwYwZw1⎤⎦⎥⎥⎥=⎡⎣⎢ax000ay0u0v01000⎤⎦⎥[R0Tt1]⎡⎣⎢⎢⎢XwYwZw1⎤⎦⎥⎥⎥=M1M2⎡⎣⎢⎢⎢XwYwZw1⎤⎦⎥⎥⎥=M⎡⎣⎢⎢⎢XwYwZw1⎤⎦⎥⎥⎥

其中 M1 为相机的内参数矩阵， M2 为外参数矩阵， M 为投影矩阵。相机参数标定即为求出内参数矩阵和外参数矩阵。

二、相机参数的标定

由上可知，相机的内部参数矩阵中，主要的未知数为相机的焦距 f ，这个可以从图像的exif信息中得到，如下图所示：

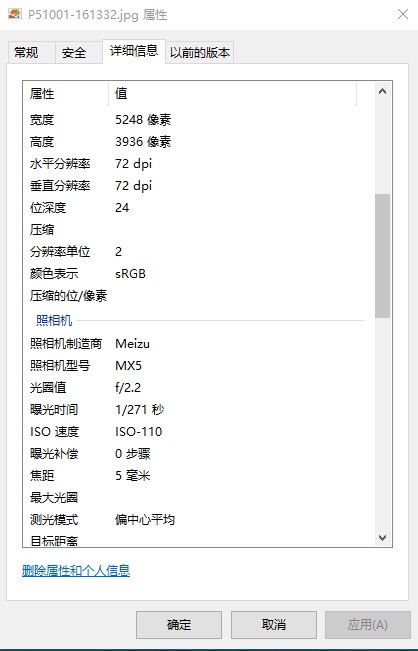
基础矩阵 F 表示的是空间中一点 P 在不同视角的相机下的像点在分别的摄像机坐标下的关系。
即空间中一点 P 在相机a的像点在a摄像机坐标为 PCa=⎡⎣⎢xcaycazca⎤⎦⎥
与 P 在另一台相机b的像点在b摄像机坐标系下 PCb=⎡⎣⎢⎢xcbycbzcb⎤⎦⎥⎥
的关系为 PCaFPCb=0
本质矩阵 E 表示的是空间中一点 P 在不同视角的相机下的像素点在不同像素坐标系下的关系。
即空间中一点 P 在相机a的像点在a的像素坐标系下坐标 Pa=⎡⎣⎢uava1⎤⎦⎥
与 P 在相机b的像点在b的像素坐标系下坐标 Pb=⎡⎣⎢ubvb1⎤⎦⎥ 的关系为 PaEPb=0
则可知基础矩阵和本质矩阵之间的关系为 E=MT1lFM1r ，这里 M1 为上面得到的相机的内部参数矩阵， l和r 表示左和右，因为在大多是实验中使用的是同一个相机，因此左右的内部参数矩阵经常是一样的。
这里讲这么多是为了得到本质矩阵 E ，为什么要得到它呢，当时是因为有用了（废话），下面继续讲本质矩阵 E 的作用。
本质矩阵 E 其实是可以表示为两个相机的相对旋转角度和平移向量的的关系，即 E=[t]xR ，这里R是两个相机的相对旋转矩阵，t为两个相机的相对平移向量。这里有 [t]x 的定义如下所示：

[t]x=⎡⎣⎢0tz−ty−tz0txty−tz0⎤⎦⎥

（加一点私货，我觉得这里的 R 和 t 与摄像机坐标系到世界坐标系转换时用到的 R 和 t 是不一样的，前者是两个摄像机坐标系的相对位置关系，而后者则是摄像机坐标系到世界坐标系的位置关系。
那么怎么确定物体的世界坐标系的坐标呢？我觉得可能是先确定好一个摄像机坐标系在世界坐标系中的表示形式，然后通过摄像机坐标系之间的相对位置关系确定其他的摄像机坐标系在世界坐标系的表现形式。不过我还没有查到具体的资料，因此也不敢确定，我暂且先这么理解，如果有错误，希望看到的能不吝指正。）

三、光束平差法（Bundle Adjustment）

简单的介绍一下光束平差法，具体我还没有深入的研究，只是明白他的大体的工作方式。
BundleAdjustment可以将所观测的图像位置和预测的图像位置点进行最小error的映射（匹配），由很多非线性函数的平方和表示（error）。因此，最小化error由非线性最小二乘法实现。
由上面我们可以得到一系列的相机的参数 [R1|t1],[R2|t2]… 和一系列的特征点的在世界坐标系下的坐标 X1,X2,X3… ，我们得到的这些可能会因为噪声等出现误差，那，我们要做的就是最小化误差，即进行下面的操作

min∑i∑j(xji−M[Ri|ti]Xj)

，这里 xji 表示第i幅图像的第j个特征点，即 Xj 在第i幅图像上的投影。