数据结构学习之路-第三章:栈的应用
【 声明:版权所有,转载请标明出处,请勿用于商业用途。 联系信箱:[email protected]】
前言:
前面已经介绍过栈的相关操作的具体实现,那么现在就按照书上的几个例子来具体讲一下栈的具体用处。
没有看之前我写的栈的实现的同学可以去看:传送门在这里哟
因为这里要用到我前面那篇博文中的函数,我都统一归集在一个头文件中,也就是下面的"my_stack.c"
那么接下来让我们进入正题吧。
注:
本文仅代表博主本人的一些浅显的见解,欢迎大家评论学习,共同创造出一个良好的环境
对于一些问题,博主会尽量为大家解答,但是如果有疑问没有及时回答的,也希望其他热心人心帮忙解决,鄙人不胜感激。
1.数制转换
数值转换就是一个取模之后然后逆向输出的过程,这个过程就是一个最经典的先进后出的操作,也就是我们将要使用的栈的原理。
#include"my.h" //包含所有必须头文件
#include"my_stack.c" //包含栈的相关定义与操作
void conversion()
{
//操作结果:对于输入的任意一个非负10进制整数,打印输出与其等值的16进制数
SqStack s;
unsigned n; //非负整数
SElemType e;
InitStack(&s); //初始化栈
printf("请输入非负整数 n=");
scanf("%u",&n); //输入非负十进制整数n
while(n) //当n不等于0
{
Push(&s,n%16);//入栈n除以16的余数(16进制的低位)
n=n/16;
}
while(!StackEmpty(s)) //当栈不空
{
Pop(&s,&e); //弹出栈顶元素且赋值给e
if(e<=9)
printf("%d",e);
else
printf("%c",e+55);
}
printf("\n");
}
int main()
{
conversion();
return 0;
}
2.括号匹配
对于多重括号嵌套的问题,我们都知道对于一个右括号而言,它仅仅只会与离它最近的左括号匹配,因此我们可以对整个字符串进行遍历,一旦遇到左括号,可以直接压入栈内,一旦遇到右括号,我们则需要将栈顶的左括号弹出并判断此时弹出的左括号与这个右括号是否匹配,一旦不匹配,那么整个字符串的括号必然是不匹配的。
#include"my.h" //包含所有必须头文件
#include"my_stack.c" //包含栈的相关定义与操作
void check()
{
//操作结果:对于输入的任意一个字符串,检验括号是否配对
SqStack s;
SElemType ch[80],*p,e;
if(InitStack(&s)) //初始化栈成功
{
printf("请输入表达式\n");
gets(ch);
p=ch;
while(*p) //没到串尾
switch(*p)
{
case '(':
case '[':
Push(&s,*p++);
break; //左括号入栈,且p++
case ')':
case ']':
if(!StackEmpty(s)) //栈不空
{
Pop(&s,&e); //弹出栈顶元素
if(*p==')'&&e!='('||*p==']'&&e!='[') //弹出的栈顶元素与*p不配对
{
printf("左右括号不配对\n");
exit(ERROR);
}
else
{
p++;
break; //跳出switch语句
}
}
else //栈空
{
printf("缺乏左括号\n");
exit(ERROR);
}
default:
p++; //其它字符不处理,指针向后移
}
if(StackEmpty(s)) //字符串结束时栈空
printf("括号匹配\n");
else
printf("缺乏右括号\n");
}
}
int main()
{
check();
return 0;
}
3.行编辑程序
#include"my.h" //包含所有必须头文件
#include"my_stack.c" //包含栈的相关定义与操作
FILE *fp;
Status copy(SElemType c)
{
//将字符c送至fp所指的文件中
fputc(c,fp);
return OK;
}
void LineEdit()
{
//利用字符栈s,从终端接收一行并送至调用过程的数据区。
SqStack s;
char ch,c;
InitStack(&s);
printf("请输入一个文本文件,^Z结束输入:\n");
ch=getchar();
while(ch!=EOF)
{
while(ch!=EOF&&ch!='\n')
{
switch(ch)
{
case '#':
Pop(&s,&c);
break; //仅当栈非空时退栈
case '@':
ClearStack(&s);
break; //重置s为空栈
default :
Push(&s,ch); //有效字符进栈
}
ch=getchar(); //从终端接收下一个字符
}
StackTraverse(s,copy); //将从栈底到栈顶的栈内字符传送至文件
ClearStack(&s); //重置s为空栈
fputc('\n',fp);
if(ch!=EOF)
ch=getchar();
}
DestroyStack(&s);
}
int main()
{
fp=fopen("ED.DAT","w"); //在当前目录下建立ED.DAT文件,用于写数据
if(fp) // 如已有同名文件则先删除原文件
{
LineEdit();
fclose(fp); //关闭fp所指的文件
}
else
printf("建立文件失败!\n");
return 0;
}
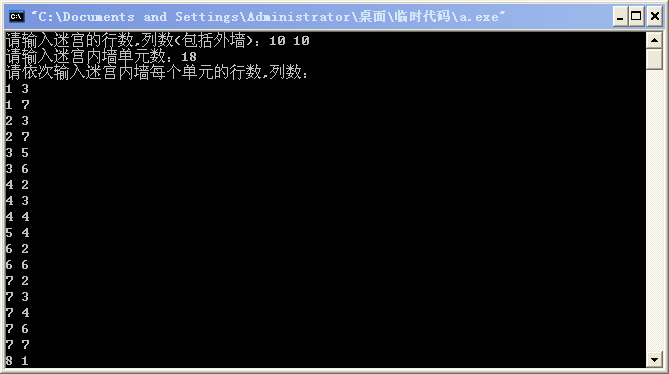
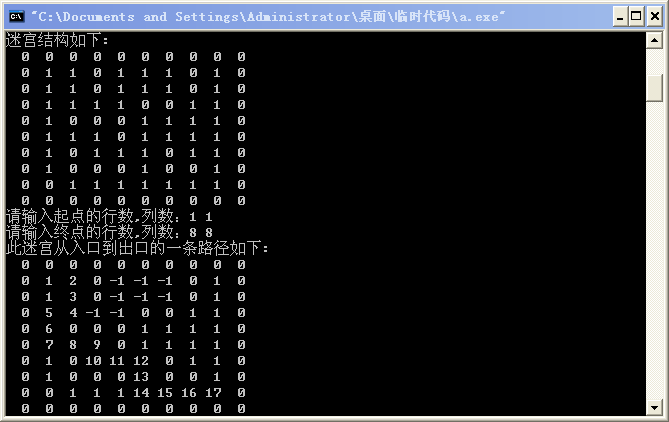
4.迷宫求解
typedef struct //迷宫坐标位置类型
{
int x; //行值
int y; //列值
} PosType;
#define MAXLENGTH 50 //设迷宫的最大行列值
typedef int MazeType[MAXLENGTH][MAXLENGTH]; //迷宫数组[行][列]
MazeType m; //迷宫数组
int curstep=1; //当前足迹,初值为1
typedef struct //栈的元素类型
{
int ord; //通道块在路径上的"序号"
PosType seat; //通道块在迷宫中的"坐标位置"
int di; //从此通道块走向下一通道块的"方向"(0~3表示东~北)
} SElemType;
#include"my.h" //包含所有必须头文件
#include"my_stack.c" //包含栈的相关定义与操作
//定义墙元素值为0,可通过路径为1,不能通过路径为-1,通过路径为足迹
Status Pass(PosType b)
{
//操作结果:当迷宫m的b点的序号为1(可通过路径),return OK; 否则,return ERROR
if(m[b.x][b.y]==1)
return OK;
else
return ERROR;
}
void FootPrint(PosType a)
{
//操作结果:使迷宫m的a点的序号变为足迹(curstep)
m[a.x][a.y]=curstep;
}
PosType NextPos(PosType c,int di)
{
//操作结果:根据当前位置及移动方向,返回下一位置
PosType direc[4]= {{0,1},{1,0},{0,-1},{-1,0}}; //{行增量,列增量}
//移动方向,依次为东南西北
c.x+=direc[di].x;
c.y+=direc[di].y;
return c;
}
void MarkPrint(PosType b)
{
//使迷宫m的b点的序号变为-1(不能通过的路径)
m[b.x][b.y]=-1;
}
Status MazePath(PosType _start,PosType _end)
{
//操作结果:若迷宫maze中存在从入口start到出口end的通道,则求得一条存放在栈中(从栈底到栈顶),并返回TRUE;否则返回FALSE
SqStack S;
PosType curpos;
SElemType e;
InitStack(&S);
curpos=_start;
do
{
if(Pass(curpos))
{
//当前位置可以通过,即是未曾走到过的通道块
FootPrint(curpos); //留下足迹
e.ord=curstep;
e.seat.x=curpos.x;
e.seat.y=curpos.y;
e.di=0;
Push(&S,e); //入栈当前位置及状态
curstep++; //足迹加1
if(curpos.x==_end.x&&curpos.y==_end.y) //到达终点(出口)
return TRUE;
curpos=NextPos(curpos,e.di);
}
else
{
//当前位置不能通过
if(!StackEmpty(S))
{
Pop(&S,&e); //退栈到前一位置
curstep--;
while(e.di==3&&!StackEmpty(S)) //前一位置处于最后一个方向(北)
{
MarkPrint(e.seat); //留下不能通过的标记(-1)
Pop(&S,&e); //退回一步
curstep--;
}
if(e.di<3) //没到最后一个方向(北)
{
e.di++; //换下一个方向探索
Push(&S,e);
curstep++;
curpos=NextPos(e.seat,e.di); //设定当前位置是该新方向上的相邻块
}
}
}
}
while(!StackEmpty(S));
return FALSE;
}
void Print(int x,int y)
{
//操作结果:输出迷宫的解
int i,j;
for(i=0; i运行样例:
5.表达式求解
typedef char SElemType;
#include"my.h"
#include"my_stack.c"
SElemType Precede(SElemType t1,SElemType t2)
{
//操作结果:根据教科书表3.1,判断两符号的优先关系
SElemType f;
switch(t2)
{
case '+':
case '-':
if(t1=='('||t1=='=')
f='<';
else
f='>';
break;
case '*':
case '/':
if(t1=='*'||t1=='/'||t1==')')
f='>';
else
f='<';
break;
case '(':
if(t1==')')
{
printf("ERROR1\n");
exit(ERROR);
}
else
f='<';
break;
case ')':
switch(t1)
{
case '(':
f='=';
break;
case '=':
printf("ERROR2\n");
exit(ERROR);
default:
f='>';
}
break;
case '=':
switch(t1)
{
case '=':
f='=';
break;
case '(':
printf("ERROR2\n");
exit(ERROR);
default:
f='>';
}
}
return f;
}
Status In(SElemType c)
{
//操作结果:判断c是否为运算符
switch(c)
{
case'+':
case'-':
case'*':
case'/':
case'(':
case')':
case'=':
return TRUE;
default:
return FALSE;
}
}
SElemType Operate(SElemType a,SElemType theta,SElemType b)
{
SElemType c;
switch(theta)
{
case'+':
c=a+b;
break;
case'-':
c=a-b;
break;
case'*':
c=a*b;
break;
case'/':
c=a/b;
}
return c;
}
SElemType EvaluateExpression()
{
//操作结果:算术表达式求值的算符优先算法。设OPTR和OPND分别为运算符栈和运算数栈
SqStack OPTR,OPND;
SElemType a,b,d,x,theta;
char c; //存放由键盘接收的字符串
char z[6]; //存放整数字符串
int i;
InitStack(&OPTR); //初始化运算符栈
Push(&OPTR,'='); //=是表达式结束标志
InitStack(&OPND); //初始化运算数栈
c=getchar();
GetTop(OPTR,&x);
while(c!='='||x!='=')
{
if(In(c)) //是7种运算符之一
switch(Precede(x,c))
{
case'<':
Push(&OPTR,c); //栈顶元素优先权低
c=getchar();
break;
case'=':
Pop(&OPTR,&x); //脱括号并接收下一字符
c=getchar();
break;
case'>':
Pop(&OPTR,&theta); //退栈并将运算结果入栈
Pop(&OPND,&b);
Pop(&OPND,&a);
Push(&OPND,Operate(a,theta,b));
}
else if(c>='0'&&c<='9') //c是操作数
{
i=0;
do
{
z[i]=c;
i++;
c=getchar();
}
while(c>='0'&&c<='9');
z[i]=0;
d=atoi(z); //将字符串数组转为整型存于d
Push(&OPND,d);
}
else //c是非法字符
{
printf("ERROR3\n");
exit(ERROR);
}
GetTop(OPTR,&x);
}
GetTop(OPND,&x);
return x;
}
int main()
{
printf("请输入算术表达式,负数要用(0-正数)表示,并以=结束\n");
printf("%d\n",EvaluateExpression());
return 0;
}
运行样例:
6.递归实现汉诺塔
#include
int c=0; //全局变量,搬动次数
void _move(char x,int n,char z)
{
printf("第%i步: 将%i号盘从%c移到%c\n",++c,n,x,z);
}
void hanoi(int n,char x,char y,char z)
{
//操作结果:将塔座x上按直径由小到大且自上而下编号为1至n的n个圆盘按规则搬到塔座z上。y可用作辅助塔座
if(n==1)
_move(x,1,z); //将编号为1的圆盘从x移到z
else
{
hanoi(n-1,x,z,y); //将x上编号为1至n-1的圆盘移到y,z作辅助塔
_move(x,n,z); //将编号为n的圆盘从x移到z
hanoi(n-1,y,x,z); //将y上编号为1至n-1的圆盘移到z,x作辅助塔
}
}
void main()
{
int n;
printf("3个塔座为a、b、c,圆盘最初在a座,借助b座移到c座。请输入圆盘数:");
scanf("%d",&n);
hanoi(n,'a','b','c');
}
总结:
书上栈的应用样例差不多就这些了,希望能够帮助大家更加理解栈是怎样的一回事。
那么下次,我们就会进入一个与栈类似却又不同的数据结构的学习,那就是队列。