无人驾驶一 协方差矩阵的几何意义
https://blog.csdn.net/guyuealian/article/details/68922981
样本各属性(维)均值:样本重心;
样本各属性间协方差:样本在各维间分布及相关性。对协方差矩阵进行特征变换,特征矩阵每列为特性向量=主坐标轴在原坐标系的投影(坐标)。
clear all
clc
X=[1 2;3 3;3 5;5 4;5 6;6 5;8 7;9 8] %样本矩阵:8个样本,每个样本2个特征
covX= cov(X) %使用cov函数求协方差矩阵
%% 按定义求协方差矩阵:(1)使用分量的方法,先求协方差,再组合成协方差矩阵
meanX=mean(X) %样本均值
varX=var(X) %样本方差
[Row Col]=size(X);
dimNum=Row; %s样本个数size(X,1)=8
dim1=X(:,1); %特征分量1
dim2=X(:,2); %而在分量2
c11=sum( (dim1-mean(dim1)) .* (dim1-mean(dim1)) ) / ( dimNum-1 );
c21=sum( (dim2-mean(dim2)) .* (dim1-mean(dim1)) ) / ( dimNum-1 );
c12=sum( (dim1-mean(dim1)) .* (dim2-mean(dim2)) ) / ( dimNum-1 );
c22=sum( (dim2-mean(dim2)) .* (dim2-mean(dim2)) ) / ( dimNum-1 );
C22=[c11,c12;c21,c22]%协方差矩阵
%% 或者(2)直接求协方差矩阵:
tempX= repmat(meanX,Row,1);
C22=(X-tempX)'*(X-tempX)/(dimNum-1)
%% 特征值分解协方差矩阵:
[V,D] =eigs(covX)
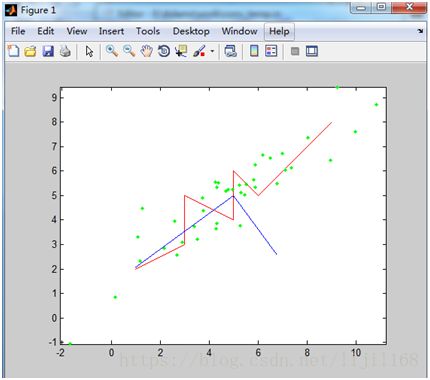
e1_point=meanX'+V(:,1)*5 %主坐标轴e1=e1_piont-meanX
e2_point=meanX'+V(:,2)*3 %主坐标轴e2=e2_piont-meanX
plot(X(:,1),X(:,2),'r')
hold on
axis equal
plot([meanX(1);e1_point(1)],[meanX(2);e1_point(2)])
plot([meanX(1);e2_point(1)],[meanX(2);e2_point(2)])
Xtemp=mvnrnd(meanX,covX,40) %生成同分布的样本点
plot(Xtemp(:,1),Xtemp(:,2),'.g')
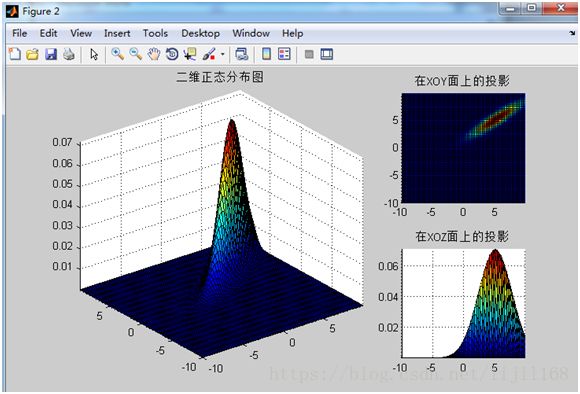
%% 绘制二维正态分布图
[X,Y]=meshgrid(-10:0.3:10,-10:0.3:10);%在XOY面上,产生网格数据
p=mvnpdf([X(:) Y(:)],meanX,covX);%求取联合概率密度,相当于Z轴
p=reshape(p,size(X));%将Z值对应到相应的坐标上
figure
set(gcf,'Position',get(gcf,'Position').*[1 1 1.3 1])
subplot(2,3,[1 2 4 5])
surf(X,Y,p),axis tight,title('二维正态分布图')
subplot(2,3,3)
surf(X,Y,p),view(2),axis tight,title('在XOY面上的投影')
subplot(2,3,6)
surf(X,Y,p),view([0 0]),axis tight,title('在XOZ面上的投影')
covX =
7.1429 4.8571
4.8571 4.0000
meanX =
5 5
V =
-0.8086 0.5883
-0.5883 -0.8086
D =
10.6764 0
0 0.4664