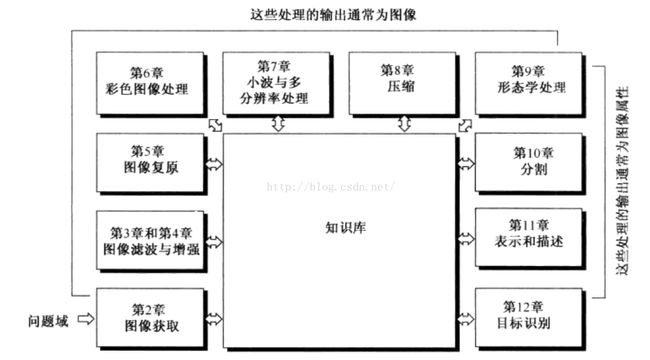
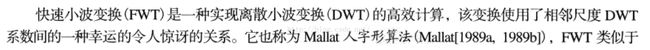《数字图像处理》笔记

第一章：绪论

第二章：数字图像基础

2.3.3  传感器阵列获取图像

2.3.5  取样和量化   (8位的灰度级)

2.4.2  数字图像表示 

  矩阵形式   m*n

k比特灰度级图像

图像的大小

2.4.3  空间和灰度级分辨率

空间分辨率  m*n

2.4.5    放大和收缩图像

放大   过采样   收缩  欠采样 

如内插等操作

为了减小混淆效应，收缩前模糊一下图像，降低引起混淆的高频分量

2.5像素间的关系：

相邻像素

邻接性、连通性、区域和边界

距离  D8和D4

像素的线性与非线性操作

第三章   空间域图像增强

高度主观的过程

3.1   函数模型  s=t（r）正方形领域

3.2   基本的灰度变换

图像反转、对数变换（拓展被压缩的高值图像中的暗像素）

幂次变换（输入窄带暗值映射到宽带输出值 s =cr（y））

分段线性变换

对比拉伸（提高图像处理时的灰度级的动态范围）

灰度切割

位图切割

3.3  直方图处理

某一灰度级的概率值

使一幅图像的像素占有全部的灰度级并分布均匀，开发一函数，仅仅依靠输入图像的信息可自动达到这个效果。

直方图均衡化       直方图匹配

局部增强：图像小区域细节的局部增强

算术逻辑操作：图像减法、图像平均值、

空间滤波器基础：是系数值

3.6  平滑空间滤波器

模糊处理和减小噪声、去除图像中的琐碎细节

平滑线性（加权和非加权）

统计排序滤波器（非线性）：处理椒盐噪声

3.7  锐化空间滤波器

突出细节，空间微分来处理，增强了突变，消弱了灰度变化缓慢的区域

一阶微分，边缘提取；梯度法

二阶微分：拉普拉斯算子，数学推倒、

混合空间增强法：多种互补的图像增强技术综合运用。

第4章：频域图像增强

一维的傅里叶变换、二维DFT，傅里叶谱、相角、频率普；频率普的直流成分。

频域滤波基础：包含如下步骤：   h（u，v）称为滤波器

一些基本滤波器及其性质：低频决定图像在平滑区域中总体灰度级的显示，高频决定图像细节部分，如边缘和噪声。高通和低通

空间域滤波器和频域滤波器的对应，傅里叶变换对，冲击函数和卷积

空间滤波的系数与高通低通的关系

高斯函数的滤波，其变换与反变换均为实高斯函数。

4.3平滑的频域滤波器

低通及效果、巴特沃斯低通、高斯低通（没有振铃）

频域锐化滤波器

高通、巴特沃斯高通、高斯高通、拉普拉斯算子

第5章   图像复原

利用退化现象的某种先验知识来重复或复原被退化的图像。可以采用频域或空域的方式

噪声模型：空间和频率特性：

噪声的概率密度函数：高斯噪声、瑞利噪声，指数分布噪声、均匀分布噪声、脉冲噪声（椒盐噪声）

5.2.3  周期噪声

从传感器中得出噪声的参估计

5.3 只有噪声的空间滤波复原

均值滤波器：

统计排序滤波器：

自适应滤波器：性能好，复杂度高。考虑一点对其他点的影响，考虑一个区域内的统计特性。

5.4频域滤波消减周期噪声

带阻、带通，陷波、

5.5  线性、位置不变的退化

许多退化的类型可以近似表示为线性的位置不变过程

具有加性噪声的线性空间不变退化系统，可在空间域被模型化为退化函数（点扩散函数）与图像的卷积，并加上噪声，亦可在频域内表示为图像和退化函数变换的乘积然后加上噪声的变换。

5.6  估计退化函数

3种方法

5.8 最小均方误差滤波（维纳滤波）

综合退化函数和噪声统计特征2个方面进行复原处理的方法、效果展示

5.9约束最小二乘方滤波器

只要求噪声方差和均值的知识

5.10  几何均值滤波

5.11  几何变换

第6章  彩色图像处理

亮度、色调和色饱和度       色度图

彩色模型     rgb、cmy   cmyk   hsi

cmy和cmyk与rgb模型间的关系   rgb与hsi模型关系

伪彩色处理  ：  根据特定的准则对灰度值赋以彩色的处理

    强度分层   灰度级到彩色的转换

6.4  全彩色图像处理基础

        彩色像素实际上是一个向量：单独的彩色分量的处理结果并不总等于在彩色向量空间的直接处理。

6.5  彩色变换      单一彩色模型范围内

     补色、增强图像的暗区域、彩色分层    色调和彩色矫正、直方图处理：均匀拓展彩色强度，保留彩色本身不变

6.6  平滑和尖锐化    基于周围像素的特点进行改进处理

      彩色图像平滑       彩色图像尖锐化（拉普拉斯方法）

6.7  彩色分割

  hsi彩色空间分割（饱和度为依据）     rgb向量空间（分割出特殊颜色区域）

  彩色边缘检测 （针对向量拓展梯度的概念）  彩色图像的噪声（）不同模型中噪声的转移

第7章   小波变换和多分辨率处理

   不同于傅里叶变换，基于小波的变换、传统的傅里叶变换只提供了音符或频率信息，局部信息在变换过程中丢失了。

多分辨率理论，小波为分析基础，如图像金字塔。

某种分辨率下无法发现的特性在另一分辨率下将很容易被发现。   

从多分辨率的角度来解释小波

1、图像金字塔，子抽样和内插，残差金字塔。

子带编码：许多子带重组无失真得到重建原始图像，每个子带通过对输入进行带通滤波而得到，原始图像的重建可以通过内插滤波和叠加单个子带来完成

z变换对，调制矩阵h

完美重建滤波器族。如子带图像编码的二维4频段滤波器组p284

7.1.3   哈尔变换     其基函数是最简单的正交小波    其矩阵描述

7.2  多分辨率展开

    多分辨率分析（MRA）中，尺度函数被用于建立某一函数或图像的一系列近似值，相邻两近似值之间的近似度相差2倍。称为小波的附加函数用于对相邻近值之间的差异进行编码。

7.2.1   序列展开   7.2.2  尺度函数    展开函数集合，其中$（x）称为尺度函数

          简单的尺度函数需准信4个基本要求

7.2.3  小波函数

  

7.3   一维小波变换

7.4  快速小波变换

7.5   二维小波变换

7.6   小波包

第8章   图像压缩

图像压缩所解决的问题是减少表示数字图像时所需的数据量，基本原理是去除其中的冗余数据，实际上将二维像素阵列变换为一个在统计上无关联的数据集合。

8.1  基本知识   

压缩率等       编码冗余      心理视觉冗余

8。2   图像压缩模型  信道编解码、信源编解码

8.3   信息论要素

   基本编码定理

8.4   无误差压缩   压缩率（2-10）

需要变长编码：   霍夫曼编码、其他变长编码

8.5   有损压缩  （1:100）

有损预测编码

变换编码

小波编码

8.6   图像压缩标准

二值图像压缩标准

连续色调静止图像压缩标准    jpeg   jpeg2000

视频压缩标准

第9章   形态学图像处理

将数学形态学作为工具从图像中提取对于表达和描述区域形状有用的图像分量，比如边界、骨架以及凸壳等。

后面的

9.1集合论的知识

9.2   膨胀与腐蚀

   集合操作的拓展、

9.3  开操作和闭操作

9.4  击中或及不中变换    （形状检测的基本工具）

9.5  一些形态学的算法

 边界提取

区域填充

联通分量的提取

凸壳骨架等等

9.6  灰度级拓展

用前面的操作探讨基本的灰度级形态学算法

 膨胀与腐蚀

等等

10  图像分割

用传统 的方法和形态学的方法，2种

11  表示和描述