详解EM算法与混合高斯模型(Gaussian mixture model, GMM)

 　　最近在看晓川老（shi）师(shu)的博士论文，接触了混合高斯模型（Gaussian mixture model, GMM）和EM(Expectation Maximization)算法，不禁被论文中庞大的数学公式所吓退。本文通过查阅相关资料，在复杂巧妙的推理公式中融入了自己的理解，详细梳理了混合高斯模型和EM算法。

1 单高斯模型(Gaussian single model, GSM）

 　　简单回顾一下概率论讲过的高斯模型。
　　高斯模型是一种常用的变量分布模型，在数理统计领域有着广泛的应用（……好吧读了这么多年书没白费，教科书般的话语已植入骨髓）。一维高斯分布的概率密度函数如下：
$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{{(x-\mu )}^2}{2{\sigma }^2})\text{\hspace{1em}(1)}$$　
　　 $\mu$和${\sigma }^2$分别是高斯分布的均值和方差。
　　譬如将男生身高视为变量X, 假设男生的身高服从高斯分布，则$X\sim N(\mu ,{\sigma }^2)$，女生亦如此。只是男女生身高分布可能具有不同的均值和方差。图1是从谷歌图库中搜索到的男女生身高分布图，来源不清，个人觉得男生的均值身高虚高……四个记号分别表示0~3$\sigma$准则。

图1 男女生身高分布差异

 　　多维变量$X=(x_1,x_2,...x_n)$的联合概率密度函数为：
$$f(X)=\frac{1}{{(2\pi )}^{d/2}{\left|\Sigma \right|}^{1/2}}\exp [-\frac{1}{2}(X-u{)}^T{\Sigma }^{-1}(X-u)],X=(x_1,x_2...x_n)\text{\hspace{1em}(2)}$$
　　其中：
　　d：变量维度。对于二维高斯分布，有d=2;
　　 $u=\left(\begin{array}{l}{u}_1\\ u_2\\ ...\\ u_n\end{array}\right)$：各维变量的均值；
　　 $\Sigma$：协方差矩阵，描述各维变量之间的相关度。对于二维高斯分布，有：
$$\Sigma =\left[\begin{array}{cc}{\delta }_{11}& {\delta }_{12}\\ {\delta }_{21}& {\delta }_{22}\end{array}\right]\text{\hspace{1em}(3)}$$

图2 二维高斯数据分布

 　　图2是二维高斯分布产生的数据示例，参数设定为：$u=\left(\begin{array}{l}0\\ 0\end{array}\right),\Sigma =\left[\begin{array}{cc}1& 0.8\\ 0.8& 5\end{array}\right]$。关于二维高斯分布的参数设定对为高斯曲面的影响，这篇文章二维高斯分布（Two-dimensional Gaussian distribution）的参数分析有提及，主要是为了下文理解混合高斯分布做铺垫。服从二维高斯分布的数据主要集中在一个椭圆内部，服从三维的数据集中在一个椭球内部。

2 混合高斯模型（Gaussian mixture model, GMM）

2.1 为什么要有混合高斯模型

先来看一组数据。　
　　　　　
　　

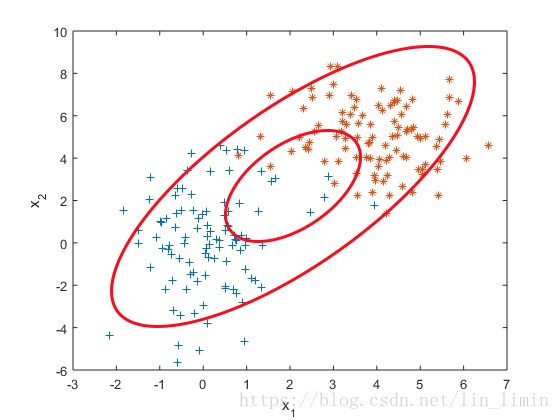
图3 混合高斯分布所产生数据

 　　如果我们假设这组数据是由某个高斯分布产生的，利用极大似然估计（后文还会提及）对这个高斯分布做参数估计，得到一个最佳的高斯分布模型如下。

图4 用单高斯模型对样本作分析不合理示意

 　　有什么问题吗？一般来讲越靠近椭圆的中心样本出现的概率越大，这是由概率密度函数决定的，但是这个高斯分布的椭圆中心的样本量却极少。显然样本服从单高斯分布的假设并不合理。单高斯模型无法产生这样的样本。
　　实际上，这是用两个不同的高斯分布模型产生的数据。

图5 混合高斯模型对样本作分析示意

 　　正当单高斯模型抓耳挠腮的时候，混合高斯模型就大摇大摆地进场了。它通过求解两个高斯模型，并通过一定的权重将两个高斯模型融合成一个模型，即最终的混合高斯模型。这个混合高斯模型可以产生这样的样本。
　　更一般化的描述为：假设混合高斯模型由K个高斯模型组成（即数据包含K个类），则GMM的概率密度函数如下：
$$p(x)=\sum _{k=1}^{K}p(k)p(x|k)=\sum _{k=1}^K{\pi }_{k}N(x|u_k,{\Sigma }_k)\text{\hspace{1em}(3)}$$
　　其中，$p(x|k)=N(x|u_k,{\Sigma }_k)$是第k个高斯模型的概率密度函数，可以看成选定第k个模型后，该模型产生x的概率；$p(k)={\pi }_k$是第k个高斯模型的权重，称作选择第k个模型的先验概率，且满足$\sum _{k=1}^K{\pi }_k=1$。
　　所以，混合高斯模型并不是什么新奇的东西，它的本质就是融合几个单高斯模型，来使得模型更加复杂，从而产生更复杂的样本。理论上，如果某个混合高斯模型融合的高斯模型个数足够多，它们之间的权重设定得足够合理，这个混合模型可以拟合任意分布的样本。

2.2 直观上理解混合高斯模型

 　　下面通过几张图片来帮助理解混合高斯模型。
　　首先从简单的一维混合高斯模型说起。
　

图6 一维混合高斯模型

 　　在图6中，y1,y2和y3分别表示三个一维高斯模型，他们的参数设定如图所示。y4表示将三个模型的概率密度函数直接相加，注意的是这并不是一个混合高斯模型，因为不满足$\sum _{k=1}^K{\pi }_k=1$的条件。而y5和y6分别是由三个相同的高斯模型融合生成的不同混合模型。由此可见，调整权重将极大影响混合模型的概率密度函数曲线。另一方面也可以直观地理解混合高斯模型可以更好地拟合样本的原因：它有更复杂更多变的概率密度函数曲线。理论上，混合高斯模型的概率密度函数曲线可以是任意形状的非线性函数。
　　下面再给出一个二维空间3个高斯模型混合的例子。
　

(a) 3个类别高斯分布截面轮廓线

(b) 混合高斯分布截面轮廓线

© 二维混合高斯分布概率密度函数图

图7 二维混合高斯模型

 　　(a) 图表示的是3个高斯模型的截面轮廓图，3个模型的权重系数已在图中注明，由截面轮廓图可知3个模型之间存在很多重叠区域。其实这也正是混合高斯模型所希望的。因为如果它们之间的重叠区域较少，那么生成的混合高斯模型一般较为简单，难以生成较为复杂的样本。
　　设定好了3个高斯模型和它们之间的权重系数之后，就可以确定二维混合高斯分布的概率密度函数曲面，如图©所示。图(b)是对于图©概率密度曲面的截面轮廓线。从图7也可以看出，整个混合高斯分布曲面相对比于单高斯分布曲面已经异常复杂。实际上，通过调整混合高斯分布的系数$(\pi ,\mu ,\Sigma )$，可以使得图©的概率密度曲面去拟合任意的三维曲面，从而采样生成所需要的数据样本。

3 极大似然估计(Maximum Likehood Estimate, MLE)（最大化对数似然函数）

● 最大化对数似然函数（log-likelihood function）的意义

 　　首先直观化地解释一下最大化对数似然函数要解决的是什么问题。
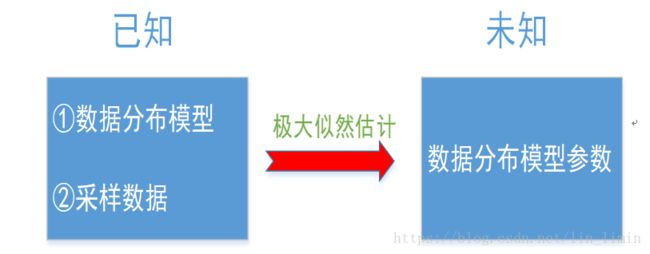
　　假设我们采样得到一组样本$y_t$,而且我们知道变量Y服从高斯分布（本文只提及高斯分布，其他变量分布模型类似），数学形式表示为$Y\sim N(\mu ,\Sigma )$。采样的样本如图8所示，我们的目的就是找到一个合适的高斯分布（也就是确定高斯分布的参数$\mu ,\Sigma$），使得这个高斯分布能产生这组样本的可能性尽可能大。
　

图8 最大化似然函数的意义

 　　那怎么找到这个合适的高斯分布呢（在图8中的表示就是1~4哪个分布较为合适）？这时候似然函数就闪亮登场了。
　　似然函数数学化：设有样本集$Y=y_1,y_2...y_N$。$p(y_n|\mu ,\Sigma )$是高斯分布的概率分布函数，表示变量$Y=y_n$的概率。假设样本的抽样是独立的，那么我们同时抽到这N个样本的概率是抽到每个样本概率的乘积，也就是样本集Y的联合概率。此联合概率即为似然函数：
$$L(\mu ,\Sigma )=L(y_1,y_2...y_N;\mu ,\Sigma )=\prod _{n=1}^{N}p(y_n;\mu ,\Sigma )\text{\hspace{1em}(4)}$$
　　对式子(4)进行求导并令导数为0（即最大化似然函数，一般还会先转化为对数似然函数再最大化），所求出的参数就是最佳的高斯分布对应的参数。
　　所以最大化似然函数的意义就是：通过使得样本集的联合概率最大来对参数进行估计，从而选择最佳的分布模型。
　　对于图8产生的样本用最大化似然函数的方法，最终可以得到序号1对应的高斯分布模型是最佳的模型。

4 EM算法（最大化Q函数）

4.1 为什么要有EM算法（EM算法与极大似然估计分别适用于什么问题）

● 尝试用极大似然估计的方法来解GMM模型

 　　解GMM模型，实际上就是确定GMM模型的参数$(\mu ,\Sigma ,\pi )$，使得由这组参数确定的GMM模型最有可能产生采样的样本。
　　先试试看用极大似然估计的方法来解GMM模型会出现什么样的问题。
　　如第3小节所述，要利用极大似然估计求解模型最重要的一步就是求出似然函数，即样本集出现的联合概率。而对于混合高斯模型，如何求解某个样本$y_t$的概率？显然我们得先知道这个样本来源于哪一类高斯模型，然后求这个高斯模型生成这个样本的概率$p(y_t)$。
　　但是问题来了：我们只有样本。不知道样本到底来源于哪一类的高斯模型。那么如何求解样本的生成概率$p(y_t)$？
　　先引入一个隐变量$\gamma$。它是一个K维二值随机变量，在它的K维取值中只有某个特定的元素${\gamma }_k$的取值为1，其它元素的取值为0。实际上，隐变量描述的就是：每一次采样，选择第k个高斯模型的概率，故有：
$$p({\gamma }_k=1)={\pi }_k\text{\hspace{1em}(5)}$$
　　当给定了$\gamma$的一个特定的值之后（也就是知道了这个样本从哪一个高斯模型进行采样），可以得到样本y的条件分布是一个高斯分布，满足：
$$p(y|{\gamma }_k=1)=N(y|{\mu }_k,{\Sigma }_k)\text{\hspace{1em}(6)}$$
　　而实际上，每个样本到底是从这K个高斯模型中哪个模型进行采样的，是都有可能的。故样本y的概率为：
$$p(y)={\sum }_{\gamma }p(\gamma )p(y|\gamma )=\sum _{\mathrm{k}=1}^K{\pi }_{k}N(y|{\mu }_k,{\Sigma }_k)\text{\hspace{1em}(7)}$$
　　样本集Y(n个样本点)的联合概率为：
$$L(\mu ,\Sigma ,\pi )=L(y_1,y_2...y_N;\mu ,\Sigma ,\pi )=\prod _{n=1}^{N}p(y_n;\mu ,\Sigma ,\pi )=\prod _{n=1}^N\sum _{\mathrm{k}=1}^K{\pi }_{k}N(y_n|{\mu }_k,{\Sigma }_k)\text{\hspace{1em}(8)}$$
　　对数似然函数表示为：
$$\ln L(\mu ,\Sigma ,\pi )=\sum _{n=1}^N\ln \sum _{\mathrm{k}=1}^K{\pi }_{k}N(y_n|{\mu }_k,{\Sigma }_k)\text{\hspace{1em}(9)}$$
　　好了，然后求导，令导数为0，得到模型参数$(\mu ,\Sigma ,\pi )$。
　　貌似问题已经解决了，喜大普奔。
　　然而仔细观察可以发现，对数似然函数里面，对数里面还有求和。实际上没有办法通过求导的方法来求这个对数似然函数的最大值。
　　MLE（极大似然估计）略显沮丧。这时候EM算法走过来，安慰着说：兄弟别哭，老哥帮你。

● 极大似然估计与EM算法适用问题分析

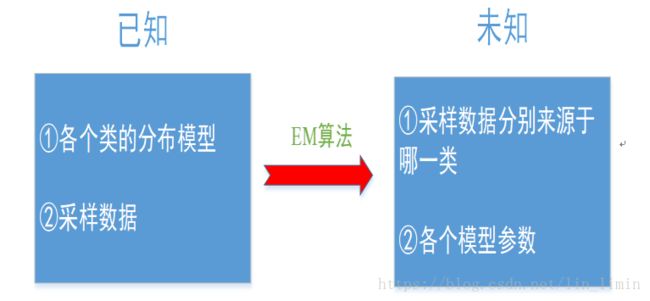
 　　下面先阐述一下极大似然估计与EM算法分别适用于解决什么样的问题。
　

图9 极大似然估计适用问题

图10 EM算法适用问题

 　　如果我们已经清楚了某个变量服从的高斯分布，而且通过采样得到了这个变量的样本数据，想求高斯分布的参数，这时候极大似然估计可以胜任这个任务；而如果我们要求解的是一个混合模型，只知道混合模型中各个类的分布模型（譬如都是高斯分布）和对应的采样数据，而不知道这些采样数据分别来源于哪一类（隐变量），那这时候就可以借鉴EM算法。EM算法可以用于解决数据缺失的参数估计问题（隐变量的存在实际上就是数据缺失问题，缺失了各个样本来源于哪一类的记录）。
　　下面将介绍EM算法的两个步骤：E-step(expectation-step，期望步)和M-step(Maximization-step,最大化步);

4.2 E-step

我们现有样本集$Y=(y_1,y_2...y_T)$，通过隐变量${\gamma }_{t,k}$（表示$y_t$这个样本来源于第k个模型）的引入，可以将数据展开成完全数据：
$$(y_t,{{\gamma }_t}_{,1},{\gamma }_{t,2}...{\gamma }_{t,K}),t=1,2...T$$

所谓的完全数据，就是不缺失的数据。只有样本集$Y=(y_1,y_2...y_T)$的数据是不完整的，存在信息缺失的。若$y_t$由第1类采样而来，则有${{\gamma }_t}_{,1}=1,{\gamma }_{t,2}=0...{\gamma }_{t,K}=0$，表示为$(y_t,1,0,...0)$。
　　所以要求能采到这组数据的可能性，需要分两步走：①第t个样本由哪一类产生？②如果第t个样本由第k类产生，那么第k类产生第t个样本的概率为多少？
　　综合考虑上面两步，有了完全数据的似然函数：
$$\begin{array}{l}p(y,\gamma |\mu ,\Sigma ,\pi )=\prod _{t=1}^{T}p(y_t,{{\gamma }_t}_{,1},{\gamma }_{t,2}...{\gamma }_{t,K}|\mu ,\Sigma ,\pi )\\ =\prod _{t=1}^T\prod _{k=1}^K{({\pi }_{k}N(y_t;{\mu }_k,{\Sigma }_k))}^{{\gamma }_{t,k}}\\ =\prod _{k=1}^K{\pi }_k^{{\sum }_{t=1}^T{}^{{\gamma }_{t,k}}}\prod _{t=1}^T{(N(y_t;{\mu }_k,{\Sigma }_k))}^{{\gamma }_{t,k}}\end{array}\text{\hspace{1em}(10)}$$
　　第1个等号到第2个等号的理解：若$y_t$由第1类采样而来，则有${{\gamma }_t}_{,1}=1,{\gamma }_{t,2}=0...{\gamma }_{t,K}=0$，
$$\begin{array}{l}p(y_t,{{\gamma }_t}_{,1},{\gamma }_{t,2}...{\gamma }_{t,K}|\mu ,\Sigma ,\pi )=\prod _{k=1}^K{({\pi }_{k}N(y_t;{\mu }_k,{\Sigma }_k))}^{{\gamma }_{t,k}}\\ =({\pi }_{1}N(y_t;{\mu }_1,{\Sigma }_1){)}^{{\gamma }_{t,1}}({\pi }_{2}N(y_t;{\mu }_2,{\Sigma }_2){)}^{{\gamma }_{t,2}}...({\pi }_{K}N(y_t;{\mu }_K,{\Sigma }_K){)}^{{\gamma }_{t,K}}\\ =({\pi }_{1}N(y_t;{\mu }_1,{\Sigma }_1){)}^1({\pi }_{2}N(y_t;{\mu }_2,{\Sigma }_2){)}^0...({\pi }_{K}N(y_t;{\mu }_K,{\Sigma }_K){)}^0\\ ={\pi }_{1}N(y_t;{\mu }_1,{\Sigma }_1)\end{array}\text{\hspace{1em}(11)}$$
　　注意式子(11)与式子(7)的差别：如果求$p(y_t)$则需要考虑$y_t$有可能来源于k个类；而如果求的是$p(y_t,{{\gamma }_t}_{,1},{\gamma }_{t,2}...{\gamma }_{t,K})$则已经限定了$y_t$只会来源于某个类。
　　第2个等式到第3个等式的理解：先交换累乘符号。由于${\pi }_k$与t无关，故而可以从内部的累乘符号中提取出来。
　　实际上完全数据的似然函数描述的就是采集到这些样本的可能性。
　　完全数据的对数似然函数为：
$$\ln p(y,\gamma |\mu ,\Sigma ,\pi )=\sum _{k=1}^K(\sum _{t=1}^T{\gamma }_{t,k})\ln {\pi }_k+\sum _{t=1}^T{\gamma }_{t,k}(-\ln (2\pi )-\frac{1}{2}\ln \left|{\Sigma }_k\right|-\frac{1}{2}(y_t-{\mu }_t{)}^T({\Sigma }_k{)}^{-1}(y_t-{\mu }_t))\text{\hspace{1em}(12)}$$
　　这一步应该没啥问题吧。。。注意的是，此处考虑的是二维高斯分布的情况，对应于式子(2)中的d=2。
　　我们的目标就是找出一组参数$(\mu \ast ,\Sigma \ast ,\pi \ast )$使得$\ln p(y,\gamma |\mu ,\Sigma ,\pi )$最大。
　　那么问题来了：$\ln p(y,\gamma |\mu ,\Sigma ,\pi )$中含有隐变量$\gamma$，$\gamma$的存在使得我们没法最大化$\ln p(y,\gamma |\mu ,\Sigma ,\pi )$ 。如果我们知道了$\gamma$，那么最大化$\ln p(y,\gamma |\mu ,\Sigma ,\pi )$就显得水到渠成。
　　但是坑爹的就是：我们只有采样数据$y_t$，$\gamma$未知。
　　那么怎么办呢？对$\gamma$来一个估计。
　　猜想我们给了一组起始参数$({\mu }^0,{\Sigma }^0,{\pi }^0)$或者优化过的第i次迭代的参数$({\mu }^i,{\Sigma }^i,{\pi }^i)$，也就是说每一个高斯分布的参数我们都有了，$\gamma$做的事不就是决定每个样本由哪一个高斯分布产生的嘛，有了每个高斯分布的参数那我们就可以猜想每个样本最有可能来源于哪个高斯分布没错吧！Done!
　　为此我们不最大化$\ln p(y,\gamma |\mu ,\Sigma ,\pi )$（也无法最大化它），而是最大化Q函数。Q函数如下：
$$\begin{array}{l}Q(\mu ,\Sigma ,\pi ,{\mu }^i,{\Sigma }^i,{\pi }^i)=E_{\gamma }[\ln p(y,\gamma |\mu ,\Sigma ,\pi )|Y,{\mu }^i,{\Sigma }^i,{\pi }^i]\\ =E_{\gamma }[\sum _{k=1}^K(\sum _{t=1}^T{\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)\ln {\pi }_k+\sum _{t=1}^T({\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)(-\ln (2\pi )-\frac{1}{2}\ln \left|{\Sigma }_k\right|-\frac{1}{2}(y_t-{\mu }_t{)}^T({\Sigma }_k{)}^{-1}(y_t-{\mu }_t))]\\ =\sum _{k=1}^K(\sum _{t=1}^{T}E({\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)\ln {\pi }_k+\sum _{t=1}^{T}E({\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)(-\ln (2\pi )-\frac{1}{2}\ln \left|{\Sigma }_k\right|-\frac{1}{2}(y_t-{\mu }_t{)}^T({\Sigma }_k{)}^{-1}(y_t-{\mu }_t)))\end{array}$$
　　其中，$E({\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)$就是对$\gamma$的估计：
$$\begin{array}{l}E({\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)=p({\gamma }_{t,k}=1|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)\\ =\frac{p({\gamma }_{t,k}=1,y_t|{\mu }^i,{\Sigma }^i,{\pi }^i)}{p(y_t)}\\ =\frac{p({\gamma }_{t,k}=1,y_t|{\mu }^i,{\Sigma }^i,{\pi }^i)}{{\sum }_{k=1}^{K}p({\gamma }_{t,k}=1,y_t|{\mu }^i,{\Sigma }^i,{\pi }^i)}\\ =\frac{p(y_t|{\gamma }_{t,k}=1,{\mu }^i,{\Sigma }^i,{\pi }^i)p({\gamma }_{t,k}=1|{\mu }^i,{\Sigma }^i,{\pi }^i)}{{\sum }_{k=1}^{K}p(y_t|{\gamma }_{t,k}=1,{\mu }^i,{\Sigma }^i,{\pi }^i)p({\gamma }_{t,k}=1|{\mu }^i,{\Sigma }^i,{\pi }^i)}\\ =\frac{{\pi }_k^{i}N(y_t;{\mu }_k^i,{\Sigma }_k^i)}{{\sum }_{k=1}^K{\pi }_k^{i}N(y_t;{\mu }_k^i,{\Sigma }_k^i)}\end{array}\text{\hspace{1em}(14)}$$
　　这公式是不是很可怕？？别急，带上几点声明，再去看公式就很好理解了！
　　① Q函数描述的其实就是在给定$({\mu }^i,{\Sigma }^i,{\pi }^i)$参数下，先对样本Y做一个最有可能的划分（每个样本来源于各个类的可能性，即对$\gamma$的估计$E({\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)$），再描述能够产生这组样本的可能性（Q函数）；
　　② 有了对于$\gamma$的估计之后，Q函数只和样本有关（传统意义上的似然函数亦如此，完全数据的似然函数还与$\gamma$有关），而不再含有隐变量，从而使得最大化Q函数成为可能；
　　③ 最大化Q函数的过程实则就是使得能够产生这组样本的可能性最大，与最大化似然函数的思路如出一辙。

4.3 M-step

有个Q函数，就可以对Q函数进行最大化，得到下一次迭代的模型参数了，即：
$${\mu }^{i+1},{\Sigma }^{i+1},{\pi }^{i+1}=\arg \max Q(\mu ,\Sigma ,\pi ,{\mu }^i,{\Sigma }^i,{\pi }^i)\text{\hspace{1em}(15)}$$
　　对Q函数进行求导，并另其导数为0，可得：
$${\mu }_k^{i+1}=\frac{{\sum }_{t=1}^T\frac{{\pi }_k^{i}N(y_t;{\mu }_k^i,{\Sigma }_k^i)}{{\sum }_{k=1}^K{\pi }_k^{i}N(y_t;{\mu }_k^i,{\Sigma }_k^i)}{y}_t}{E({\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)},k=1,2...K\text{\hspace{1em}(16)}$$
$${\Sigma }_k^{i+1}=\frac{{\sum }_{t=1}^T\frac{{\pi }_k^{i}N(y_t;{\mu }_k^i,{\Sigma }_k^i)}{{\sum }_{k=1}^K{\pi }_k^{i}N(y_t;{\mu }_k^i,{\Sigma }_k^i)}{(y_t-{\mu }_k^i)}^2}{E({\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)},k=1,2...K\text{\hspace{1em}(17)}$$
$${\pi }_k^{i+1}=\frac{E({\gamma }_{t,k}|y_t,{\mu }^i,{\Sigma }^i,{\pi }^i)}{T},k=1,2...K\text{\hspace{1em}(18)}$$
　　其中${\mu }_k^{i+1},{\Sigma }_k^{i+1},{\pi }_k^{i+1}$分别表示第（i+1）次迭代，第k个类的均值，协方差矩阵和所占的权重。

4.4 一个例子梳理EM算法的整个过程

 　　EM算法的核心思想是：通过迭代的过程来找到一组最优的参数$(\mu \ast ,\Sigma \ast ,\pi \ast )$，使得这组参数表示的模型最有可能产生现有的采样数据。每次迭代的过程就是参数矫正的过程。
　

图11 EM算法参数优化过程

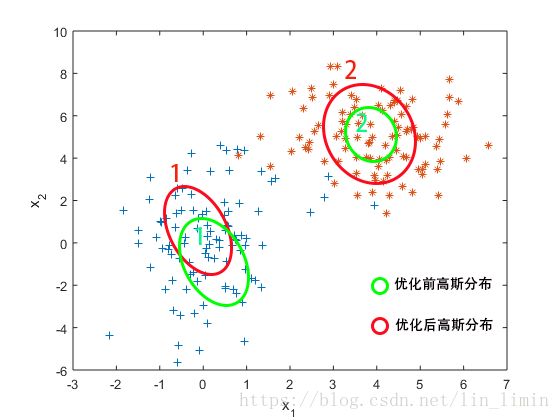
 　　现假设初始化一组参数$({\mu }^0,{\Sigma }^0,{\pi }^0)$。在这组参数下，2类二维高斯分布如图11绿色椭圆所示。然后利用现有的参数，E-step开始对样本数据进行划分（对$\gamma$进行估计）。蓝色的样本大多都被划分给第1类模型，橘黄色的样本大多都被划分给第2类模型。但是第1类模型还有优化空间：第1类模型还不能使得蓝色样本出现的联合概率达到最大。第2类模型也是如此。M-step便优化了2类模型的参数，得到新的参数$({\mu }^1,{\Sigma }^1,{\pi }^1)$，使得优化后2类高斯分布如图11红色椭圆所示。其中，第1类模型主要优化的是模型均值（即椭圆的中心），第二类模型主要优化的是模型协方差矩阵（即椭圆的长轴、短轴和长短轴的方向）。然后重复进行E-step和M-step，直到参数$(\mu ,\Sigma ,\pi )$收敛。
　　最后谈谈混合高斯模型的参数$\pi$。
　　混合高斯模型的参数$\mu ,\Sigma$比较好理解，用于描述各个高斯分布的形状，对于它们的调整也比较直观：使得本高斯分布能够更好地接纳被划分到这类分布的样本。而为什么要有参数$\pi$？它描述的是各个高斯分布所占的比重，如果不加“歧视”的话（样本来源于各个高斯分布的可能性一致），则有${\pi }_k=1/K$；而如果对于某一类高斯分布（即为i）有侧重的话，则相应的${\pi }_i$较大，体现在图11中就是被分配给各个类的样本数占样本总数的比例。如果一轮优化后，某一类高斯分布又接纳了更多样本，则其${\pi }_i$变大，反之变小（所以图11从绿色椭圆调整为红色椭圆实际上两个类所对应的权重也被优化了）。
　　而从本质上来看参数$\pi$，则是为了混合高斯模型能有更好的曲面拟合能力。当参数$\pi$退化为某一类高斯分布的权重远远大于其他类高斯分布的时候，混合高斯模型就退化成了单高斯模型！

5 总结

 　　图12和图13梳理了高斯分布和混合高斯分布参数估计的逻辑流程。
　

图12 高斯分布参数估计逻辑流程

图13 混合高斯分布参数估计逻辑流程

 　　相对比于高斯分布的参数估计，混合高斯分布的参数估计更加复杂。主要原因在于隐变量的存在。而为什么混合高斯分布的参数估计需要多次迭代循环进行？是因为EM算法中对于$\gamma$的估计利用的是初始化或者第i步迭代的参数$({\mu }^i,{\Sigma }^i,{\pi }^i)$，这对于样本的分类划分是有误差的。所以它只能通过多次迭代优化寻找更佳的参数来抵消这一误差。
　　终于把这篇文章梳理完了。世界杯要结束了，伪球迷也想见证一下冠军诞生。至此，本文结束。