摒弃encoder-decoder结构，Pervasive Attention模型与Keras实现
1.引言
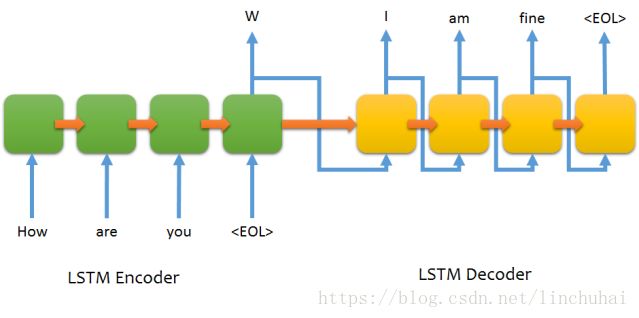
现有的主流机器翻译模型，基本都是基于encoder-decoder的结构，其思想就是对于输入句子序列，通过RNN先进行编码（encoder），转化为一个上下文向量context vector，然后利用另一个RNN对上下文向量context vector进行解码（decoder）。其结构如下：
之后，又有学者在该结构的基础上，做了各种改进，其中主要有两方面的改进，一种是添加了注意力机制，其思想就是在decoder的每一步输出时，不再仅仅关注encoder最后的输出状态，而是综合encoder每一个时间步的输出状态，并对其进行加权求和，从而使得在decoder的每一个时间步输出时，可以对输入句子序列中的个别词汇有所侧重，进而提高模型的准确率，另一种改进是替换encoder和decoder的RNN模型，比如Facebook提出的Fairseq模型，该模型在encoder和decoder都采用卷积神经网络模型，以及Googlet提出的Transformer模型，该模型在encoder和decoder都采用attention，这两种模型的出发点都是为了解决RNN没法并行计算的缺点，因此，在训练速度上得到了很大的提升。但是，这些改进其实都没有脱离encoder-decoder的结构。
因此，《Pervasive Attention: 2D Convolutional Neural Networks for Sequence-to-Sequence Prediction》一文作者提出了一种新的结构，不再使用encoder-decoder的结构，而是采用一种基于2D卷积神经网络（2D CNN）的结构，其思想就是将输入序列和目标序列embedding之后的矩阵进行拼接，转化为一个3D的矩阵，然后直接使用卷积网络进行卷积操作，其卷积网络的结构采用的是DenseNet的结构，并且在进行卷积时对卷积核进行遮掩，以防止在卷积时后续信息的流入，拼接后的feature map如下图所示：
2.相关符号定义
论文中涉及到的相关符号及其定义分别如下：
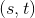：输入序列和目标序列句子对
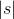：输入序列长度
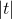：目标序列长度
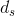：输入序列embedding的维度
：目标序列embedding的维度
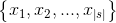：已经经过embedding的输入序列矩阵
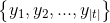：已经经过embedding的目标序列矩阵
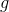：growth rate，与DenseNet中的growth rate含义相同，是每个dense layer的输出维度
3. pervasive attention模型介绍
pervasive attention模型的结构主要还是借鉴DenseNet的结构，在结构方面其实并没有多新奇，其主要特别的地方是将输入序列和目标序列的数据进行融合，转化为一个3D的矩阵，从而可以避开encoder-decoder的结构，下面对该模型具体展开介绍。
3.1 模型的输入（Input source-target tensor）
首先是模型的输入，记和分别表示输入序列和目标序列经过embedding后的二维矩阵，其中表示输入序列的长度，表示目标序列的长度，表示输入序列embedding后的维度，表示目标序列embedding后的维度。接着，将这两个矩阵进行拼接，得到一个三维的矩阵，记为
，其中
，![X_i_j=[y_i, x_j]](http://img.e-com-net.com/image/info8/f0155ca1ee7f40bf851ade4462f7bae6.gif){kind=small}
。这里有一个地方需要注意的是，作者在论文中是将数据转化为
的形式，这时，在后面的卷积操作时，卷积核的mask就应该是对行方向进行mask，而不是上图显示的列方向。
另外，笔者在查看作者源代码时，发现其实在将数据进行拼接之前，作者其实还做了一个conv embedding的操作，即对embedding后的输入序列和输出序列矩阵进行1维的卷积操作，这样使得后面每个单词其实都可以融合前一个单词的信息。
3.2 卷积层（Convolutional layers）
该论文中卷积层的结构主要参考的DenseNet的dense block结构，在每一个卷积block中，都包含以下7层：
- Batch_normalizes：第一层标准化层，对输入数据进行batch标准化
- ReLU：第一层激活层
- Conv(1)：第一层卷积层，采用(1,1)的卷积核，输入的通道数是
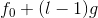，其中，
表示当前的层数，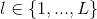
，
为dense layer的层数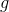，称作growth rate。因为采用的是DenseNet的结构，因此，需要将当前层前面的
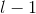层的输出作为附加的通道数与Input一起拼接。第一层卷积操作后的输出通道数设置为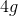
- Batch_normalizes：第二层标准化层
- ReLU：第二层激活层
- Conv(k)：第二层卷积层，采用
的卷积核，输出通道数是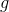 - dropout：dropout层
具体的模型结构如下图所示：
不过需要注意的是，笔者在查看作者源代码时，发现其实在最开始的Input与dense layer之间，其实还有一层DenseNet的transition操作，即对输入数据进行卷积，使得通道数减半，这样在后续的卷积操作时，数据量不会太大。
3.3 输出层（Target sequence prediction）
卷积层结束后，记模型的输出为
，其中
为输出的通道数，由于输出的是一个3维的结构，因此，需要对第2维进行折叠，使其转化为
的形式，这里作者介绍了两种主要的操作方法，分别是pooling和注意力机制：
- pooling：可以选择max_pooling或average_pooling，其计算方式分别如下：
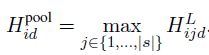
这里主要需要注意的是做average_pooling时，作者不是直接计算平均，而是除以句子长度的开根号，作者通过实验发现这种做法效果更好，并且作者在实验时发现用max_pooling效果要比average_pooling好。 - 注意力机制：与传统的注意力机制一样操作，这里不具体展开细讲了
得到折叠后的结果后，再将结果传入一个全连接层，使得输出的size转化为 
，这里
是目标序列的词汇总数，并将结果传入一个softmax层即可得到最终的概率分布，计算如下：
4.pervasive attention的keras实现
笔者用keras框架对pervasive attention进行了复现，下面对主要的代码模块按照上面介绍的模型结构进行讲解。首先导入相关的依赖库和函数。代码如下：
from keras.layers import Input, Embedding, \
Lambda, Concatenate, BatchNormalization, \
Conv2D, Dropout, Dense, MaxPool2D, ZeroPadding2D, \
AveragePooling2D, ZeroPadding1D
from keras.layers import Activation, TimeDistributed, Conv1D
from keras.models import Model
import keras.backend as K
from keras import optimizers 接着是模型的Input中的embedding部分，其中max_enc_len表示输入序列的最大长度，max_dec_len表示目标序列的最大长度，src_word_num表示输入序列的词汇数，tgt_word_num表示目标序列的词汇数，这里+2是为了添加
# Inputs
src_input = Input(shape=(max_enc_len,), name='src_input')
tgt_input = Input(shape=(max_dec_len,), name='tgt_input')
# embedding
src_embedding = Embedding(src_word_num + 2,
embedding_dim,
name='src_embedding')(src_input)
tgt_embedding = Embedding(tgt_word_num + 2,
embedding_dim,
name='tgt_embedding')(tgt_input)
# implement a convEmbedding
for i in range(conv_emb_layers):
src_embedding = Conv1D(embedding_dim, 3, padding='same',
data_format='channels_last', activation='relu')(src_embedding)
tgt_embedding = ZeroPadding1D(padding=(2, 0))(tgt_embedding)
tgt_embedding = Conv1D(embedding_dim, 3, padding='valid',
data_format='channels_last', activation='relu')(tgt_embedding) 然后对embedding之后的数据进行拼接，使其转化为一个3D的结构，这里笔者的代码与作者有点不一样的地方是将数据转化为
的形式，这样方便后面的卷积mask操作，本质上是一样的。
def src_reshape_func(src_embedding, repeat):
"""
对embedding之后的source sentence的tensor转换成pervasive-attention model需要的shape
arxiv.org/pdf/1808.03867.pdf
:param src_embedding: source sentence embedding之后的结果[tensor]
:param repeat: 需要重复的次数, target sentence t的长度[int]
:return: 2D tensor (?, s, t, embedding_dim)
"""
input_shape = src_embedding.shape
src_embedding = K.reshape(src_embedding, [-1, 1, input_shape[-1]])
src_embedding = K.tile(src_embedding, [1, repeat, 1])
src_embedding = K.reshape(src_embedding, [-1, input_shape[1], repeat, input_shape[-1]])
return src_embedding
def tgt_reshape_func(tgt_embedding, repeat):
"""
对embedding之后的target sentence的tensor转换成pervasive-attention model需要的shape
arxiv.org/pdf/1808.03867.pdf
:param tgt_embedding: target sentence embedding之后的结果[tensor]
:param repeat: 需要重复的次数, source sentence s的长度[int]
:return: 2D tensor (?, s, t, embedding_dim)
"""
input_shape = tgt_embedding.shape
tgt_embedding = K.reshape(tgt_embedding, [-1, 1, input_shape[-1]])
tgt_embedding = K.tile(tgt_embedding, [1, repeat, 1])
tgt_embedding = K.reshape(tgt_embedding, [-1, input_shape[1], repeat, input_shape[-1]])
tgt_embedding = K.permute_dimensions(tgt_embedding, [0, 2, 1, 3])
return tgt_embedding
def src_embedding_layer(src_embedding, repeat):
"""
转换成Lambda层
:param src_embedding: source sentence embedding之后的结果[tensor]
:param repeat: 需要重复的次数, target sentence t的长度[int]
:return: 2D tensor (?, s, t, embedding_dim)
"""
return Lambda(src_reshape_func,
arguments={'repeat': repeat})(src_embedding)
def tgt_embedding_layer(tgt_embedding, repeat):
"""
转换层Lambda层
:param tgt_embedding: target sentence embedding之后的结果[tensor]
:param repeat: 需要重复的次数, target sentence t的长度[int]
:return: 2D tensor (?, s, t, embedding_dim)
"""
return Lambda(tgt_reshape_func,
arguments={'repeat': repeat})(tgt_embedding)
# concatenate
src_embedding = src_embedding_layer(src_embedding, repeat=max_dec_len)
tgt_embedding = tgt_embedding_layer(tgt_embedding, repeat=max_enc_len)
src_tgt_embedding = Concatenate(axis=3)([src_embedding, tgt_embedding])拼接操作后， 为了避免后续卷积时数据太大，并且预测过多地依赖模型的初始信息，先将数据进行一次卷积操作，使得数据的通道数减半，这里conv2_filters即为卷积后的通道数，笔者设为原数据embedding维度大小。
# densenet conv1 1x1
x = Conv2D(conv1_filters, 1, strides=1)(src_tgt_embedding)
x = BatchNormalization(axis=3, epsilon=1.001e-5)(x)
x = Activation('relu')(x)
x = MaxPool2D((2, 1), strides=(2, 1))(x)
接下来是模型的卷积层部分，采用的是DenseNet的结构，由于句子比较长，因此，笔者在transition函数里做了一点修改，即每次transition操作对输入序列的维度进行降维，采用的是pooling操作，使得每次输入序列的维度可以不断下降，而更多的空间给通道数的增加，这里transition操作是一个可选操作，作者在论文中没讲，但是DenseNet原始的结构是有这一个操作的。另外，在卷积操作时，原作者是对卷积核的权重进行mask，比如卷积核为
时，直接对最后一列变为0，从而保证非法信息不会被传入，但是这里笔者直接采用
的卷积核，并对数据进行左padding两列，这样就不用重写卷积层了。
# transition layer
def transition_block(x,
reduction):
"""A transition block.
该transition block与densenet的标准操作不一样，此处不包括pooling层
pervasive-attention model中的transition layer需要保持输入tensor
的shape不变 arxiv.org/pdf/1808.03867.pdf
# Arguments
x: input tensor.
reduction: float, the rate of feature maps need to retain.
# Returns
output tensor for the block.
"""
x = BatchNormalization(axis=3, epsilon=1.001e-5)(x)
x = Activation('relu')(x)
x = Conv2D(int(K.int_shape(x)[3] * reduction), 1, use_bias=False)(x)
x = MaxPool2D((2, 1), strides=(2, 1))(x)
return x
# building block
def conv_block(x,
growth_rate,
dropout):
"""A building block for a dense block.
该conv block与densenet的标准操作不一样，此处通过
增加Zeropadding2D层实现论文中的mask操作，并将
Conv2D的kernel size设置为(3, 2)
# Arguments
x: input tensor.
growth_rate: float, growth rate at dense layers.
dropout: float, dropout rate at dense layers.
# Returns
Output tensor for the block.
"""
x1 = BatchNormalization(axis=3,
epsilon=1.001e-5)(x)
x1 = Activation('relu')(x1)
x1 = Conv2D(4 * growth_rate, 1, use_bias=False)(x1)
x1 = BatchNormalization(axis=3, epsilon=1.001e-5)(x1)
x1 = Activation('relu')(x1)
x1 = ZeroPadding2D(padding=((1, 1), (1, 0)))(x1) # mask sake
x1 = Conv2D(growth_rate, (3, 2), padding='valid')(x1)
x1 = Dropout(rate=dropout)(x1)
x = Concatenate(axis=3)([x, x1])
return x
# dense block
def dense_block(x,
blocks,
growth_rate,
dropout):
"""A dense block.
# Arguments
x: input tensor.
blocks: integer, the number of building blocks.
growth_rate:float, growth rate at dense layers.
dropout: float, dropout rate at dense layers.
# Returns
output tensor for the block.
"""
for i in range(blocks):
x = conv_block(x, growth_rate=growth_rate, dropout=dropout)
return x
# densenet 4 dense block
if len(blocks) == 1:
x = dense_block(x, blocks=blocks[-1], growth_rate=growth_rate, dropout=dropout)
else:
for i in range(len(blocks) - 1):
x = dense_block(x, blocks=blocks[i], growth_rate=growth_rate, dropout=dropout)
x = transition_block(x, reduction)
x = dense_block(x, blocks=blocks[-1], growth_rate=growth_rate, dropout=dropout)卷积操作结束后，是模型的pooling操作，对s维度进行折叠，这里笔者只写了pooling操作。
# avg pooling
def h_avg_pooling_layer(h):
"""
实现论文中提到的均值池化 arxiv.org/pdf/1808.03867.pdf
:param h: 由densenet结构输出的shape为(?, s, t, fl)的tensor[tensor]
:return: (?, t, fl)
"""
h = Lambda(lambda x: K.permute_dimensions(x, [0, 2, 1, 3]))(h)
h = AveragePooling2D(data_format='channels_first',
pool_size=(h.shape[2], 1))(h)
h = Lambda(lambda x: K.squeeze(x, axis=2))(h)
return h
# max pooling
def h_max_pooling_layer(h):
"""
实现论文中提到的最大池化 arxiv.org/pdf/1808.03867.pdf
:param h: 由densenet结构输出的shape为(?, s, t, fl)的tensor[tensor]
:return: (?, t, fl)
"""
h = Lambda(lambda x: K.permute_dimensions(x, [0, 2, 1, 3]))(h)
h = MaxPool2D(data_format='channels_first',
pool_size=(h.shape[2], 1))(h)
h = Lambda(lambda x: K.squeeze(x, axis=2))(h)
return h
# Max pooling
h = h_max_pooling_layer(x)最后是模型的输出，是一个全连接层+softmax层，这里没什么好讲的，代码如下：
# Max pooling
h = h_max_pooling_layer(x)
# Target sequence prediction
output = Dense(tgt_word_num + 2, activation='softmax')(h)以上对整个模型各个模块代码分别进行了讲解，最后，将上面的代码串联起来，汇总如下：
# pervasive-attention model
def pervasive_attention(blocks,
conv1_filters=64,
growth_rate=12,
reduction=0.5,
dropout=0.2,
max_enc_len=200,
max_dec_len=200,
embedding_dim=128,
src_word_num=4000,
tgt_word_num=4000,
samples=12000,
batch_size=8,
conv_emb_layers=6
):
"""
build a pervasive-attention model with a densenet-like cnn structure.
:param blocks: a list with length 4, indicates different number of
building blocks in 4 dense blocks, e.g which [6, 12, 48, 32]
for DenseNet201 and [6, 12, 32, 32] for DenseNet169. [list]
:param conv1_filters: the filters used in first 1x1 conv to
reduce the channel size of embedding input. [int]
:param growth_rate: float, growth rate at dense layers. [int]
:param reduction: float, the rate of feature maps which
need to retain after transition layer. [float]
:param dropout: dropout rate used in each conv block, default 0.2. [float]
:param max_enc_len: the max len of source sentences. [int]
:param max_dec_len: the max len of target sentences. [int]
:param embedding_dim: the hidden units of first two embedding layers. [int]
:param src_word_num: the vocabulary size of source sentences. [int]
:param tgt_word_num: the vocabulary size of target sentences. [int]
:param samples: the size of the training data. [int]
:param batch_size: batch size. [int]
:param conv_emb_layers: the layers of the convolution embedding. [int]
:return:
"""
# Inputs
src_input = Input(shape=(max_enc_len,), name='src_input')
tgt_input = Input(shape=(max_dec_len,), name='tgt_input')
# embedding
src_embedding = Embedding(src_word_num + 2,
embedding_dim,
name='src_embedding')(src_input)
tgt_embedding = Embedding(tgt_word_num + 2,
embedding_dim,
name='tgt_embedding')(tgt_input)
# implement a convEmbedding
for i in range(conv_emb_layers):
src_embedding = Conv1D(embedding_dim, 3, padding='same',
data_format='channels_last', activation='relu')(src_embedding)
tgt_embedding = ZeroPadding1D(padding=(2, 0))(tgt_embedding)
tgt_embedding = Conv1D(embedding_dim, 3, padding='valid',
data_format='channels_last', activation='relu')(tgt_embedding)
# concatenate
src_embedding = src_embedding_layer(src_embedding, repeat=max_dec_len)
tgt_embedding = tgt_embedding_layer(tgt_embedding, repeat=max_enc_len)
src_tgt_embedding = Concatenate(axis=3)([src_embedding, tgt_embedding])
# densenet conv1 1x1
x = Conv2D(conv1_filters, 1, strides=1)(src_tgt_embedding)
x = BatchNormalization(axis=3, epsilon=1.001e-5)(x)
x = Activation('relu')(x)
x = MaxPool2D((2, 1), strides=(2, 1))(x)
# densenet 4 dense block
if len(blocks) == 1:
x = dense_block(x, blocks=blocks[-1], growth_rate=growth_rate, dropout=dropout)
else:
for i in range(len(blocks) - 1):
x = dense_block(x, blocks=blocks[i], growth_rate=growth_rate, dropout=dropout)
x = transition_block(x, reduction)
x = dense_block(x, blocks=blocks[-1], growth_rate=growth_rate, dropout=dropout)
# Max pooling
h = h_max_pooling_layer(x)
# Target sequence prediction
output = Dense(tgt_word_num + 2, activation='softmax')(h)
# compile
model = Model([src_input, tgt_input], [output])
adam = optimizers.Adam(lr=0.0001,
beta_1=0.9,
beta_2=0.999,
epsilon=1e-08,
decay=0.05 * batch_size / samples)
model.compile(optimizer=adam, loss='categorical_crossentropy')
return model5.小结
以上就是pervasive attention模型的整体结构及其复现，其实整个模型的思路都不算太难，下面谈一谈笔者自己对这个模型的一个感受吧：
- 优点：①抛弃了以往的encoder和decoder结构，可以直接采用卷积操作进行计算，从而实现并行化；②参数量整体比seq2seq要少很多；③可以在每一层的结果实现attention，这也是模型为什么叫pervasive attention的原因。
- 缺点：该模型由于对输入序列和目标序列的数据进行拼接，当序列的长度比较长时，对GPU的内存要求就很高，特别是当层数和growth rate比较大时，对GPU的性能要求就特别大。
最后，附上原论文的地址和作者源代码的地址：
- 论文地址：arxiv.org/pdf/1808.03867.pdf
- Pytorch实现：github.com/elbayadm/attn2d
招聘信息：
熊猫书院算法工程师：
https://www.lagou.com/jobs/4842081.html
希望对深度学习算法感兴趣的小伙伴们可以加入我们，一起改变教育！