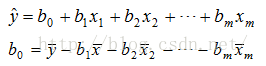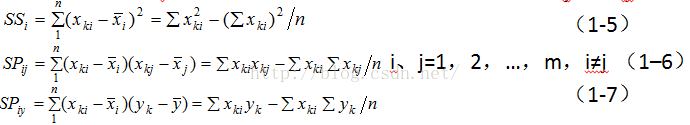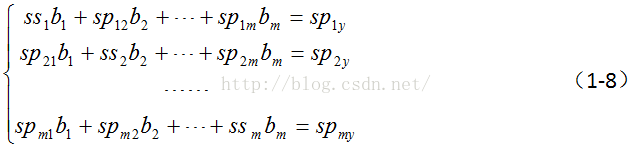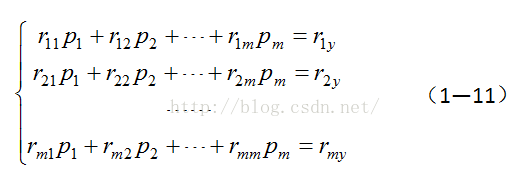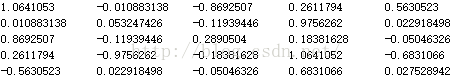逐步回归算法java实现
逐步回归在维基百科上有这样的定义: Stepwise regression includes regression models in which the choice of predictive variables is carried out by an automatic procedure.也就是能自动地选取合适的变量来建立回归方程。所以我认为逐步回归与其说是一种回归方法,不如说是一种回归辅助手段,是帮助线性回归,非线性回归或其他回归方法确定最优回归方程的方法。所以其核心内容有2点:
1.根本目的是确定最优回归方程。2.关键内容:变量选择。
对于变量选择有三种常见方法:
1.Forward selection 向前选择法。即一个一个得将变量加入回归方程中。这种方法的缺点在于它不能反映后来变化的情况。因为对于某个自变量,它可能开始是显著的,即将其引入到回归方程,但是,随着以后其他自变量的引入,它也可能又变为不显著了,但是,并没有将其及时从回归方程中剔除掉。也就是增加变量法,只考虑引入而不考虑剔除。
2.Backward elimination 向后消去法。即先将全部变量加入回归方程,然后根据选择标准逐一剔除。这种方法的缺点在于一开始把全部变量都引入回归方程,这样计算量比较大。若对一些不重要的变量,一开始就不引入,这样就可以减少一些计算。
3.Bidirectional elimination 逐步筛选法。这种方法是前两种方法的结合,是在引入新的变量的时候考虑是否要剔除因为引入这个变量使得先前引入的变量显得不重要。
有了变量选择的方法,下面就要选择合适的选择标准。其中最常用的是F检验,也是本文后面讲解算法所使用的方法。其余的还有R-square,Akaike information criterion(AIC),Bayesian information criterion等等方法。使用R语言实现的逐步回归方法就是使用得AIC标准,来判断其过拟合程度,AIC越小,过拟合程度越低。
下面用一个具体的例子来一步一步讲解逐步回归的算法:
例1 某种水泥在凝固时放出的热量(卡/克)与水泥中下列四种化学成分有关:
: 的成分(%),
: 的成分(%),
: 的成分(%),
: 的成分(%)。
所测定数据如表1所示, 试建立与、、及的线性回归模型。
表1
| 试验序号 |
|
|
|
|
|
| 1 |
7 |
26 |
6 |
60 |
78.5 |
| 2 |
1 |
29 |
15 |
52 |
74.3 |
| 3 |
11 |
56 |
8 |
20 |
104.3 |
| 4 |
11 |
31 |
8 |
47 |
87.6 |
| 5 |
7 |
52 |
6 |
33 |
95.9 |
| 6 |
11 |
55 |
9 |
22 |
109.2 |
| 7 |
3 |
71 |
17 |
6 |
102.7 |
| 8 |
1 |
31 |
22 |
44 |
72.5 |
| 9 |
2 |
54 |
18 |
22 |
93.1 |
| 10 |
21 |
47 |
4 |
26 |
115.9 |
| 11 |
1 |
40 |
23 |
34 |
83.8 |
| 12 |
11 |
66 |
9 |
12 |
113.3 |
| 13 |
10 |
68 |
8 |
12 |
109.4 |
注: 本例子引自 中国科学院数学研究室数理统计组编,《回归分析方法》, 科学出版社, 1974年
一、计算相关系数矩阵
1.假设存在线性关系
2.计算各变量的平均数及标准差
3.计算离差阵
自变量平方和ssi,自变量间及其与因变量间的乘积和SPij及SPiy由下式算出:
这里可以理解成将表1中的各列数据减去各列的均值而形成的矩阵C,C的转置乘以C得到的矩阵。
于是可得正规方程组:
4.计算相关系数阵
rij为x1,x2,…,xm,y间的相关系数,且rii=1,于是正规方程组(1-8)可改写为:
针对本例计算得到的关系矩阵为:
方程组(1-12)中的pi与方程组(1-8)中bi间的关系为:
bi=piSy/Sxi i=1,2,…,m (1-13)
式中Sxi,Sy为各自变量、因变量的标准差。
二、确定显著的F检验水准
显著水准F的取值与自由度有关,而且在逐步回归的分析中,由于自变量引入和剔除的变化,其剩余自由度也在不断变化,若样本的观察数为n,自变量的个数为m,则剩余自由度为n-m-1。当n相对于m较大时,可确定一个固定的F检验值。在本例中显著性水平α=0.10,引入变量的临界值Fa=3.280,剔除变量的临界值Fe=3.280。
三、选取自变量
(1)对5个自变量计算偏回归平方和,各自变量的偏回归平方和ui为:
(2)对xi引入回归方程是否显著进行F检验
(3)剔除或引入一个自变量xk后,相关系数阵R(L)按下列公式进行消去变换,而成R(L+1)
引入第N个自变量方法相同。但是要判断之前的自变量是否要剔除。仍然采用F检验。
针对本例:第1步, 引入变量:
相关系数矩阵为:
各项的判别值(升序排列):
Vx(3)= 0.286
Vx(1)= 0.534
Vx(2)= 0.666
Vx(4)= 0.675
未引入项中, 第4项[X(4)]Vx值(≥0)的绝对值最大,
引入检验值Fa(4)=22.80, 引入临界值Fa=3.280,
Fa(4)>Fa, 引入第4项, 已引入项数=1。
进行消去变换得到相关系数矩阵为:
第2步, 引入变量:
各项的判别值(升序排列):
Vx(4)=-0.675
Vx(2)= 5.52e-3
Vx(3)= 0.261
Vx(1)= 0.298
未引入项中, 第1项[X(1)]Vx值(≥0)的绝对值最大,
引入检验值Fa(1)=108.2, 引入临界值Fa=3.280,
Fa(1)>Fa, 引入第1项, 已引入项数=2。
进行消去变换得到相关系数矩阵为:
第3步, 引入变量:
各项的判别值(升序排列):
Vx(4)=-0.439
Vx(1)=-0.298
Vx(3)= 8.81e-3
Vx(2)= 9.86e-3
未引入项中, 第2项[X(2)]Vx值(≥0)的绝对值最大,
引入检验值Fa(2)=5.026, 引入临界值Fa=3.280,
Fa(2)>Fa, 引入第2项, 已引入项数=3。
进行消去变换得到相关系数矩阵为:
第4步, 剔除或引入变量:
各项的判别值(升序排列):
Vx(1)=-0.302
Vx(2)=-9.86e-3
Vx(4)=-3.66e-3
Vx(3)= 4.02e-5
已引入项中, 第4项[X(4)]Vx值(<0)的绝对值最小,
未引入项中, 第3项[X(3)]Vx值(≥0)的绝对值最大,
剔除检验值Fe(4)=1.863, 剔除临界值Fe=3.280,
Fe(4)≤Fe, 剔除第4项, 已引入项数=2。
进行消去变换得到相关系数矩阵为:

第5步, 剔除或引入变量:
各项的判别值(升序排列):
Vx(2)=-0.445
Vx(1)=-0.312
Vx(3)= 3.61e-3
Vx(4)= 3.66e-3
已引入项中, 第1项[X(1)]Vx值(<0)的绝对值最小,
未引入项中, 第4项[X(4)]Vx值(≥0)的绝对值最大,
剔除检验值Fe(1)=146.5, 剔除临界值Fe=3.280,
Fe(1)>Fe, 不能剔除第1项。
引入检验值Fa(4)=1.863, 引入临界值Fa=3.280,
Fa(4)≤Fa, 不能引入第4项, 已引入项数=2。
回归结束。
四、建立最优回归方程
计算偏回归系数
得到回归方程为y=52.577347+1.4683057x1+0.6622506x2
计算复相关系数及回归方程估计标准误差
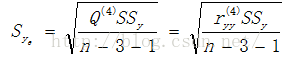
import java.util.ArrayList;
public class Stepwise {
public static void main(String[] args) throws Exception {
// TODO Auto-generated method stub
CsvUtil util = new CsvUtil("C:\\Users\\Yu Xin\\Desktop\\实验室项目\\逐步回归\\stepwise.csv");
int rowNum = util.getRowNum();//文件行数(包括标头)
int colNum = util.getColNum();//文件列数(包括序号列)
float[][] source=new float[rowNum-1][colNum-1];//文件中读取的数据矩阵
float[] mean=new float[colNum-1];//每列均值
float[] dev=new float[colNum-1];//每列方差
float[][] sp=new float[colNum-1][colNum-1];//离差阵
float[][] r=new float[colNum-1][colNum-1];//相关系数矩阵
ArrayList choose=new ArrayList();//被选中的自变量
for(int i=0;iF_out)){
choose.remove(min_index+"");
r=trans(r,min_index,colNum);
for(int i=0;iF_in){
choose.add(index+"");
r=trans(r,index,colNum);
for(int i=0;i=max){
index=i;
max=Math.abs(pu[i]);
}
}
return index;
}
public static int getMinIndex(float[] pu,ArrayList pchoose){
int index=0;
float min=1;
for(String in:pchoose){
int ii=Integer.parseInt(in);
if(Math.abs(pu[ii])<=min){
index=ii;
min=Math.abs(pu[ii]);
}
}
return index;
}
//消去变换
public static float[][] trans(float[][] pr,int pindex,int pcol){
float[][] r2=new float[pcol-1][pcol-1];
for(int i=0;i