手写卷积运算
最近看到一个巨牛的人工智能教程,分享一下给大家。教程不仅是零基础,通俗易懂,而且非常风趣幽默,像看小说一样!觉得太牛了,所以分享给大家。平时碎片时间可以当小说看,【点这里可以去膜拜一下大神的“小说”】。
从一个通道的图片进行卷积生成新的单通道图的过程很容易理解,对于多个通道卷积后生成多个通道的图理解起来有点抽象。本文以通俗易懂的方式讲述卷积,并辅以图片解释,能快速理解卷积的实现原理。最后手写python代码实现卷积过程,让Tensorflow卷积在我们面前不再是黑箱子!
注意:
本文只针对batch_size=1,padding=‘SAME’,stride=[1,1,1,1]进行实验和解释,其他如果不是这个参数设置,原理也是一样。
1 Tensorflow卷积实现原理
先看一下卷积实现原理,对于in_c个通道的输入图,如果需要经过卷积后输出out_c个通道图,那么总共需要in_c * out_c个卷积核参与运算。参考下图:
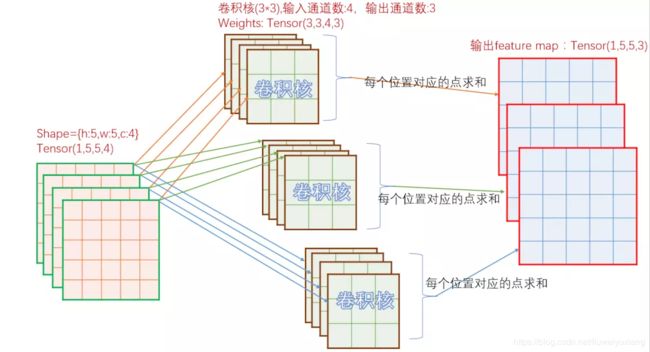
如上图,输入为[h:5,w:5,c:4],那么对应输出的每个通道,需要4个卷积核。上图中,输出为3个通道,所以总共需要3*4=12个卷积核。对于单个输出通道中的每个点,取值为对应的一组4个不同的卷积核经过卷积计算后的和。
接下来,我们以输入为2个通道宽高分别为5的输入、3*3的卷积核、1个通道宽高分别为5的输出,作为一个例子展开。
2个通道,5*5的输入定义如下:
#输入,shape=[c,h,w]
input_data=[
[[1,0,1,2,1],
[0,2,1,0,1],
[1,1,0,2,0],
[2,2,1,1,0],
[2,0,1,2,0]],
[[2,0,2,1,1],
[0,1,0,0,2],
[1,0,0,2,1],
[1,1,2,1,0],
[1,0,1,1,1]],
]
对于输出为1通道map,根据前面计算方法,需要2*1个卷积核。定义卷积核如下:
#卷积核,shape=[in_c,k,k]=[2,3,3]
weights_data=[
[[ 1, 0, 1],
[-1, 1, 0],
[ 0,-1, 0]],
[[-1, 0, 1],
[ 0, 0, 1],
[ 1, 1, 1]]
]
上面定义的数据,在接下来的计算对应关系将按下图所描述的方式进行。
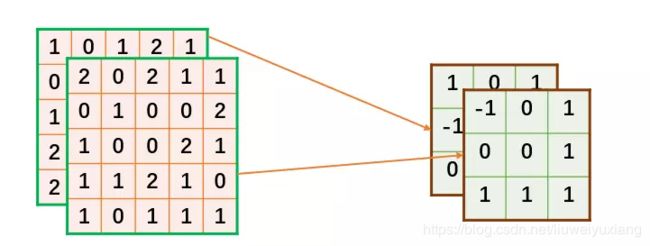
由于Tensorflow定义的tensor的shape为[n,h,w,c],这里我们可以直接把n设为1,即batch size为1。还有一个问题,就是我们刚才定义的输入为[c,h,w],所以需要将[c,h,w]转为[h,w,c]。转换方式如下,注释已经解释很详细,这里不再解释。
def get_shape(tensor):
[s1,s2,s3]= tensor.get_shape()
s1=int(s1)
s2=int(s2)
s3=int(s3)
return s1,s2,s3
def chw2hwc(chw_tensor):
[c,h,w]=get_shape(chw_tensor)
cols=[]
for i in range(c):
#每个通道里面的二维数组转为[w*h,1]即1列
line = tf.reshape(chw_tensor[i],[h*w,1])
cols.append(line)
#横向连接,即将所有竖直数组横向排列连接
input = tf.concat(cols,1)#[w*h,c]
#[w*h,c]-->[h,w,c]
input = tf.reshape(input,[h,w,c])
return input
同理,Tensorflow使用卷积核的时候,使用的格式是[k,k,in_c,out_c]。而我们在定义卷积核的时候,是按[in_c,k,k]的方式定义的,这里需要将[in_c,k,k]转为[k,k,in_c],由于为了简化工作量,我们规定输出为1个通道,即out_c=1。所以这里我们可以直接简单地对weights_data调用chw2hwc,再在第3维度扩充一下即可。
接下来,贴出完整的代码:
import tensorflow as tf
import numpy as np
input_data=[
[[1,0,1,2,1],
[0,2,1,0,1],
[1,1,0,2,0],
[2,2,1,1,0],
[2,0,1,2,0]],
[[2,0,2,1,1],
[0,1,0,0,2],
[1,0,0,2,1],
[1,1,2,1,0],
[1,0,1,1,1]],
]
weights_data=[
[[ 1, 0, 1],
[-1, 1, 0],
[ 0,-1, 0]],
[[-1, 0, 1],
[ 0, 0, 1],
[ 1, 1, 1]]
]
def get_shape(tensor):
[s1,s2,s3]= tensor.get_shape()
s1=int(s1)
s2=int(s2)
s3=int(s3)
return s1,s2,s3
def chw2hwc(chw_tensor):
[c,h,w]=get_shape(chw_tensor)
cols=[]
for i in range(c):
#每个通道里面的二维数组转为[w*h,1]即1列
line = tf.reshape(chw_tensor[i],[h*w,1])
cols.append(line)
#横向连接,即将所有竖直数组横向排列连接
input = tf.concat(cols,1)#[w*h,c]
#[w*h,c]-->[h,w,c]
input = tf.reshape(input,[h,w,c])
return input
def hwc2chw(hwc_tensor):
[h,w,c]=get_shape(hwc_tensor)
cs=[]
for i in range(c):
#[h,w]-->[1,h,w]
channel=tf.expand_dims(hwc_tensor[:,:,i],0)
cs.append(channel)
#[1,h,w]...[1,h,w]---->[c,h,w]
input = tf.concat(cs,0)#[c,h,w]
return input
def tf_conv2d(input,weights):
conv = tf.nn.conv2d(input, weights, strides=[1, 1, 1, 1], padding='SAME')
return conv
def main():
const_input = tf.constant(input_data , tf.float32)
const_weights = tf.constant(weights_data , tf.float32 )
input = tf.Variable(const_input,name="input")
#[2,5,5]------>[5,5,2]
input=chw2hwc(input)
#[5,5,2]------>[1,5,5,2]
input=tf.expand_dims(input,0)
weights = tf.Variable(const_weights,name="weights")
#[2,3,3]-->[3,3,2]
weights=chw2hwc(weights)
#[3,3,2]-->[3,3,2,1]
weights=tf.expand_dims(weights,3)
#[b,h,w,c]
conv=tf_conv2d(input,weights)
rs=hwc2chw(conv[0])
init=tf.global_variables_initializer()
sess=tf.Session()
sess.run(init)
conv_val = sess.run(rs)
print(conv_val[0])
if __name__=='__main__':
main()
上面代码有几个地方需要提一下,
- 由于输出通道为1,因此可以对卷积核数据转换的时候直接调用chw2hwc,如果输入通道不为1,则不能这样完成转换。
- 输入完成chw转hwc后,记得在第0维扩充维数,因为卷积要求输入为[n,h,w,c]
- 为了方便我们查看结果,记得将hwc的shape转为chw
执行上面代码,运行结果如下:
[[ 2. 0. 2. 4. 0.]
[ 1. 4. 4. 3. 5.]
[ 4. 3. 5. 9. -1.]
[ 3. 4. 6. 2. 1.]
[ 5. 3. 5. 1. -2.]]
这个计算结果是怎么计算出来的?为了让大家更清晰的学习其中细节,我特地制作了一个GIF图,看完这个图后,如果你还看不懂卷积的计算过程,你可以来打我。。。。
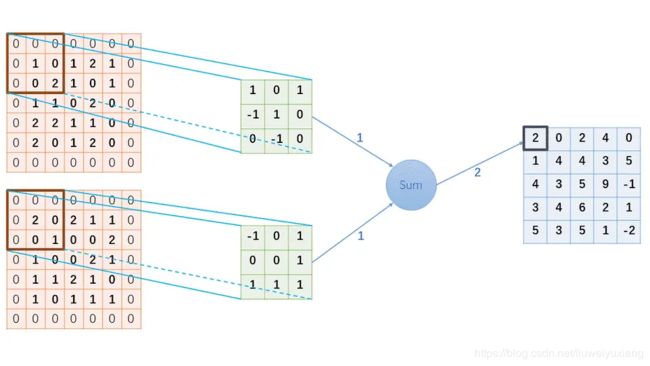
2 手写Python代码实现卷积
自己实现卷积时,就无须将定义的数据[c,h,w]转为[h,w,c]了。
import numpy as np
input_data=[
[[1,0,1,2,1],
[0,2,1,0,1],
[1,1,0,2,0],
[2,2,1,1,0],
[2,0,1,2,0]],
[[2,0,2,1,1],
[0,1,0,0,2],
[1,0,0,2,1],
[1,1,2,1,0],
[1,0,1,1,1]]
]
weights_data=[
[[ 1, 0, 1],
[-1, 1, 0],
[ 0,-1, 0]],
[[-1, 0, 1],
[ 0, 0, 1],
[ 1, 1, 1]]
]
#fm:[h,w]
#kernel:[k,k]
#return rs:[h,w]
def compute_conv(fm,kernel):
[h,w]=fm.shape
[k,_]=kernel.shape
r=int(k/2)
#定义边界填充0后的map
padding_fm=np.zeros([h+2,w+2],np.float32)
#保存计算结果
rs=np.zeros([h,w],np.float32)
#将输入在指定该区域赋值,即除了4个边界后,剩下的区域
padding_fm[1:h+1,1:w+1]=fm
#对每个点为中心的区域遍历
for i in range(1,h+1):
for j in range(1,w+1):
#取出当前点为中心的k*k区域
roi=padding_fm[i-r:i+r+1,j-r:j+r+1]
#计算当前点的卷积,对k*k个点点乘后求和
rs[i-1][j-1]=np.sum(roi*kernel)
return rs
def my_conv2d(input,weights):
[c,h,w]=input.shape
[_,k,_]=weights.shape
outputs=np.zeros([h,w],np.float32)
#对每个feature map遍历,从而对每个feature map进行卷积
for i in range(c):
#feature map==>[h,w]
f_map=input[i]
#kernel ==>[k,k]
w=weights[i]
rs =compute_conv(f_map,w)
outputs=outputs+rs
return outputs
def main():
#shape=[c,h,w]
input = np.asarray(input_data,np.float32)
#shape=[in_c,k,k]
weights = np.asarray(weights_data,np.float32)
rs=my_conv2d(input,weights)
print(rs)
if __name__=='__main__':
main()
代码无须太多解释,直接看注释。然后跑出来的结果如下:
[[ 2. 0. 2. 4. 0.]
[ 1. 4. 4. 3. 5.]
[ 4. 3. 5. 9. -1.]
[ 3. 4. 6. 2. 1.]
[ 5. 3. 5. 1. -2.]]
对比发现,跟Tensorflow的卷积结果是一样的。
3 小结
本文中,我们学习了Tensorflow的卷积实现原理,通过也通过python代码实现了输出通道为1的卷积,其实输出通道数不影响我们学习卷积原理。后面如果有机会的话,我们去实现一个更加健全,完整的卷积。
原文链接:Tensorflow卷积实现原理+手写python代码实现卷积